Methods to Reduce the Bit Error Rate in DSL

1. Examples of Communication Systems
2. DSL – Digital Subscriber Line
3. Methods to Reduce the Bit Error Rate in DSL

• Previous page
• Next page

• Previous page
• Next page

Transmission properties of copper cables

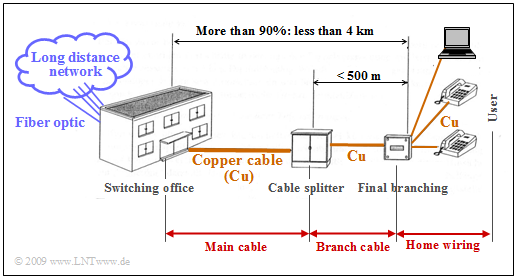
As already mentioned in the chapter  "General Description of DSL" , the telephone line network of Deutsche Telekom mainly uses balanced copper pairs with a diameter of  $\text{0.4 mm}$.  The  "last mile"  is divided into three segments:

• the main cable,

• the branch cable,

• the house connection cable.

On average,  the line length is less than four kilometers.  In cities,  the copper line is shorter than  $\text{2.8 km}$  in  $90\%$  of all cases.

Structure of the local loop area

The $\rm xDSL$ variants discussed here were developed specifically for use on such symmetrical balanced copper pairs in the cable network. In order to better understand the technical requirements for the xDSL systems, a closer look must be taken at the transmission characteristics and interference on the conductor pairs.

This topic has already been dealt with in detail in the fourth main chapter  "Properties of Electrical Lines"  of the book  "Linear and Time Invariant Systems"  and is therefore only briefly summarized here using the  "equivalent circuit diagram" :

• Line transmission properties are fully characterized by the generally complex

•   "characteristic impedance"  $Z_{\rm W}(f)$  and
•   "complex propagation function per unit length"   ⇒   $γ(f)$.

• The even  "attenuation function $($per unit length$)$"  $α(f)$  is the real part of  $γ(f)$  and describes the attenuation of the wave propagating along the line:

$$α(-f)=α(f) .$$

• The odd imaginary part  $β(f)$  of  $γ(f)$  is called  "phase function  $($per unit length$)$"  and gives the phase rotation of the signal wave along the line:

$$β(-f)=-β(f) .$$

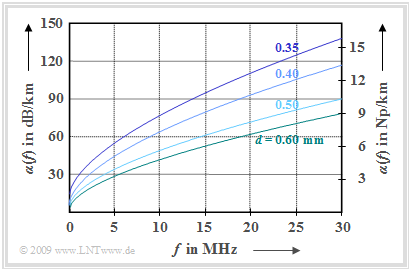
$\text{Example 1:}$  As an example,  we consider the function  $\alpha(f)$  shown on the right,  which is based on empirical investigations by  "Deutsche Telekom".

Attenuation function per unit length of balanced copper pairs

The curves were obtained by averaging over a large number of measured lines of one kilometer length in the frequency range up to  $\text{30 MHz}$.  One can see:

1. The attenuation function  $($per unit length$)$   $α(f)$  increases approximately proportionally with the square root of the frequency and decreases with increasing conductor diameter  $d$.
2. The attenuation function  $a(f)$  increases linearly with cable length  $l$:

$$a(f) = α(f) · l.$$

Note the difference between

• $a(f)$   speak "a"   $($for the attenuation function$)$,

• $\alpha(f)$   speak "a" $($for the attenuation function per unit length$)$.

For the line diameter  $\text{0.4 mm}$  was given in  [PW95]  an empirical approximation formula for the attenuation function per unit length:

$$\alpha(f) = \left [ 5.1 + 14.3 \cdot \left (\frac{f}{\rm 1\,MHz}\right )^{0.59} \right ] \frac{\rm dB}{\rm km} \hspace{0.05cm}.$$

Evaluating this equation,  the following exemplary values hold:

• The attenuation function  $a(f)$  of a balanced copper wire of length  $l = 1 \ \rm km$  with diameter  $0.4 \ \rm mm$  is slightly more than  $60\ \rm dB$  for the signal frequency  $10\ \rm MHz$.

• At twice the frequency  $(20 \ \rm MHz)$  the attenuation value increases to over  $90 \ \rm dB$.  It can be seen that the attenuation does not increase exactly with the root of the frequency,  as would be the case if the skin effect were considered alone,  since several other effects also contribute to the attenuation.

• If the cable length is doubled to   $l = 2 \ \rm km$   the attenuation reaches a value of more than  $120 \ \rm dB$  $($at  $10 \ \rm MHz)$,  which corresponds to an amplitude attenuation factor smaller than  $10^{-6}$.

• Due to the frequency dependence of   $α(f)$  and  $β(f)$:   »intersymbol interference«  $\rm (ISI)$  as well as  »intercarrier interference  $\rm (ICI)$  occur. 

• Suitable equalization must therefore be provided for xDSL.

Note:

1. In the  "Properties of balanced copper pairs"  chapter of the book  "Linear Time-Invariant Systems"  this topic is treated in detail.
2. We refer here to the interactive applet  "Attenuation of copper cables".

Disturbances during transmission

Every transmission system is affected by disturbances,  which usually results primarily from thermal resistance noise.  In addition,  for a two-wire line there are:

• »Reflections«:   The counter-propagating wave increases the attenuation of copper pairs,  which is taken into account in the  "operational attenuation"  of the line.  To prevent such reflection,  the terminating resistor  $Z_{\rm E}(f)$  would have to be chosen identical to the  $($complex and frequency-dependent$)$  characteristic impedance  $Z_{\rm W}(f)$.  This is difficult in practice.  Therefore,  the terminating resistors are chosen to be real and constant,  and the resulting reflections are combated by technical means  – if possible.

On the emergence of crosstalk

• »Crosstalk«:   This is dominant interference in conducted transmission. 
  Crosstalk occurs when inductive and capacitive couplings between adjacent cores of a cable bundle cause mutual interference during signal transmission.

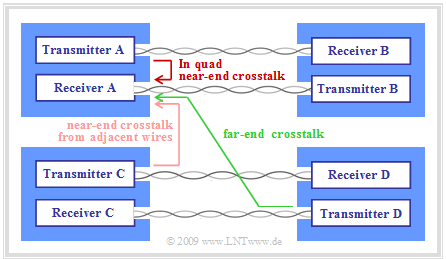
Crosstalk is divided into two types (see graphic):

• Near-end Crosstalk  $\rm (NEXT)$:  The interfering transmitter and the interfered receiver are on the same side of the cable.

• Far-end Crosstalk  $\rm (FEXT)$:  The interfering transmitter and the interfered receiver are on opposite sides of the cable.

Far-end crosstalk decreases sharply with increasing cable length due to attenuation,  so that near-end crosstalk is dominant even with DSL.

$\text{Conclusion:}$  To summarize:

1. As frequency increases and spacing between line pairs decreases  – as within a star quad –  near-end crosstalk increases.  It is less critical if the conductors are in different basic bundles.
   
2. Depending on the stranding technique used,  the shielding and the manufacturing accuracy of the cable,  this effect occurs to varying degrees.  The cable length,  on the other hand,  does not play a role in near-end crosstalk:   The own transmitter is not attenuated by the cable.
   
3. Crosstalk can be significantly reduced by clever assignment,  for example by assigning different services to adjacent pairs,  using different frequency bands with as little overlap as possible.

Signal–to–noise ratio, range and transmission rate

To evaluate the quality of a transmission system,  the signal-to-noise ratio  $\rm (SNR)$  is usually used.  This is also a measure of the expected bit error rate  $\rm (BER)$.

• Signal and noise in the same frequency band reduce the SNR and lead to a higher bit error rate or  – for a given bit error rate –  to a lower transmission bit rate.

• The relationships between transmit power,  channel quality  $($cable attenuation and noise power$)$  and achievable transmission rate can be illustrated very well by Shannon's channel capacity formula:

$$C \left [ \frac{\rm bit}{\rm symbol} \right ] = \frac {1}{2} \cdot \log_2 \left ( 1 + \frac{P_{\rm E}}{P_{\rm N}} \right )= \frac {1}{2} \cdot \log_2 \left ( 1 + \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{P_{\rm N}} \right ) \hspace{0.05cm}.$$

The  »channel capacity«  $C$  denotes the maximum transmission bit rate at which transmission is possible under ideal conditions  $($among others,  the best possible coding with infinite block length$)$   ⇒   »channel coding theorem». For more details,  see the fourth main chapter  "AWGN Channel Capacity for Continuous-Valued Input".

We assume that the bandwidth is fixed by the xDSL variant and that near-end crosstalk is the dominant interference.  Then the transmission rate can be improved by the following measures:

1. For a given transmitted power  $P_{\rm S}$  and a given medium  $($e.g. balanced copper pairs with 0.4 mm diameter$)$,  the received power  $P_{\rm E}$  $($that can be used for demodulation$)$  is increased only by a shorter line length.
2. One reduces the interference power  $P_{\rm N}$,  which for a given bandwidth  $B$  would be achieved by increased crosstalk attenuation,  which in turn also depends on the transmission method on the adjacent line pairs.
3. Increasing the transmitted power  $P_{\rm S}$  would not be effective here,  since a larger transmitted power would at the same time have an unfavorable effect on the crosstalk.  This measure would only be successful for an AWGN channel  $($example:  coaxial cable$)$.

This listing shows that with xDSL there is a direct correlation between

• line length,

• transmission rate,  and

• the transmission method used.

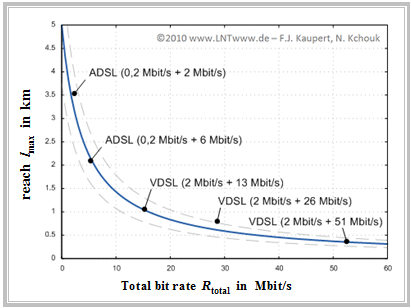
$\text{Example 2:}$  From this graph, which refers to measurements with  "$\rm 1-DA xDSL$"  methods and  $\text{0.4 mm}$  copper cables in test systems with realistic interference conditions,  one can clearly see these dependencies.

Range and total bit rate for ADSL and VDSL

The graph shows for some ADSL and VDSL variants

• the range  $($maximum cable length$)$  $l_{\rm max}$  and

• the total transmission rate  $R_{\rm total}$ 

1. of upstream $($first indication$)$
2. and downstream $($second indication$)$.

The total transmission rate for the systems considered is between  $2.2 \ \rm Mbit/s$  and  $53\ \rm Mbit/s$.

• The trend of the measured values is shown in this graph as a solid  $($blue$)$  curve and can be formulated as a rough approximation as follows:

$$l_{\rm max}\,{\rm \big [in}\,\,{\rm km \big ] } = \frac {20}{4 + R_{\rm total}\,{\rm \big [in}\,\,{\rm Mbit/s \big ] } } \hspace{0.05cm}.$$

• It can be seen that the range of all current systems  $($approximately between half a kilometer and three and a half kilometers of line length$)$  differs from this rule of thumb by a maximum of  $±25\%$  $($dashed curves$)$.

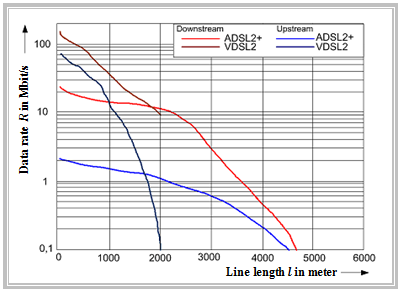
$\text{Example 3:}$  The diagram below shows the total data bit rates of  "ADSL2+"  and  "VDSL(2)"  as a function of line length,

Data bit rates vs. cable lengths for xDSL systems

• with the  $($different$)$  red curves referring to the downstream

• and the two blue curves to the upstream.

This is based on a worst-case interference scenario with the following boundary conditions:

• Cable bundle with  $50$  copper pairs  $(0.4$  mm diameter$)$,  PE insulated,

• target symbol error rate  $p_{\rm S}=10^{-7},\ 6 \ \text{dB}$  margin $($reserve SNR to reach target data rate$)$,

• simultaneous operation of the following transmission methods:

1.     $25$  times  "ADSL2+ over ISDN",
2.     $14$  times ISDN,  four times  "SHDSL"  $(R= \text{1 Mbit/s)}$,
3.     five times each  "SHDS"L  $(R= \text{2 Mbit/s)}$  and  "$(\text{VDSL2 band plan 998}$",
4.     twice  "HDSL".

You can see from this diagram:

• For short line lengths,  the achievable data rates for VDSL(2) are significantly higher than for ADSL2+.

• From a line length of  $\approx 1800$  meters,  ADSL2+ is significantly better than VDSL(2).

• This is due to the fact that VDSL(2) operates in the lower frequency bands with significantly lower power in order to interfere less with neighboring systems.

• As the line length increases,  the higher frequency subchannels become unusable due to increasing attenuation,  which explains the crash in data rate.

Overview of DSL error correction measures

In order to reduce the BER of xDSL systems,  a number of techniques have been cleverly combined in the specifications to counteract the two most common causes of errors:

• Transmission errors due to pulse and crosstalk interference on the line:  
  Especially at high data rates,  adjacent symbols in the QAM signal space are close together,  which significantly increases the bit error probability.

• Cutting off of signal peaks due to lack of dynamic range of the transmitter amplifiers: 
  This  "clipping"  also corresponds to pulse noise and acts as an additional colored noise that noticeably degrades the SNR.

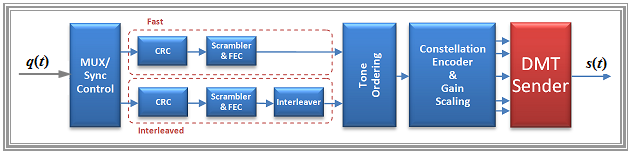
With the DMT method,  two paths are implemented for error correction in the signal processors.  The bit assignment to these paths is done by a multiplexer with sync control.

Complete DSL/DMT system

• In the case of  »fast path«,  low waiting times  $($"latency"$)$  are used.

• With  »interleaved path«,  low bit error rates are in the foreground.  Here the latency is higher due to the use of an interleaver.

• "Dual latency"  means the simultaneous use of both paths.  The  "ADSL Transceiver Units"  must support dual latency at least in the downstream.

The remaining chapter sections discuss error protection procedures for both paths. 

For other modulation methods,  the error protection measures described here are the same in principle,  but different in detail.

1. The transmission chain starts with the  "cyclic redundancy check"  $\rm (CRC)$,  which forms a checksum over an overframe that is evaluated at the receiver.
2. Task of the scrambler is to convert long sequences of  "ones"  and  "zeros"  to produce more frequent signal changes.
3. This is followed by the "forward error correction"  $\rm (FEC)$  to detect/correct byte errors at the receiving end.  Often used for xDSL:  Reed-Solomon and Trellis coding.
4. Task of the  "interleaver"  is to distribute the received code words over a larger time range in order to distribute transmission errors over several code words.
5. After passing through the individual bit protection procedures,  the data streams from fast and interleaved paths are combined and processed in  "tone ordering".
6. In addition,  a guard interval and cyclic prefix are inserted in the DMT transmitter after the IDFT,  which is removed again in the DMT receiver.
7. This represents a very simple realization of signal equalization in the frequency domain when the channel is distorted.

Cyclic redundancy check

The  "cyclic redundancy check"  $\rm (CRC)$  is a simple bit-level procedure to check the integrity of data during transmission or duplication.  The CRC principle has already been described in detail in the  "ISDN chapter".  Here follows a brief summary,  using the nomenclature used in the xDSL specifications:

• For each data block  $D(x)$  with  $k$  bit  $(d_0$, ... , $d_{k-1})$,  a parity-check value  $C(x)$  with eight bits is formed prior to data transmission and appended to the original data sequence  $($the variable  $x$  denotes here the delay operator$)$.

• $C(x)$  is obtained as the division remainder of the modulo-2 polynomial division of  $D(x)$  by the given parity-check polynomial  $G(x)$:

$$D(x) = d_0 \cdot x^{k-1} + d_1 \cdot x^{k-2} + ... + d_{k-2} \cdot x + d_{k-1}\hspace{0.05cm},$$

$$G(x) = x^8 + x^4 + x^3 + x^2 + 1 \hspace{0.05cm},$$

$$C(x) = D(x) \cdot x^8 \,\,{\rm mod }\,\, G(x) = c_0 \cdot x^7 + c_1 \cdot x^6 + \text{...} + c_6 \cdot x + c_7 \hspace{0.05cm}.$$

• Another CRC value is formed at the receiver using the same procedure and compared with the transmitted CRC value.  If both are different,  at least one bit error happened during transmission.

• By this way,  bit errors can be detected if they are not too much clustered.  In ADSL practice,  the CRC procedure is sufficient for bit error detection.

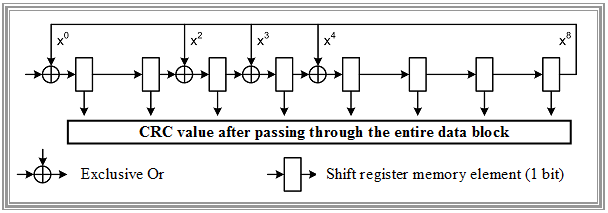
The graph shows an exemplary circuit for the CRC value generation with the generator polynomial  $G(x)$  specified for ADSL – realizable in hardware or software:

Cyclic Redundancy Check for ADSL

1. The data block  $D(x)$  to be tested is introduced into the circuit from the left,  the output is fed back and exclusively-or-linked to the digits of the generator polynomial  $G(x)$.
2. After passing through the entire data block,  the memory elements contain the CRC parity-check value  $C(x)$.
3. It should be noted that with ADSL the data is split into so-called  "superframes"  of 68 frames each.
4. Each frame contains data from the  "fast path"  and the  "interleaved path".  In addition,  management and synchronization bits are transmitted in specific frames.
5. Eight CRC bits are formed per ADSL superframe and per path and are transmitted as  "fast byte"  resp.  "sync byte" as the first byte of frame  "$0$"  of the next superframe.

Scrambler and de–scrambler

Task of the scrambler is to convert long sequences of  "ones"  and  "zeros"  in such a way that frequent symbol changes occur.

• A possible realization is a shift register circuit with feedback exclusive-or-linked branches.

• In order to produce the original binary sequence at the receiver,  a mirror-image self-synchronizing  "de-scrambler"  must be used there.

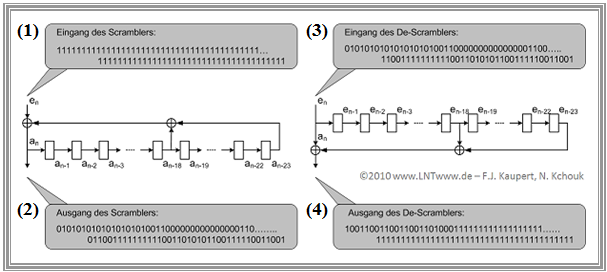
The graph shows on the left an example of a scrambler actually used at DSL with  $23$  memory elements.  The corresponding de-scrambler is shown on the right.

Scrambler and de-scrambler in a DSL/DMT system
    $(1)$   scrambler's input        $(3)$   de-scrambler's input
    $(2)$   scrambler's output     $(4)$   de-scrambler's output

The transmitter-side shift register is loaded with an arbitrary initial value that has no further effect on the operation of the circuit. Here:

$$11001'10011'00110'01100'110.$$

If we denote

• by  $e_n$  the bits of the binary input sequence,  and

• by  $a_n$  the bits at the output, 

the following relation holds:

$$a_n = e_n \oplus a_{n- 18}\oplus a_{n- 23}\hspace{0.05cm}.$$

In the example,  the scrambler input sequence consists of  80  consecutive  "ones"  $($upper left gray background$)$,  which are shifted bit by bit into the scrambler.  The output bit sequence then has frequent  "one-zero"  changes,  as desired.

The de-scrambler  $($shown on the right$)$  can be started at any time with any starting value,  which means that no synchronization is required between the two circuits.  Here:

$$10111'011110'11101'11011'101.$$

The de-scrambler output data stream shows,

• that the de-scrambler initially outputs some  $($up to a maximum of $23)$  erroneous bits,  but then

• synchronizes automatically,  and then

• recovers the original bit sequence  $($only  "ones"$)$  without errors.

Forward error correction

For  "forward error correction"  $\rm (FEC)$,  all xDSL variants use a  "Reed-Solomon-Code".  In some systems  "trellis code modulation"  $\rm (TCM)$  has been made mandatory as an additional error protection measure,  even though it has only been specified as  "optional"  by the international bodies.

Both methods are discussed in detail in the book  "Channel Coding".  Here follows a brief summary of Reed-Solomon coding with respect to its application to DSL:

• With Reed-Solomon encoding,  redundancy bytes are generated for fixed agreed interpolation points of the payload polynomial.  With systematic Reed-Solomon encoding,  a parity-check value is calculated similar to the CRC procedure and appended to the data block to be protected.

• However,  the data is no longer processed  "bit by bit",  but  "byte by byte".  Consequently,  arithmetic operations are no longer performed in the Galois field  $\rm GF( 2 )$  but in  $\rm GF(2^8)$.

The Reed-Solomon parity-check byte can also be determined as the division remainder of a polynomial division,  for xDSL with the following parameters:

1. Number  $S$  of DMT symbols to be monitored per Reed-Solomon code word  $(S \ge 1$  for the fast buffer,  $S =2^0$, ... , $2^4$  for the interleaved buffer$)$,
2. number  $K$  of user data bytes in the  $S$  DMT symbols,  defined as a polynomial  $B(x)$  of degree  $K$,  where the  "B"  indicates  "bytes",
3. Number  $R$  of Reed-Solomon parity-check bytes  $($even number between  $2$  to  $16)$  per parity-check value  $($"fast"  or  "interleaved"$)$,
4. sum  $N = K + R$  of the user data bytes and check bytes of the Reed-Solomon code word.

The specifics of Reed-Solomon encoding for xDSL are given here without further comment:

• For xDSL,  the number  $R$  of check bytes must be an integer multiple of the number  $S$  of symbols so that they can be evenly distributed in the payload polynomial.

• The so-called  "Maximum Distance Separable  $\rm (MDS)$  codes"  – a subclass of Reed-Solomon codes –  allow the correction of  $R/2$  falsified user data bytes.

• From the selected Reed-Solomon code for the DMT systems,  the constraint is a maximum code word length of  $2^8-1 = 255$  bytes corresponding to  $2040$  bits.

• The redundancy of Reed-Solomon codes can generate a considerable amount of data if the parameters are unfavorable,  thus considerably reducing the net data rate.

• It is recommended that the data amount  $($"gross data rate"$)$  be divided judiciously into useful data  $($"net data rate,  payload"$)$  and error protection data  $($"overhead"$)$.

• Reed-Solomon coding achieves a  "high coding gain".  A system without coding would have to have a signal-to-noise ratio  $\rm (SNR)$  larger by  $3 \ \rm dB$  for same bit error rate.

• By  "trellis-encoded modulation"  $\rm (TCM)$  in combination with other error protection measures,  the coding gain is highly variable; it ranges between  $0 \ \rm dB$  and  $6 \ \rm dB$.

Interleaving and de–interleaving

The common task of  "interleaver"  $($at the transmitter$)$  and  "de-interleaver"  $($at the receiver$)$  is

• to spread the received Reed-Solomon code words over a larger time range

• in order to distribute any transmission errors over several code words

• and thus increase the chance of correct decoding.

xDSL interleaving is characterized by the parameter  $D$  $($"depth"$)$,  which can take values between  $2^0$  and  $2^9$ .

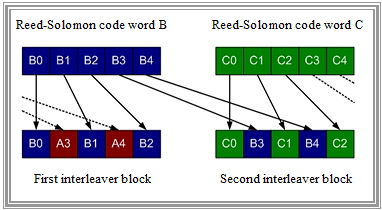
$\text{Example 4:}$  The graph illustrates the principle using the Reed-Solomon code words  $A$,  $B$,  $C$  with five bytes each and the interleaver depth  $D = 2$.

For DSL interleaving with  $D = 2$

Each byte  $B_i$  of the middle Reed-Solomon code word  $B$  is delayed by  $V_i = (D - 1) \cdot i$  bytes. 

Two interleaver blocks are formed:

• The first block contains the bytes  $B_0$,  $B_1$  and  $B_2$  together with the bytes  $A_3$  and  $A_4$  of the previous code word.

• The second block contains the bytes  $B_3$  and  $B_4$  along with the bytes  $C_0$,  $C_1$  and  $C_2$  of the following code word.

This  "scrambling"  has the following advantages  $($provided,  $D$  is sufficiently large$)$:

1. The error correction capabilities of the Reed-Solomon code are improved.
2. The user data rate remains the same,  i.e. is not reduced $($redundancy-free$)$.
3. In the event of errors,  entire packets do not have to be repeated at the protocol level.

A disadvantage is that with increasing interleaver depth  $D$  there can be noticeable delay times  $($on the order of milliseconds$)$,  which causes major problems for real-time applications.  However,  interleaving with low depth is only useful if the signal-to-noise ratio is sufficiently high.

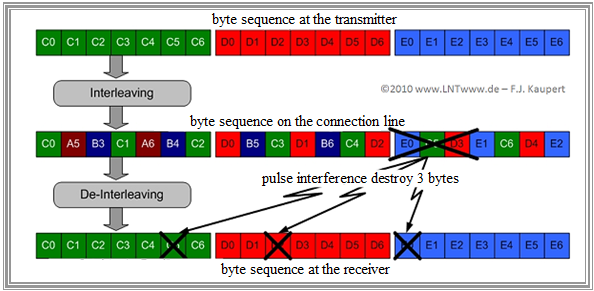
$\text{Example 5:}$  An example of the advantages of interleaver/de-interleaver in the presence of bundle errors is shown in the following graph:

DSL interleaving and de–interleaving with  $D = 3$

• In the first row,  the transmitted byte sequence is shown according to Reed-Solomon encoding,  with each code word consisting of seven bytes as an example.

• In the middle row,  the data bytes are shifted by interleaving with  $D = 3$  so that between  $C_i$  and  $C_{i+1}$  there are two foreign bytes and the green code word is distributed over three blocks.

• Now suppose that during transmission a pulse glitch falsified three consecutive bytes in a single data block.

• After the de-interleaver,  the original byte sequence of the Reed-Solomon code words is restored,  with the three falsified bytes distributed among three independent code words.

• If two redundancy bytes were inserted in each case during the Reed-Solomon encoding,  the now separated byte falsifications can be completely corrected.

Gain scaling and tone ordering

A particularly advantageous feature of DMT is the possibility

1. to adjust the bins individually to the existing channel characteristics and
2. possibly to switch off "bins" with unfavorable SNR completely.

Bit-bin assignment based on SNR

The procedure is as follows:

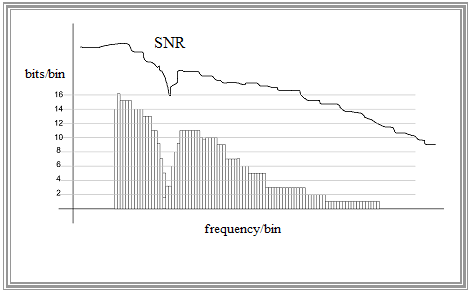
• Before starting the transmission  – and possibly also dynamically during operation –  the DMT modem measures the channel characteristics for each  "bin"  and sets the maximum transmission rate individually according to the SNR  $($see graphic$)$.

• During initialization,  the  "ADSL Transceiver Units"  exchange bin information,  for example the respective  "bits/bin"  and the required transmission power  $($'"gain"$)$.

• Thereby the  $\text{ATU-C}$  sends information about the upstream and the  $\text{ATU-R}$  sends information about the downstream.

• This message is of the format  $\{b_i, g_i\}$  where  $b_i$  $($four bits$)$  indicates the constellation size.  For the upstream,  the index  $i = 1$, ... , $31$  and for the downstream  $i = 1$, ... , $255$.

• The gain  $g_i$  is a fixed-point number with twelve bits.  For example  $g_i = 001.010000000$  represents the decimal value  $1 + 1/4 =1.25$.

• This indicates that the signal power of channel  $i$  must be higher by  $1.94 \ \rm dB$  than the power of the test signal transmitted during the channel analysis.

When operating the fast path and the interleaved path simultaneously $($see  "graphic"  in the section  "DSL error correction measures"$)$,  the bit error rate can be further reduced by optimized carrier frequency allocation  $($"Tone Ordering"$)$.  The background of this measure is again  "clipping"  $($truncation of voltage peaks$)$,  which worsens the overall SNR. This procedure is based on the following rules:

• Bins with dense constellation  $($many bits/bin   ⇒   larger clipping probability$)$  are assigned to the interleaved branch,  since this is per se more reliable due to the additional interleaver.  Accordingly,  the subchannels with low order allocation  $($few bits/bin$)$  are reserved for the fast data buffer.

• New tables are then sent for upstream and downstream,  in which the bins are no longer ordered by index,  but according to the bits/bin ratios.  Based on this new table,  it is possible for the  $\text{ATU-C}$  or  $\text{ATU-R}$  to perform bit extraction successfully.

Inserting guard interval and cyclic prefix

In the chapter  "Realization of OFDM systems"  of the book "Modulation Methods" it has already been shown that by inserting a guard interval. The bit error rate can be decisively improved in the presence of linear channel distortion.

We assume that the cable impulse response  $h_{\rm K}(t)$  extends over the time duration  $T_{\rm K}$.  Ideally  $h_{\rm K}(t) = δ(t)$  and accordingly an infinitely short extension:   $T_{\rm K} = 0$. For distorting channel  $(T_{\rm K} > 0 )$  holds:

• By inserting a "guard interval"  of duration  $T_{\rm G}$  "intersymbol interference"  $\rm (ISI)$  between each DSL frame can be avoided as long as  $T_{\rm G}$ ≥ $T_{\rm K}$  holds. However, this measure leads to a rate loss by a factor  $T/(T + T_{\rm G})$  with symbol duration  $T = {1}/{f_0}$.

• But with this,  there is still "inter-carrier interference"  $\rm (ICI)$  between each subcarrier within the same frame,  that is,  the  "DMT individual spectra"  are no longer  $\rm sinc$-shaped and de-orthogonalization occurs.

• By a  "cyclic prefix"  this disturbing effect can also be avoided.  Here one extends the transmission vector  $\mathbf{s}$  forward by the last  $L$  samples  of the IDFT output,  where the minimum value for  $L$  is given by the duration  $T_{\rm K}$  of the cable impulse response.

$\text{Example 6:}$ 

DMT transmission signal with cyclic prefix

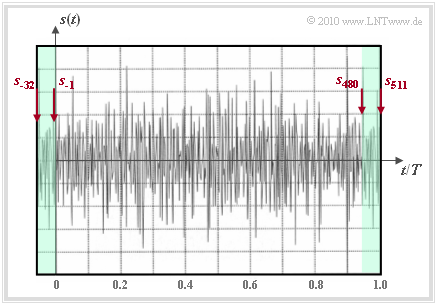
The graphic shows this measure with the DSL/DMT method,  for which the parameter  $L = 32$  has been set:

• The samples  $s_{480}$ , ... , $s_{511}$  are added as prefix  $(s_{-32}$ , ... , $s_{-1})$  to the IDFT output vector  $(s_0$ , ... , $s_{511})$. 

• The transmitted signal  $s(t)$  has now the duration  $T + T_{\rm G} = 1.0625 \cdot T ≈ 246 \ {\rm µ s}$  instead of the symbol duration  $T ≈ 232 \ {\rm µ s}$.  This reduces the rate by a factor of  $0.94$.

• In the receiver-side evaluation, one is restricted to the time range from  $0$  to  $T$. In this time interval the disturbing influence of the impulse response has already decayed and the subchannels are orthogonal to each other - just as with an ideal channel.

• The sample values  $s_{-32}$ , ... , $s_{-1}$  are discarded at the receiver – a rather simple realization of signal equalization.

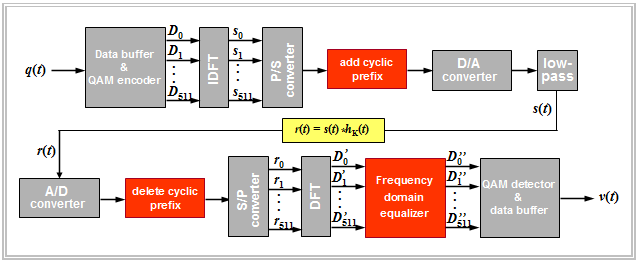
The last diagram in this chapter shows the entire DMT transmission system,  but without the  "error protection measures"  described earlier.  You can see:

DMT–System with cyclic prefix

• In the  "Add cyclic prefix"  block,  the samples  $s_{480}$, ... , $s_{511}$  are added as  $s_{-32}$, ... , $s_{-1}$.  The transmitted signal  $s(t)$  thus has the course shown in  $\text{Example 6}$.

• The received signal  $r(t)$  results from the convolution of  $s(t)$  with the channel impulse response  $h_{\rm K}(t)$.  After A/D conversion and removal of the cyclic prefix,  the input values for the DFT are  $r_0$, ... , $ r_{511}$.

• The  $($complex$)$  output values  $D_k\hspace{0.01cm}'$  of the DFT depend only on the particular  $($complex$)$  data value  $D_k$.  Independently of other data  $D_κ (κ ≠ k)$  holds with the noise value  $n_k\hspace{0.01cm}'$:

$${D}_k\hspace{0.01cm}' = \alpha_k \cdot {D}_k + {n}_k\hspace{0.01cm}', \hspace{0.2cm}\alpha_k = H_{\rm K}( f = f_k) \hspace{0.05cm}. $$

• Each carrier  $D_k$  is modified in amplitude and phase by its own  $($complex$)$  factor  $α_k$,  which depends only on the channel.  The frequency domain equalizer has only the task of multiplying the coefficient  $D_k\hspace{0.01cm}'$  by the inverse value  ${1}/{α_k}$.  Finally,  one obtains:

$$ D''_k = {D}_k + {n}_k \hspace{0.05cm}.$$

$\text{Conclusion:}$ 

• This simple realization possibility of the complete equalization of the strongly distorting cable frequency response was one of the decisive criteria that for  $\rm xDSL$  the  $\rm DMT$ method has prevailed over  $\rm QAM$  and  $\rm CAP$.

• Mostly an additional time-domain pre-equalization takes place directly after the A/D conversion to avoid also intersymbol interference between adjacent frames.

Exercises for the chapter

Exercise 2.5: DSL Error Protection

Exercise 2.5Z: Reach and Bit Rate with ADSL

Exercise 2.6: Cyclic Prefix