Difference between revisions of "Applets:Principle of Pseudo-Ternary Coding"
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEnDe|pseudoternarycodes_en|pseudoternarycodes}} |
| + | |||
| − | == | + | ==Applet Description== |
<br> | <br> | ||
| − | + | The applet covers the properties of the best known pseudo-ternary codes, namely: | |
| − | # | + | # First-order bipolar code, $\rm AMI$ code (from: ''Alternate Mark Inversion''), characterized by the parameters $N_{\rm C} = 1, \ K_{\rm C} = +1$, |
| − | # | + | # Duobinary code, $(\rm DUOB)$, code parameters: $N_{\rm C} = 1, \ K_{\rm C} = -1$, |
| − | # | + | # Second order bipolar code $(\rm BIP2)$, code parameters: $N_{\rm C} = 2, \ K_{\rm C} = +1$. |
| − | + | At the input is the redundancy-free binary bipolar source symbol sequence $\langle \hspace{0.05cm}q_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$ ⇒ rectangular signal $q(t)$ an. Illustrating the generation. | |
| − | * | + | *of the binary–precoded sequence $\langle \hspace{0.05cm}b_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$, represented by the also redundancy-free binary bipolar rectangular signal $b(t)$, |
| − | * | + | *the pseudo-ternary code sequence $\langle \hspace{0.05cm}c_\nu \hspace{0.05cm}\rangle \ \in \{+1,\ 0, -1\}$, represented by the redundant ternary bipolar rectangular signal $c(t)$, |
| − | * | + | *the equally redundant ternary transmitted signal $s(t)$, characterized by the amplitude coefficients $a_\nu $, and the (transmitted–) base impulse $g(t)$: |
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | + | The base impulse $g(t)$ – in the applet "Rectangle", "Nyquist" and "Root–Nyquist" – determines not only the shape of the transmitted signal, but also the course of | |
| − | * | + | * of the auto-correlation function $\rm (ACF)$ $\varphi_s (\tau)$ and |
| − | * | + | * of the associated power spectral density $\rm (PSD)$ ${\it \Phi}_s (f)$. |
| − | + | The applet also shows that the total power spectral density ${\it \Phi}_s (f)$ can be split into the part ${\it \Phi}_a (f)$ that takes into account the statistical relations of the amplitude coefficients $a_\nu$ and the energy spectral density $ {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 $, characterized by the shape $g(t)$. | |
| − | '' | + | ''Note'' In the applet, no distinction is made between the encoder symbols $c_\nu \in \{+1,\ 0, -1\}$ and the amplitude coefficients $a_\nu \in \{+1,\ 0, -1\}$ . It should be remembered that the $a_\nu$ are always numerical values, while for the encoder symbols also the notation $c_\nu \in \{\text{plus},\ \text{zero},\ \text{minus}\}$ would be admissible. |
| − | == | + | ==Theoretical Background== |
| − | == | + | == General description of the pseudo-multilevel codes == |
| + | <br> | ||
| + | In symbolwise coding, each incoming source symbol $q_\nu$ generates an encoder symbol $c_\nu$, which depends not only on the current input symbol $q_\nu$ but also on the $N_{\rm C}$ preceding symbols $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $. $N_{\rm C}$ is referred to as the "order" of the code.<br> | ||
| − | + | Typical for symbolwise coding is that | |
| + | *the symbol duration $T$ of the encoded signal (and of the transmitted signal) matches the bit duration $T_{\rm B}$ of the binary source signal, and | ||
| − | + | *encoding and decoding do not lead to major time delays, which are unavoidable when block codes are used.<br><br> | |
| − | + | The "pseudo-multilevel codes" – better known as "partial response codes" – are of special importance. In the following, only "pseudo-ternary codes" ⇒ level number $M = 3$ are considered. | |
| − | + | *These can be described by the block diagram corresponding to the left graph. | |
| − | * | + | *In the right graph an equivalent circuit is given, which is very suitable for an analysis of these codes. |
| − | + | [[File:EN_Dig_T_2_4_S1_v23.png|right|frame|Block diagram (above) and equivalent circuit (below) of a pseudo-ternary encoder|class=fit]] | |
| − | |||
| − | |||
| − | |||
| − | + | One can see from the two representations: | |
| − | * | + | *The pseudo-ternary encoder can be split into the "non-linear pre-encoder" and the "linear coding network", if the delay by $N_{\rm C} \cdot T$ and the weighting by $K_{\rm C}$ are drawn twice for clarity – as shown in the right equivalent figure. |
| − | * | + | *The "non-linear pre-encoder" obtains the precoded symbols $b_\nu$, which are also binary, by a modulo–2 addition ("antivalence") between the symbols $q_\nu$ and $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $: |
:$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | :$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | ||
+1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | ||
+1\}\hspace{0.05cm}.$$ | +1\}\hspace{0.05cm}.$$ | ||
| − | * | + | *Like the source symbols $q_\nu$, the symbols $b_\nu$ are statistically independent of each other. Thus, the pre-encoder does not add any redundancy. However, it allows a simpler realization of the decoder and prevents error propagation after a transmission error.<br> |
| − | * | + | *The actual encoding from binary $(M_q = 2)$ to ternary $(M = M_c = 3)$ is done by the "linear coding network" by the conventional subtraction |
:$$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm | :$$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm | ||
C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | ||
| − | : | + | :which can be described by the following [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|"impulse response"]] resp. [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain#Frequency_response_.E2.80.93_Transfer_function|"transfer function"]] with respect to the input signal $b(t)$ and the output signal $c(t)$: |
:$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | :$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | ||
C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | ||
| − | * | + | *The relative redundancy is the same for all pseudo-ternary codes. Substituting $M_q=2$, $M_c=3$ and $T_c =T_q$ into the [[Digital_Signal_Transmission/Redundancy-Free_Coding#Symbolwise_coding_vs._blockwise_coding|"general definition equation"]], we obtain |
:$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$ | :$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | + | The $\text{transmitted signal of all pseudo-ternary codes}$ is always represented as follows: | |
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | * | + | *The property of the current pseudo-ternary code is reflected in the statistical bonds between the $a_\nu$ In all cases $a_\nu \in \{-1, \ 0, +1\}$. |
| − | * | + | *The basic transmitting pulse $g(t)$ provides on the one hand the required energy, but has also influence on the statistical bonds within the signal. |
| − | * | + | *In addition to the NRZ rectangular pulse $g_{\rm R}(t)$ can be selected in the program: |
| − | :* | + | :*the Nyquist impulse ⇒ impulse response of the raised cosine low-pass with rolloff factor $r$: |
:$$g_{\rm Nyq}(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T) \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\rm Nyq}(f),$$ | :$$g_{\rm Nyq}(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T) \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\rm Nyq}(f),$$ | ||
| − | :* | + | :*the root Nyquist impulse ⇒ impulse response of the root raised cosine low-pass with rolloff factor $r$: |
:$$g_{\sqrt{\rm Nyq} }(t)\ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\sqrt{\rm Nyq} }(f)={\rm const.} \cdot \sqrt{G_{\rm Nyq}(f)} .$$ }} | :$$g_{\sqrt{\rm Nyq} }(t)\ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\sqrt{\rm Nyq} }(f)={\rm const.} \cdot \sqrt{G_{\rm Nyq}(f)} .$$ }} | ||
<br><br> | <br><br> | ||
| − | === | + | == Properties of the AMI code== |
| + | <br> | ||
| + | The individual pseudo-ternary codes differ in the $N_{\rm C}$ and $K_{\rm C}$ parameters. The best-known representative is the '''first-order bipolar code''' with the code parameters | ||
| + | :* $N_{\rm C} = 1$, | ||
| + | :* $K_{\rm C} = 1$, | ||
| − | |||
| − | + | which is also known as '''AMI code''' (from: "Alternate Mark Inversion"). This is used e.g. with [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_ISDN|"ISDN"]] ("Integrated Services Digital Networks") on the so-called $S_0$ interface. | |
| − | |||
| − | + | [[File:EN_Dig_T_2_4_S2a.png|right|frame|Signals with AMI coding and HDB3 coding|class=fit]] | |
| − | * | + | *The graph above shows the binary source signal $q(t)$. |
| − | + | ||
| + | *The second and third diagrams show: | ||
| + | :* the likewise binary signal $b(t)$ after the pre-encoder, and | ||
| + | :* the encoded signal $c(t) = s(t)$ of the AMI code. | ||
| − | |||
| − | |||
| − | |||
| − | + | One can see the simple AMI encoding principle: | |
| + | #Each binary value "–1" of the source signal $q(t)$ ⇒ symbol $\rm L$ is encoded by the ternary amplitude coefficient $a_\nu = 0$. <br><br> | ||
| + | #The binary value "+1" of the source signal $q(t)$ ⇒ symbol $\rm H$ is alternately represented by $a_\nu = +1$ and $a_\nu = -1$. <br><br> | ||
| − | + | This ensures that the AMI encoded signal does not contain any "long sequences"<br> | |
| + | * $ \langle c_\nu \rangle = \langle \text{...}, +1, +1, +1, +1, +1, \text{...}\rangle$ resp. | ||
| + | * $ \langle c_\nu \rangle = \langle \text{...}, -1, -1, -1, -1, -1, \text{...}\rangle$, | ||
| − | |||
| − | |||
| − | + | which would lead to problems with a DC-free channel. | |
| − | * | + | On the other hand, the occurrence of long zero sequences is quite possible, where no clock information is transmitted over a longer period of time. |
| − | * | + | <br clear = all> |
| + | To avoid this second problem, some modified AMI codes have been developed, for example the "B6ZS code" and the "HDB3 code": | ||
| + | *In the '''HDB3 code''' (green curve in the graphic), four consecutive zeros in the AMI encoded signal are replaced by a subsequence that violates the AMI encoding rule.<br> | ||
| + | |||
| + | *In the gray shaded area, this is the sequence "$+\ 0\ 0\ +$", since the last symbol before the replacement was a "minus".<br> | ||
| + | |||
| + | *This limits the number of consecutive zeros to $3$ for the HDB3 code and to $5$ for the [https://www.itwissen.info/en/bipolar-with-six-zero-substitution-B6ZS-121675.html#gsc.tab=0 "B6ZS code"]. | ||
| + | |||
| + | *The decoder detects this code violation and replaces "$+\ 0\ 0\ +$" with "$0\ 0\ 0\ 0$" again.<br> | ||
<br><br> | <br><br> | ||
| − | === | + | === Calculating the ACF of a digital signal === |
| − | In | + | In the execution of the experiment some quantities and correlations are used, which shall be briefly explained here: |
| − | * | + | * The (time-unlimited) digital signal includes both the source statistics $($amplitude coefficients $a_\nu$) and the transmitted pulse shape $g(t)$: |
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g ( t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g ( t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | * | + | * If $s(t)$ is the pattern function of a stationary and ergodic random process, then for the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Random_processes|"Auto-Correlation Function"]] $\rm (ACF)$: |
:$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | :$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | ||
\cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | ||
\lambda \cdot T)\hspace{0.05cm}.$$ | \lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | * | + | * This equation describes the convolution of the discrete ACF $\varphi_a(\lambda) = {\rm E}\big [ a_\nu \cdot a_{\nu + \lambda}\big]$ of the amplitude coefficients with the energy–ACF of the base impulse: |
:$$\varphi^{^{\bullet} }_{g}(\tau) = | :$$\varphi^{^{\bullet} }_{g}(\tau) = | ||
| Line 120: | Line 133: | ||
\tau)\,{\rm d} t \hspace{0.05cm}.$$ | \tau)\,{\rm d} t \hspace{0.05cm}.$$ | ||
| − | * | + | *The point is to indicate that $\varphi^{^{\bullet} }_{g}(\tau)$ has the unit of an energy, while $\varphi_s(\tau)$ indicates a power and $\varphi_a(\lambda)$ is dimensionless. |
<br> | <br> | ||
| − | === | + | === Calculating the PSD of a digital signal === |
| − | + | The corresponding quantity to the ACF in the frequency domain is the [[Theory_of_Stochastic_Signals/Power-Spectral_Density#Wiener-Khintchine_Theorem|"Power Spectral Density"]] $\rm (PSD)$ ${\it \Phi}_s(f)$, which is fixedly related to $\varphi_s(\tau)$ via the Fourier integral:<br> | |
:$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | :$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | ||
{\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | ||
{\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} | {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} | ||
\,{\rm d} \tau \hspace{0.05cm}.$$ | \,{\rm d} \tau \hspace{0.05cm}.$$ | ||
| − | * | + | *The power spectral density ${\it \Phi}_s(f)$ can be represented as a product of two functions, taking into account the dimensional adjustment $(1/T)$ : |
:$${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot | :$${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot | ||
|G_s(f)|^2 \hspace{0.05cm}.$$ | |G_s(f)|^2 \hspace{0.05cm}.$$ | ||
| − | * | + | *The first term ${\it \Phi}_a(f)$ is dimensionless and describes the spectral shaping of the transmitted signal by the statistical relations of the source:<br> |
:$$\varphi_a(\lambda) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}{\it \Phi}_a(f) = \sum_{\lambda = | :$$\varphi_a(\lambda) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}{\it \Phi}_a(f) = \sum_{\lambda = | ||
-\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm | -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm | ||
| Line 138: | Line 151: | ||
1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f | 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f | ||
\lambda T) \hspace{0.05cm}.$$ | \lambda T) \hspace{0.05cm}.$$ | ||
| − | *${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$ | + | *${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$ takes into account the spectral shaping by $g(t)$. The narrower this is, the wider $\vert G(f) \vert^2$ and thus the larger the bandwidth requirement: |
:$$\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | :$$\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | ||
{\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 | {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The energy spectral density ${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$ has the unit $\rm Ws/Hz$ and the power spectral density ${\it \Phi_{s}}(f)$ after division by the symbol spacing $T$ has the unit $\rm W/Hz$. |
| Line 148: | Line 161: | ||
| − | + | == Power-spectral density of the AMI code== | |
| − | + | <br> | |
| − | + | The frequency response of the linear code network of a pseudo-ternary code is generally: | |
:$$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm | :$$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm | ||
e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} | e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} | ||
| Line 160: | Line 173: | ||
\big ]\hspace{0.05cm}.$$ | \big ]\hspace{0.05cm}.$$ | ||
| − | + | This gives the power-spectral density $\rm (PSD)$ of the amplitude coefficients $(K$ and $\alpha$ are abbreviations according to the above equation$)$: | |
:$$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos | :$$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos | ||
(\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos | (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos | ||
(\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos | (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos | ||
(\alpha) \big ] $$ | (\alpha) \big ] $$ | ||
| − | [[File:P_ID1347__Dig_T_2_4_S2b_v2.png|right|frame| | + | [[File:P_ID1347__Dig_T_2_4_S2b_v2.png|right|frame|Power-spectral density of the AMI code|class=fit]] |
:$$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos | :$$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos | ||
(2\pi f N_{\rm C} T)\big ] | (2\pi f N_{\rm C} T)\big ] | ||
| Line 171: | Line 184: | ||
\varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$ | \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | + | In particular, for the power-spectral density of the AMI code $(N_{\rm C} = K_{\rm C} = 1)$, we obtain: | |
:$${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos | :$${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos | ||
(2\pi f T)\big ] = \sin^2 | (2\pi f T)\big ] = \sin^2 | ||
(\pi f T)\hspace{0.05cm}.$$ | (\pi f T)\hspace{0.05cm}.$$ | ||
| − | + | The graph shows | |
| − | * | + | *the PSD ${\it \Phi}_a(f)$ of the amplitude coefficients (red curve), and<br> |
| − | * | + | |
| + | *the PSD ${\it \Phi}_s(f)$ of the total transmitted signal (blue), valid for NRZ rectangular pulses.<br> | ||
| − | + | One recognizes from this representation | |
| − | * | + | *that the AMI code has no DC component, since ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$, <br> |
| − | |||
| + | *the power $P_{\rm S} = s_0^2/2$ of the AMI-coded transmitted signal $($integral over ${\it \Phi}_s(f)$ from $- \infty$ to $+\infty)$. | ||
| − | |||
| − | |||
| − | |||
| + | Notes: | ||
| + | *The PSD of the HDB3 and B6ZS codes differs only slightly from that of the AMI code.<br> | ||
| − | + | *You can use the (German language) SWF applet [[Applets:Pseudoternaercodierung|"Signals, ACF, and PSD of pseudo-ternary codes"]] to clarify the topic discussed here. | |
| − | + | ||
| − | + | == Properties of the duobinary code == | |
| + | <br> | ||
| + | The '''duobinary code''' is defined by the code parameters $N_{\rm C} = 1$ and $K_{\rm C} = -1$. This gives the power-spectral density $\rm (PSD)$ of the amplitude coefficients and the PSD of the transmitted signal: | ||
| + | [[File:P_ID1348__Dig_T_2_4_S3b_v1.png|right|frame|Power-spectral density of the duobinary code|right|class=fit]] | ||
:$${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos | :$${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos | ||
| Line 204: | Line 220: | ||
(2 \pi f T) \hspace{0.05cm}.$$ | (2 \pi f T) \hspace{0.05cm}.$$ | ||
| − | + | The graph shows the power-spectral density | |
| − | * | + | *of the amplitude coefficients ⇒ ${\it \Phi}_a(f)$ as a red curve,<br> |
| − | |||
| − | In | + | *of the total transmitted signal ⇒ ${\it \Phi}_s(f)$ as a blue curve.<br><br> |
| − | [[File:P_ID1349__Dig_T_2_4_S3a_v2.png|left|frame| | + | |
| − | <br><br> | + | In the second graph, the signals $q(t)$, $b(t)$ and $c(t) = s(t)$ are sketched. We refer here again to the (German language) SWF applet [[Applets:Pseudoternaercodierung|"Signals, ACF, and PSD of pseudo-ternary codes"]], which also clarifies the duobinary code. |
| − | * | + | |
| − | + | [[File:P_ID1349__Dig_T_2_4_S3a_v2.png|left|frame|Signals in duobinary coding|class=fit]] | |
| − | * | + | <br><br><br><br><br><br>From these illustrations it is clear: |
| − | + | *In the duobinary code, any number of symbols with same polarity ("+1" or "–1") can directly succeed each other ⇒ ${\it \Phi}_a(f = 0)=1$, ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.<br> | |
| − | * | + | |
| + | *In contrast, for the duobinary code, the alternating sequence "... , +1, –1, +1, –1, +1, ..." does not occur, which is particularly disturbing with respect to intersymbol interference. Therefore, in the duobinary code: ${\it \Phi}_s(f = 1/(2T) = 0$.<br> | ||
| + | |||
| + | *The power-spectral density ${\it \Phi}_s(f)$ of the pseudo-ternary duobinary code is identical to the PSD with redundancy-free binary coding at half rate $($symbol duration $2T)$.<br> | ||
<br clear= all> | <br clear= all> | ||
| − | == | + | ==Exercises== |
| − | |||
<br> | <br> | ||
| − | * | + | *First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number "$0$" corresponds to a "Reset": Same setting as at program start. |
| − | + | *A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution". | |
| − | + | ||
| − | |||
| − | |||
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(1)''' | + | '''(1)''' Consider and interpret the binary pre–coding of the $\text{AMI}$ code using the source symbol sequence $\rm C$ assuming $b_0 = +1$. }} |
| − | * | + | *The modulo–2 addition can also be taken as "antivalence". It holds $b_{\nu} = +1$, if $q_{\nu}$ and $b_{\nu - 1}$ differ, otherwise set $b_{\nu} = -1$ : |
: $b_1 = (q_1 = +1)\ {\rm XOR}\ (b_0= +1) = -1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (b_1= -1) = -1,\ \ b_3 = (q_3 = -1)\ {\rm XOR}\ (b_2= -1) = -1,$ | : $b_1 = (q_1 = +1)\ {\rm XOR}\ (b_0= +1) = -1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (b_1= -1) = -1,\ \ b_3 = (q_3 = -1)\ {\rm XOR}\ (b_2= -1) = -1,$ | ||
: $b_4 = (q_4 = +1)\ {\rm XOR}\ (b_3= -1) = +1,\ \ b_5 = (q_5 = +1)\ {\rm XOR}\ (b_4= +1) = -1,\ \ b_6 = (q_6 = +1)\ {\rm XOR}\ (b_5= -1) = +1,\ \ b_7 = b_8 = \text{...} = -1.$ | : $b_4 = (q_4 = +1)\ {\rm XOR}\ (b_3= -1) = +1,\ \ b_5 = (q_5 = +1)\ {\rm XOR}\ (b_4= +1) = -1,\ \ b_6 = (q_6 = +1)\ {\rm XOR}\ (b_5= -1) = +1,\ \ b_7 = b_8 = \text{...} = -1.$ | ||
| − | * | + | *With the initial condition $b_0 = -1$ we get the negated sequence: $b_4 = b_6 =-1$. All others $b_\nu = +1$. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(2)''' | + | '''(2)''' Let $b_0 = +1$. Consider the AMI encoded sequence $\langle c_\nu \rangle$ of the source symbol sequence $\rm C$ and give their amplitude coefficients $a_\nu$. }} |
| − | * | + | *It holds: $a_1= 0.5 \cdot (b_1-b_0) = -1$, $a_2= 0.5 \cdot (b_2-b_1) =0$, $a_3= 0. 5 \cdot (b_3-b_2) =0$, $a_4= +1$, $a_5= -1$, $a_6= +1$, $a_7= -1$, $a_8= a_9 = \text{...} = 0$. |
| − | * | + | *In contrast to the pre–coding, the conventional addition (subtraction) is to be applied here and not the modulo–2 addition. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(3)''' | + | '''(3)''' Now consider the AMI coding for several random sequences. What rules can be derived from these experiments for the amplitude coefficients $a_\nu$ ?}} |
| − | * | + | *Each binary value "–1" of $q(t)$ ⇒ symbol $\rm L$ is encoded by the ternary coefficient $a_\nu = 0$. Any number of $a_\nu = 0$ can be consecutive. |
| − | * | + | *The binary value "+1" of $q(t)$ ⇒ symbol $\rm H$ is represented alternatively with $a_\nu = +1$ and $a_\nu = -1$ , starting with $a_\nu = -1$, if $b_0 = +1$. |
| − | * | + | *From the source symbol sequence $\rm A$ ⇒ $\langle \hspace{0.05cm}q_\nu \equiv +1 \hspace{0.05cm}\rangle$ the code symbol sequence $+1, -1, +1, -1, \text{...}$ . Long sequences $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$ or $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$ are shot out. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(4)''' | + | '''(4)''' Continue with AMI coding. Interpret the autocorrelation function $\varphi_a(\lambda)$ of the amplitude coefficients and the power density spectrum ${\it \Phi}_a(f)$. }} |
| − | * | + | *The discrete ACF $\varphi_a(\lambda)$ of the amplitude coefficients is only defined for integer $\lambda$ values. With AMI coding $(N_{\rm C}=1)$ holds: For $|\lambda| > 1$ ⇒ all $\varphi_a(\lambda)= 0$. |
| − | *$\varphi_a(\lambda = 0)$ | + | *$\varphi_a(\lambda = 0)$ is equal to the root mean square of the amplitude coefficients ⇒ $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$ |
| − | * | + | *Only the combinations $(+1, -1)$ and $(-1, +1)$ contribute to the expected value ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$ Result: $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$ |
| − | * | + | *The power density spectrum ${\it \Phi}_a(f)$ is the Fourier transform of the discrete ACF $\varphi_a(\lambda)$. Result: ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 |
| − | (\pi | + | (\pi f T)\hspace{0.05cm}.$ |
| − | * | + | *From ${\it \Phi}_a(f = 0) = 0$ follows: The AMI code is especially interesting for channels over which no DC component can be transmitted. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(5)''' | + | '''(5)''' We consider further AMI coding and rectangular pulses. Interpret the ACF $\varphi_s(\tau)$ of the transmission signal and the PDS ${\it \Phi}_s(f)$. }} |
| − | *$\varphi_s(\tau)$ | + | *$\varphi_s(\tau)$ results from the convolution of the discrete AKF $\varphi_a(\lambda)$ with $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$. For rectangular pulses $($duration $T)$: The energy–AKF $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$ is a triangle of duration $2T$. |
| − | * | + | *It holds $\varphi_s(\tau = 0)= \varphi_a(\lambda = 0) =0.5, \ \varphi_s(\pm T)= \varphi_a( 1) =-0. 25,\ , \ \varphi_s( \pm 2T)= \varphi_a(2) =0.$ Between these discrete values, $\varphi_{s}(\tau)$ is always linear. |
| − | * | + | *The PDS ${\it \Phi}_s(f)$ is obtained from ${\it \Phi}_a(f) = \sin^2(\pi f T)$ by multiplying with ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = {\rm sinc}^2(f T).$ This does not change anything at the zeros of ${\it \Phi}_a(f)$ . |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(6)''' | + | '''(6)''' What changes with respect to $s(t)$, $\varphi_s(\tau)$ and ${\it \Phi}_s(f)$ with the $\rm Nyquist$ pulse? Vary the roll–off factor here in the range $0 \le r \le 1$.}} |
| − | * | + | *A single Nyquist pulse can be represented with the source symbol sequence $\rm B$ in the $s(t)$ range. You can see equidistant zero crossings in the distance $T$. |
| − | * | + | *Also, for any AMI random sequence, the signal values $s(t=\nu \cdot T)$ for each $r$ correspond exactly to their nominal positions. Outside these points, there are deviations. |
| − | * | + | *In the special case $r=0$ the energy–LDS ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ is constant in the range $|f|<1/2T$. Accordingly, the energy–ACF ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ has a $\rm sinc$ shape. |
| − | * | + | *On the other hand, for larger $r$ the zeros of ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ are no longer equidistant, since although $G(f)$ satisfies the first Nyquist criterion, it does not ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$. |
| − | * | + | *The main advantage of the Nyquist pulse is the much smaller bandwidth. Here only the frequency range $|f| < (1+r)/(2T)$ has to be provided. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(7)''' | + | '''(7)''' Repeat the last experiment using the $\text{Root raised cosine}$ pulse instead of the Nyquist pulse. Interpret the results. }} |
| − | * | + | *In the special case $r=0$ the results are as in '''(6)'''. ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ is constant in the range $|f|<1/2T$ and outside zero; ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ has a $\rm sinc$ shape. |
| − | * | + | *Also for larger $r$ the zeros of ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ are eqidistant (but not $\rm sinc$ shaped) ⇒ ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$ satisfies the first Nyquist criterion. |
| − | * | + | *On the other hand, $G(f)$ does not satisfy the first Nyquist criterion $($except for $r=0)$. Intersymbol interference occurs already at the transmitter ⇒ signal $s(t)$. |
| − | * | + | *But this is also not a fundamental problem. By using an identically shaped reception filter like $G(f)$ intersymbol interference at the decider is avoided. |
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''(8)''' | + | '''(8)''' Consider and check the pre–coding $(b_\nu)$ and the amplitude coefficients $(a_\nu)$ with the $\rm duobinary$ coding $($source symbol sequence $\rm C$, $b_0 = +1)$. }} |
*$b_1 = (q_1 = +1)\ {\rm XOR}\ (\overline{b_0}= -1) = +1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (\overline{b_1}= -1) = -1,\ \ b_3 = \text{...} =b_7 = +1,$ $b_8 = b_{10} = \text{...} =-1$, $b_9 =b_{11} = \text{...}= +1$. | *$b_1 = (q_1 = +1)\ {\rm XOR}\ (\overline{b_0}= -1) = +1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (\overline{b_1}= -1) = -1,\ \ b_3 = \text{...} =b_7 = +1,$ $b_8 = b_{10} = \text{...} =-1$, $b_9 =b_{11} = \text{...}= +1$. | ||
| − | *$a_1= 0.5 \cdot (b_1+b_0) = +1$, $a_2= 0.5 \cdot (b_2+b_1) =0$, $a_3= 0.5 \cdot (b_3+b_2) = 0$, $a_4= | + | *$a_1= 0.5 \cdot (b_1+b_0) = +1$, $a_2= 0.5 \cdot (b_2+b_1) =0$, $a_3= 0.5 \cdot (b_3+b_2) = 0$, $a_4= \text{...}= a_7=+1$, $a_8=a_9= \text{...}= 0$. |
| − | * | + | *With the starting condition $b_0 = -1$ we get again the negated sequence: $a_1= -1$, $a_2= a_3= 0$, $a_4= \text{...}= a_7=-1$, $a_8=a_9= \text{...}= 0$. |
| + | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(9)''' Now consider the Duobinary coding for several random sequences. What rules can be derived from these experiments for the amplitude coefficients $a_\nu$?}} | ||
| − | {{ | + | *The discrete ACF values are $\varphi_a(\lambda = 0) = +0.5$, $\varphi_a(\lambda = 1) = +0.25$, $\varphi_a(\lambda = 2) = 0$ ⇒ ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 |
| − | + | (\pi f T)\hspace{0.05cm}.$ | |
| + | *Unlike the AMI coding, the encoded sequences $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$ and $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$ are possible here ⇒ For the Duobinary code holds ${\it \Phi}_a(f= 0) = 1 \ (\ne 0).$ | ||
| + | *As with the AMI code, the "long zero sequence" ⇒ $\langle \hspace{0.05cm}a_\nu \equiv 0 \hspace{0.05cm}\rangle$ is possible, which can again lead to synchronization problems. | ||
| + | *Excluded are the combinations $a_\nu = +1, \ a_{\nu+1} = -1$ and $a_\nu = -1, \ a_{\nu+1} = +1$, recognizable by the PDS value ${\it \Phi}_a(f= 1/(2T)) = 0.$ | ||
| + | *Such direct transitions $a_\nu = +1$ ⇒ $a_{\nu+1} = -1$ resp. $a_\nu = -1$ ⇒ $a_{\nu+1} = +1$ lead to large intersymbol interference and thus to a higher error rate. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(10)''' Compare the coding results of second order bipolar code $\rm (BIP2)$ and first order bipolar code $\rm (AMI)$ for different source symbol sequences. }} | ||
| + | *For a single rectangular pulse ⇒ source symbol sequence $\rm B$ both codes result in the same encoded sequence and the same encoded signal $c(t)$ ⇒ also an isolated pulse. | ||
| + | *The "Permanent–One sequence" $\rm A$ now results $\langle c_\nu \rangle = \langle -1, -1, +1, +1, -1, -1, +1, +1, \text{. ..}\rangle $ instead of $\langle c_\nu \rangle = \langle -1, +1, -1, +1, -1, +1, \text{...}\rangle $. | ||
| + | *The simple decoding algorithm of the AMI code $($the ternary $0$ becomes the binary $-1$, the ternary $\pm 1$ becomes the binary $+1)$ cannot be applied to $\rm BIP2$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(11)''' View and interpret the various ACF and LDS graphs of the $\rm BIP2$ compared to the $\rm AMI$ code.}} | ||
| + | *For $\rm AMI$: $\varphi_a(\lambda = \pm 1) = -0.25, \ \varphi_a(\lambda = \pm 2) = 0$. For $\rm BIP2$: $\varphi_a(\lambda = \pm 1) = 0, \ \varphi_a(\lambda = \pm 2) = -0.25$. In both cases: $\varphi_a(\lambda = 0) = 0.5$. | ||
| + | *From the $\rm AMI$ power density spectrum ${\it \Phi}_a(f) = \sin^2 (\pi \cdot f T)$ follows for $\rm BIP2$: ${\it \Phi}_a(f) = \sin^2 (2\pi \cdot f T)$ by compression with respect to the $f$–axis. | ||
| + | *Zero at $f=0$: At most two $+1$ directly follow each other, and also at most only two $-1$. In the AMI code $+1$ and $-1$ occur only in isolation. | ||
| + | *Next zero at $f=1/(2T)$: The infinitely long $(+1, -1)$ sequence is excluded in $\rm BIP2$ as in the $\rm Duobinary$ code. | ||
| + | *Consider and interpret also the functions $\varphi_s(\tau)$ and ${\it \Phi}_s(f)$ for the pulses "rectangle", "Nyquist" and "Root raised cosine". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Applet Manual== |
| − | [[File:BS_Pseudoternär.png|right|600px|frame| | + | [[File:BS_Pseudoternär.png|right|600px|frame|Screenshot (German version, light background)]] |
<br> | <br> | ||
| − | '''(A)''' Theme ( | + | '''(A)''' Theme (changeable graphical user interface design) |
| − | :* Dark: | + | :* Dark: dark background (recommended by the authors) |
| − | :* Bright: | + | :* Bright: white background (recommended for beamers and printouts) |
| − | :* Deuteranopia: | + | :* Deuteranopia: for users with pronounced green visual impairment |
| − | :* Protanopia: | + | :* Protanopia: for users with pronounced red visual impairment |
| − | '''(B)''' | + | '''(B)''' Underlying block diagram |
| − | '''(C)''' | + | '''(C)''' Selection of the pseudoternary code: |
| − | <br> | + | <br> AMI–code, duobinary code, 2nd order bipolar code. |
| − | '''(D)''' | + | '''(D)''' Selection of the base pulse $g(t)$: |
| − | <br> | + | <br> Rectangular pulse, Nyquist pulse, Root–Nyquist pulse. |
| − | '''(E)''' Rolloff– | + | '''(E)''' Rolloff–factor (frequency range) for "Nyquist" and "Root–Nyquist" |
| − | '''(F)''' | + | '''(F)''' Setting of $3 \cdot 4 = 12$ Bit of source symbol sequence. |
| − | '''(G)''' | + | '''(G)'''' Selection of one of three preset source symbol sequences. |
| − | '''(H)''' | + | '''(H)''' Random binary source symbol sequence. |
| − | '''( I )''' | + | '''( I )''' Stepwise elucidation of pseudoternary coding. |
| − | '''(J)''' | + | '''(J)''' Result of pseudoternary coding: Signals $q(t)$, $b(t)$, $c(t)$, $s(t)$ |
| − | '''(K)''' | + | '''(K)''' Deleting the signal waveforms in the graphics area $\rm M$ |
| − | '''(L)''' | + | '''(L)''' Sketches for autocorrelation function & power spectral density. |
| − | '''(M)''' | + | '''(M)''' Graphics area: Source signal $q(t)$, signal $b(t)$ after precoding, <br> encoder signal $c(t)$ with rectangles, transmission signal $s(t)$ according to $g(t)$ |
| − | '''(N)''' | + | '''(N)''' Area for exercises: Exercise selection, questions, sample solution. |
<br clear=all> | <br clear=all> | ||
| − | == | + | ==About the Authors== |
| − | + | This interactive calculation tool was designed and implemented at the [https://www.ei.tum.de/en/lnt/home/ Institute for Communications Engineering] at the [https://www.tum.de/en Technical University of Munich]. | |
| − | * | + | *The first version was created in 2010 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Stefan_M.C3.BCller_.28Diplomarbeit_LB_2010.29|Stefan Müller]] as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | * 2020 | + | *In 2020 the program was redesigned by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] as part of her bachelor thesis (Supervisor: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ) via "HTML5". |
| − | + | *Last revision and English version 2021 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] in the context of a working student activity. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | The conversion of this applet to HTML 5 was financially supported by [https://www.ei.tum.de/studium/studienzuschuesse/ "Studienzuschüsse"] (Faculty EI of the TU Munich). We thank. | ||
| + | <br><br> | ||
| − | == | + | ==Once again: Open Applet in new Tab== |
| − | {{ | + | {{LntAppletLinkEnDe|pseudoternarycodes_en|pseudoternarycodes}} |
Latest revision as of 18:26, 14 April 2023
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
The applet covers the properties of the best known pseudo-ternary codes, namely:
- First-order bipolar code, $\rm AMI$ code (from: Alternate Mark Inversion), characterized by the parameters $N_{\rm C} = 1, \ K_{\rm C} = +1$,
- Duobinary code, $(\rm DUOB)$, code parameters: $N_{\rm C} = 1, \ K_{\rm C} = -1$,
- Second order bipolar code $(\rm BIP2)$, code parameters: $N_{\rm C} = 2, \ K_{\rm C} = +1$.
At the input is the redundancy-free binary bipolar source symbol sequence $\langle \hspace{0.05cm}q_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$ ⇒ rectangular signal $q(t)$ an. Illustrating the generation.
- of the binary–precoded sequence $\langle \hspace{0.05cm}b_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$, represented by the also redundancy-free binary bipolar rectangular signal $b(t)$,
- the pseudo-ternary code sequence $\langle \hspace{0.05cm}c_\nu \hspace{0.05cm}\rangle \ \in \{+1,\ 0, -1\}$, represented by the redundant ternary bipolar rectangular signal $c(t)$,
- the equally redundant ternary transmitted signal $s(t)$, characterized by the amplitude coefficients $a_\nu $, and the (transmitted–) base impulse $g(t)$:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$
The base impulse $g(t)$ – in the applet "Rectangle", "Nyquist" and "Root–Nyquist" – determines not only the shape of the transmitted signal, but also the course of
- of the auto-correlation function $\rm (ACF)$ $\varphi_s (\tau)$ and
- of the associated power spectral density $\rm (PSD)$ ${\it \Phi}_s (f)$.
The applet also shows that the total power spectral density ${\it \Phi}_s (f)$ can be split into the part ${\it \Phi}_a (f)$ that takes into account the statistical relations of the amplitude coefficients $a_\nu$ and the energy spectral density $ {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 $, characterized by the shape $g(t)$.
Note In the applet, no distinction is made between the encoder symbols $c_\nu \in \{+1,\ 0, -1\}$ and the amplitude coefficients $a_\nu \in \{+1,\ 0, -1\}$ . It should be remembered that the $a_\nu$ are always numerical values, while for the encoder symbols also the notation $c_\nu \in \{\text{plus},\ \text{zero},\ \text{minus}\}$ would be admissible.
Theoretical Background
General description of the pseudo-multilevel codes
In symbolwise coding, each incoming source symbol $q_\nu$ generates an encoder symbol $c_\nu$, which depends not only on the current input symbol $q_\nu$ but also on the $N_{\rm C}$ preceding symbols $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $. $N_{\rm C}$ is referred to as the "order" of the code.
Typical for symbolwise coding is that
- the symbol duration $T$ of the encoded signal (and of the transmitted signal) matches the bit duration $T_{\rm B}$ of the binary source signal, and
- encoding and decoding do not lead to major time delays, which are unavoidable when block codes are used.
The "pseudo-multilevel codes" – better known as "partial response codes" – are of special importance. In the following, only "pseudo-ternary codes" ⇒ level number $M = 3$ are considered.
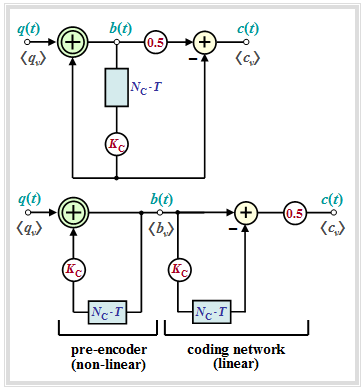
- These can be described by the block diagram corresponding to the left graph.
- In the right graph an equivalent circuit is given, which is very suitable for an analysis of these codes.
One can see from the two representations:
- The pseudo-ternary encoder can be split into the "non-linear pre-encoder" and the "linear coding network", if the delay by $N_{\rm C} \cdot T$ and the weighting by $K_{\rm C}$ are drawn twice for clarity – as shown in the right equivalent figure.
- The "non-linear pre-encoder" obtains the precoded symbols $b_\nu$, which are also binary, by a modulo–2 addition ("antivalence") between the symbols $q_\nu$ and $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $:
- $$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.$$
- Like the source symbols $q_\nu$, the symbols $b_\nu$ are statistically independent of each other. Thus, the pre-encoder does not add any redundancy. However, it allows a simpler realization of the decoder and prevents error propagation after a transmission error.
- The actual encoding from binary $(M_q = 2)$ to ternary $(M = M_c = 3)$ is done by the "linear coding network" by the conventional subtraction
- $$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$
- which can be described by the following "impulse response" resp. "transfer function" with respect to the input signal $b(t)$ and the output signal $c(t)$:
- $$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$
- The relative redundancy is the same for all pseudo-ternary codes. Substituting $M_q=2$, $M_c=3$ and $T_c =T_q$ into the "general definition equation", we obtain
- $$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$
The $\text{transmitted signal of all pseudo-ternary codes}$ is always represented as follows:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$
- The property of the current pseudo-ternary code is reflected in the statistical bonds between the $a_\nu$ In all cases $a_\nu \in \{-1, \ 0, +1\}$.
- The basic transmitting pulse $g(t)$ provides on the one hand the required energy, but has also influence on the statistical bonds within the signal.
- In addition to the NRZ rectangular pulse $g_{\rm R}(t)$ can be selected in the program:
- the Nyquist impulse ⇒ impulse response of the raised cosine low-pass with rolloff factor $r$:
- $$g_{\rm Nyq}(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T) \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\rm Nyq}(f),$$
- the root Nyquist impulse ⇒ impulse response of the root raised cosine low-pass with rolloff factor $r$:
- $$g_{\sqrt{\rm Nyq} }(t)\ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\sqrt{\rm Nyq} }(f)={\rm const.} \cdot \sqrt{G_{\rm Nyq}(f)} .$$
Properties of the AMI code
The individual pseudo-ternary codes differ in the $N_{\rm C}$ and $K_{\rm C}$ parameters. The best-known representative is the first-order bipolar code with the code parameters
- $N_{\rm C} = 1$,
- $K_{\rm C} = 1$,
which is also known as AMI code (from: "Alternate Mark Inversion"). This is used e.g. with "ISDN" ("Integrated Services Digital Networks") on the so-called $S_0$ interface.
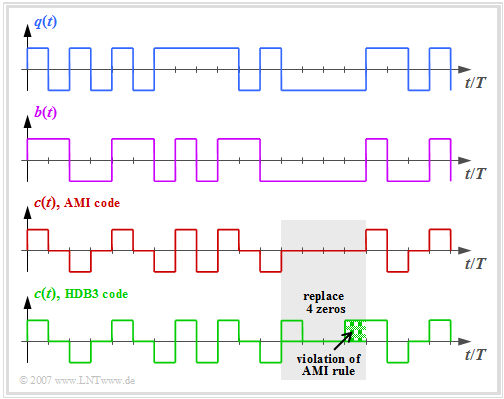
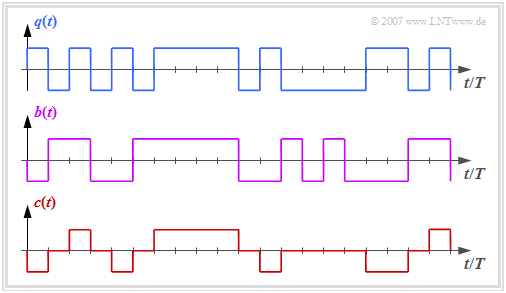
- The graph above shows the binary source signal $q(t)$.
- The second and third diagrams show:
- the likewise binary signal $b(t)$ after the pre-encoder, and
- the encoded signal $c(t) = s(t)$ of the AMI code.
One can see the simple AMI encoding principle:
- Each binary value "–1" of the source signal $q(t)$ ⇒ symbol $\rm L$ is encoded by the ternary amplitude coefficient $a_\nu = 0$.
- The binary value "+1" of the source signal $q(t)$ ⇒ symbol $\rm H$ is alternately represented by $a_\nu = +1$ and $a_\nu = -1$.
This ensures that the AMI encoded signal does not contain any "long sequences"
- $ \langle c_\nu \rangle = \langle \text{...}, +1, +1, +1, +1, +1, \text{...}\rangle$ resp.
- $ \langle c_\nu \rangle = \langle \text{...}, -1, -1, -1, -1, -1, \text{...}\rangle$,
which would lead to problems with a DC-free channel.
On the other hand, the occurrence of long zero sequences is quite possible, where no clock information is transmitted over a longer period of time.
To avoid this second problem, some modified AMI codes have been developed, for example the "B6ZS code" and the "HDB3 code":
- In the HDB3 code (green curve in the graphic), four consecutive zeros in the AMI encoded signal are replaced by a subsequence that violates the AMI encoding rule.
- In the gray shaded area, this is the sequence "$+\ 0\ 0\ +$", since the last symbol before the replacement was a "minus".
- This limits the number of consecutive zeros to $3$ for the HDB3 code and to $5$ for the "B6ZS code".
- The decoder detects this code violation and replaces "$+\ 0\ 0\ +$" with "$0\ 0\ 0\ 0$" again.
Calculating the ACF of a digital signal
In the execution of the experiment some quantities and correlations are used, which shall be briefly explained here:
- The (time-unlimited) digital signal includes both the source statistics $($amplitude coefficients $a_\nu$) and the transmitted pulse shape $g(t)$:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g ( t - \nu \cdot T)\hspace{0.05cm}.$$
- If $s(t)$ is the pattern function of a stationary and ergodic random process, then for the "Auto-Correlation Function" $\rm (ACF)$:
- $$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
- This equation describes the convolution of the discrete ACF $\varphi_a(\lambda) = {\rm E}\big [ a_\nu \cdot a_{\nu + \lambda}\big]$ of the amplitude coefficients with the energy–ACF of the base impulse:
- $$\varphi^{^{\bullet} }_{g}(\tau) = \int_{-\infty}^{+\infty} g ( t ) \cdot g ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$$
- The point is to indicate that $\varphi^{^{\bullet} }_{g}(\tau)$ has the unit of an energy, while $\varphi_s(\tau)$ indicates a power and $\varphi_a(\lambda)$ is dimensionless.
Calculating the PSD of a digital signal
The corresponding quantity to the ACF in the frequency domain is the "Power Spectral Density" $\rm (PSD)$ ${\it \Phi}_s(f)$, which is fixedly related to $\varphi_s(\tau)$ via the Fourier integral:
- $$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$$
- The power spectral density ${\it \Phi}_s(f)$ can be represented as a product of two functions, taking into account the dimensional adjustment $(1/T)$ :
- $${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$$
- The first term ${\it \Phi}_a(f)$ is dimensionless and describes the spectral shaping of the transmitted signal by the statistical relations of the source:
- $$\varphi_a(\lambda) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}{\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm}.$$
- ${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$ takes into account the spectral shaping by $g(t)$. The narrower this is, the wider $\vert G(f) \vert^2$ and thus the larger the bandwidth requirement:
- $$\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 \hspace{0.05cm}.$$
- The energy spectral density ${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$ has the unit $\rm Ws/Hz$ and the power spectral density ${\it \Phi_{s}}(f)$ after division by the symbol spacing $T$ has the unit $\rm W/Hz$.
Power-spectral density of the AMI code
The frequency response of the linear code network of a pseudo-ternary code is generally:
- $$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi\hspace{0.03cm}\cdot \hspace{0.03cm}f \hspace{0.03cm}\cdot \hspace{0.03cm} N_{\rm C}\hspace{0.03cm}\cdot \hspace{0.03cm}T} \big] ={1}/{2} \cdot \big [1 - K \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} \alpha} \big ]\hspace{0.05cm}.$$
This gives the power-spectral density $\rm (PSD)$ of the amplitude coefficients $(K$ and $\alpha$ are abbreviations according to the above equation$)$:
- $$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos (\alpha) \big ] $$
- $$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ] \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$
In particular, for the power-spectral density of the AMI code $(N_{\rm C} = K_{\rm C} = 1)$, we obtain:
- $${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$$
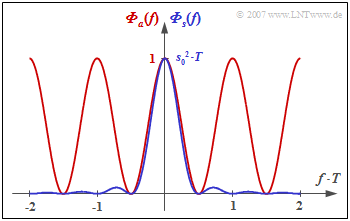
The graph shows
- the PSD ${\it \Phi}_a(f)$ of the amplitude coefficients (red curve), and
- the PSD ${\it \Phi}_s(f)$ of the total transmitted signal (blue), valid for NRZ rectangular pulses.
One recognizes from this representation
- that the AMI code has no DC component, since ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$,
- the power $P_{\rm S} = s_0^2/2$ of the AMI-coded transmitted signal $($integral over ${\it \Phi}_s(f)$ from $- \infty$ to $+\infty)$.
Notes:
- The PSD of the HDB3 and B6ZS codes differs only slightly from that of the AMI code.
- You can use the (German language) SWF applet "Signals, ACF, and PSD of pseudo-ternary codes" to clarify the topic discussed here.
Properties of the duobinary code
The duobinary code is defined by the code parameters $N_{\rm C} = 1$ and $K_{\rm C} = -1$. This gives the power-spectral density $\rm (PSD)$ of the amplitude coefficients and the PSD of the transmitted signal:
- $${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm},$$
- $$ {\it \Phi}_s(f) = s_0^2 \cdot T \cdot \cos^2 (\pi f T)\cdot {\rm si}^2 (\pi f T)= s_0^2 \cdot T \cdot {\rm si}^2 (2 \pi f T) \hspace{0.05cm}.$$
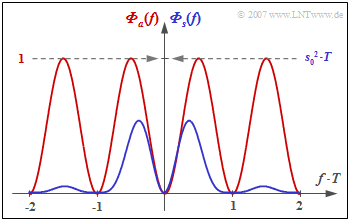
The graph shows the power-spectral density
- of the amplitude coefficients ⇒ ${\it \Phi}_a(f)$ as a red curve,
- of the total transmitted signal ⇒ ${\it \Phi}_s(f)$ as a blue curve.
In the second graph, the signals $q(t)$, $b(t)$ and $c(t) = s(t)$ are sketched. We refer here again to the (German language) SWF applet "Signals, ACF, and PSD of pseudo-ternary codes", which also clarifies the duobinary code.
From these illustrations it is clear:
- In the duobinary code, any number of symbols with same polarity ("+1" or "–1") can directly succeed each other ⇒ ${\it \Phi}_a(f = 0)=1$, ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.
- In contrast, for the duobinary code, the alternating sequence "... , +1, –1, +1, –1, +1, ..." does not occur, which is particularly disturbing with respect to intersymbol interference. Therefore, in the duobinary code: ${\it \Phi}_s(f = 1/(2T) = 0$.
- The power-spectral density ${\it \Phi}_s(f)$ of the pseudo-ternary duobinary code is identical to the PSD with redundancy-free binary coding at half rate $($symbol duration $2T)$.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number "$0$" corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
(1) Consider and interpret the binary pre–coding of the $\text{AMI}$ code using the source symbol sequence $\rm C$ assuming $b_0 = +1$.
- The modulo–2 addition can also be taken as "antivalence". It holds $b_{\nu} = +1$, if $q_{\nu}$ and $b_{\nu - 1}$ differ, otherwise set $b_{\nu} = -1$ :
- $b_1 = (q_1 = +1)\ {\rm XOR}\ (b_0= +1) = -1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (b_1= -1) = -1,\ \ b_3 = (q_3 = -1)\ {\rm XOR}\ (b_2= -1) = -1,$
- $b_4 = (q_4 = +1)\ {\rm XOR}\ (b_3= -1) = +1,\ \ b_5 = (q_5 = +1)\ {\rm XOR}\ (b_4= +1) = -1,\ \ b_6 = (q_6 = +1)\ {\rm XOR}\ (b_5= -1) = +1,\ \ b_7 = b_8 = \text{...} = -1.$
- With the initial condition $b_0 = -1$ we get the negated sequence: $b_4 = b_6 =-1$. All others $b_\nu = +1$.
(2) Let $b_0 = +1$. Consider the AMI encoded sequence $\langle c_\nu \rangle$ of the source symbol sequence $\rm C$ and give their amplitude coefficients $a_\nu$.
- It holds: $a_1= 0.5 \cdot (b_1-b_0) = -1$, $a_2= 0.5 \cdot (b_2-b_1) =0$, $a_3= 0. 5 \cdot (b_3-b_2) =0$, $a_4= +1$, $a_5= -1$, $a_6= +1$, $a_7= -1$, $a_8= a_9 = \text{...} = 0$.
- In contrast to the pre–coding, the conventional addition (subtraction) is to be applied here and not the modulo–2 addition.
(3) Now consider the AMI coding for several random sequences. What rules can be derived from these experiments for the amplitude coefficients $a_\nu$ ?
- Each binary value "–1" of $q(t)$ ⇒ symbol $\rm L$ is encoded by the ternary coefficient $a_\nu = 0$. Any number of $a_\nu = 0$ can be consecutive.
- The binary value "+1" of $q(t)$ ⇒ symbol $\rm H$ is represented alternatively with $a_\nu = +1$ and $a_\nu = -1$ , starting with $a_\nu = -1$, if $b_0 = +1$.
- From the source symbol sequence $\rm A$ ⇒ $\langle \hspace{0.05cm}q_\nu \equiv +1 \hspace{0.05cm}\rangle$ the code symbol sequence $+1, -1, +1, -1, \text{...}$ . Long sequences $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$ or $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$ are shot out.
(4) Continue with AMI coding. Interpret the autocorrelation function $\varphi_a(\lambda)$ of the amplitude coefficients and the power density spectrum ${\it \Phi}_a(f)$.
- The discrete ACF $\varphi_a(\lambda)$ of the amplitude coefficients is only defined for integer $\lambda$ values. With AMI coding $(N_{\rm C}=1)$ holds: For $|\lambda| > 1$ ⇒ all $\varphi_a(\lambda)= 0$.
- $\varphi_a(\lambda = 0)$ is equal to the root mean square of the amplitude coefficients ⇒ $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$
- Only the combinations $(+1, -1)$ and $(-1, +1)$ contribute to the expected value ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$ Result: $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$
- The power density spectrum ${\it \Phi}_a(f)$ is the Fourier transform of the discrete ACF $\varphi_a(\lambda)$. Result: ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$
- From ${\it \Phi}_a(f = 0) = 0$ follows: The AMI code is especially interesting for channels over which no DC component can be transmitted.
(5) We consider further AMI coding and rectangular pulses. Interpret the ACF $\varphi_s(\tau)$ of the transmission signal and the PDS ${\it \Phi}_s(f)$.
- $\varphi_s(\tau)$ results from the convolution of the discrete AKF $\varphi_a(\lambda)$ with $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$. For rectangular pulses $($duration $T)$: The energy–AKF $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$ is a triangle of duration $2T$.
- It holds $\varphi_s(\tau = 0)= \varphi_a(\lambda = 0) =0.5, \ \varphi_s(\pm T)= \varphi_a( 1) =-0. 25,\ , \ \varphi_s( \pm 2T)= \varphi_a(2) =0.$ Between these discrete values, $\varphi_{s}(\tau)$ is always linear.
- The PDS ${\it \Phi}_s(f)$ is obtained from ${\it \Phi}_a(f) = \sin^2(\pi f T)$ by multiplying with ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = {\rm sinc}^2(f T).$ This does not change anything at the zeros of ${\it \Phi}_a(f)$ .
(6) What changes with respect to $s(t)$, $\varphi_s(\tau)$ and ${\it \Phi}_s(f)$ with the $\rm Nyquist$ pulse? Vary the roll–off factor here in the range $0 \le r \le 1$.
- A single Nyquist pulse can be represented with the source symbol sequence $\rm B$ in the $s(t)$ range. You can see equidistant zero crossings in the distance $T$.
- Also, for any AMI random sequence, the signal values $s(t=\nu \cdot T)$ for each $r$ correspond exactly to their nominal positions. Outside these points, there are deviations.
- In the special case $r=0$ the energy–LDS ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ is constant in the range $|f|<1/2T$. Accordingly, the energy–ACF ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ has a $\rm sinc$ shape.
- On the other hand, for larger $r$ the zeros of ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ are no longer equidistant, since although $G(f)$ satisfies the first Nyquist criterion, it does not ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$.
- The main advantage of the Nyquist pulse is the much smaller bandwidth. Here only the frequency range $|f| < (1+r)/(2T)$ has to be provided.
(7) Repeat the last experiment using the $\text{Root raised cosine}$ pulse instead of the Nyquist pulse. Interpret the results.
- In the special case $r=0$ the results are as in (6). ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ is constant in the range $|f|<1/2T$ and outside zero; ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ has a $\rm sinc$ shape.
- Also for larger $r$ the zeros of ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ are eqidistant (but not $\rm sinc$ shaped) ⇒ ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$ satisfies the first Nyquist criterion.
- On the other hand, $G(f)$ does not satisfy the first Nyquist criterion $($except for $r=0)$. Intersymbol interference occurs already at the transmitter ⇒ signal $s(t)$.
- But this is also not a fundamental problem. By using an identically shaped reception filter like $G(f)$ intersymbol interference at the decider is avoided.
(8) Consider and check the pre–coding $(b_\nu)$ and the amplitude coefficients $(a_\nu)$ with the $\rm duobinary$ coding $($source symbol sequence $\rm C$, $b_0 = +1)$.
- $b_1 = (q_1 = +1)\ {\rm XOR}\ (\overline{b_0}= -1) = +1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (\overline{b_1}= -1) = -1,\ \ b_3 = \text{...} =b_7 = +1,$ $b_8 = b_{10} = \text{...} =-1$, $b_9 =b_{11} = \text{...}= +1$.
- $a_1= 0.5 \cdot (b_1+b_0) = +1$, $a_2= 0.5 \cdot (b_2+b_1) =0$, $a_3= 0.5 \cdot (b_3+b_2) = 0$, $a_4= \text{...}= a_7=+1$, $a_8=a_9= \text{...}= 0$.
- With the starting condition $b_0 = -1$ we get again the negated sequence: $a_1= -1$, $a_2= a_3= 0$, $a_4= \text{...}= a_7=-1$, $a_8=a_9= \text{...}= 0$.
(9) Now consider the Duobinary coding for several random sequences. What rules can be derived from these experiments for the amplitude coefficients $a_\nu$?
- The discrete ACF values are $\varphi_a(\lambda = 0) = +0.5$, $\varphi_a(\lambda = 1) = +0.25$, $\varphi_a(\lambda = 2) = 0$ ⇒ ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm}.$
- Unlike the AMI coding, the encoded sequences $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$ and $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$ are possible here ⇒ For the Duobinary code holds ${\it \Phi}_a(f= 0) = 1 \ (\ne 0).$
- As with the AMI code, the "long zero sequence" ⇒ $\langle \hspace{0.05cm}a_\nu \equiv 0 \hspace{0.05cm}\rangle$ is possible, which can again lead to synchronization problems.
- Excluded are the combinations $a_\nu = +1, \ a_{\nu+1} = -1$ and $a_\nu = -1, \ a_{\nu+1} = +1$, recognizable by the PDS value ${\it \Phi}_a(f= 1/(2T)) = 0.$
- Such direct transitions $a_\nu = +1$ ⇒ $a_{\nu+1} = -1$ resp. $a_\nu = -1$ ⇒ $a_{\nu+1} = +1$ lead to large intersymbol interference and thus to a higher error rate.
(10) Compare the coding results of second order bipolar code $\rm (BIP2)$ and first order bipolar code $\rm (AMI)$ for different source symbol sequences.
- For a single rectangular pulse ⇒ source symbol sequence $\rm B$ both codes result in the same encoded sequence and the same encoded signal $c(t)$ ⇒ also an isolated pulse.
- The "Permanent–One sequence" $\rm A$ now results $\langle c_\nu \rangle = \langle -1, -1, +1, +1, -1, -1, +1, +1, \text{. ..}\rangle $ instead of $\langle c_\nu \rangle = \langle -1, +1, -1, +1, -1, +1, \text{...}\rangle $.
- The simple decoding algorithm of the AMI code $($the ternary $0$ becomes the binary $-1$, the ternary $\pm 1$ becomes the binary $+1)$ cannot be applied to $\rm BIP2$ .
(11) View and interpret the various ACF and LDS graphs of the $\rm BIP2$ compared to the $\rm AMI$ code.
- For $\rm AMI$: $\varphi_a(\lambda = \pm 1) = -0.25, \ \varphi_a(\lambda = \pm 2) = 0$. For $\rm BIP2$: $\varphi_a(\lambda = \pm 1) = 0, \ \varphi_a(\lambda = \pm 2) = -0.25$. In both cases: $\varphi_a(\lambda = 0) = 0.5$.
- From the $\rm AMI$ power density spectrum ${\it \Phi}_a(f) = \sin^2 (\pi \cdot f T)$ follows for $\rm BIP2$: ${\it \Phi}_a(f) = \sin^2 (2\pi \cdot f T)$ by compression with respect to the $f$–axis.
- Zero at $f=0$: At most two $+1$ directly follow each other, and also at most only two $-1$. In the AMI code $+1$ and $-1$ occur only in isolation.
- Next zero at $f=1/(2T)$: The infinitely long $(+1, -1)$ sequence is excluded in $\rm BIP2$ as in the $\rm Duobinary$ code.
- Consider and interpret also the functions $\varphi_s(\tau)$ and ${\it \Phi}_s(f)$ for the pulses "rectangle", "Nyquist" and "Root raised cosine".
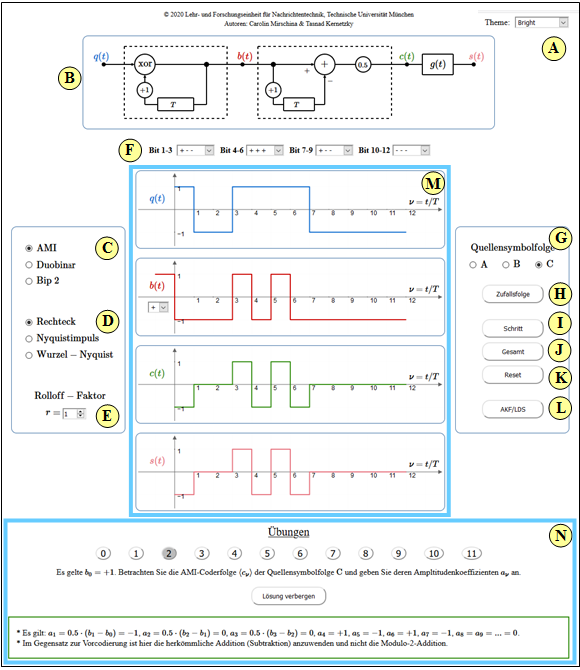
Applet Manual
(A) Theme (changeable graphical user interface design)
- Dark: dark background (recommended by the authors)
- Bright: white background (recommended for beamers and printouts)
- Deuteranopia: for users with pronounced green visual impairment
- Protanopia: for users with pronounced red visual impairment
(B) Underlying block diagram
(C) Selection of the pseudoternary code:
AMI–code, duobinary code, 2nd order bipolar code.
(D) Selection of the base pulse $g(t)$:
Rectangular pulse, Nyquist pulse, Root–Nyquist pulse.
(E) Rolloff–factor (frequency range) for "Nyquist" and "Root–Nyquist"
(F) Setting of $3 \cdot 4 = 12$ Bit of source symbol sequence.
(G)' Selection of one of three preset source symbol sequences.
(H) Random binary source symbol sequence.
( I ) Stepwise elucidation of pseudoternary coding.
(J) Result of pseudoternary coding: Signals $q(t)$, $b(t)$, $c(t)$, $s(t)$
(K) Deleting the signal waveforms in the graphics area $\rm M$
(L) Sketches for autocorrelation function & power spectral density.
(M) Graphics area: Source signal $q(t)$, signal $b(t)$ after precoding,
encoder signal $c(t)$ with rectangles, transmission signal $s(t)$ according to $g(t)$
(N) Area for exercises: Exercise selection, questions, sample solution.
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2010 by Stefan Müller as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- In 2020 the program was redesigned by Carolin Mirschina as part of her bachelor thesis (Supervisor: Tasnád Kernetzky ) via "HTML5".
- Last revision and English version 2021 by Carolin Mirschina in the context of a working student activity.
The conversion of this applet to HTML 5 was financially supported by "Studienzuschüsse" (Faculty EI of the TU Munich). We thank.