Difference between revisions of "Signal Representation/Fourier Series"
| (39 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Periodic Signals |
|Vorherige Seite=Harmonic Oscillation | |Vorherige Seite=Harmonic Oscillation | ||
| − | |Nächste Seite=Fourier Transform and | + | |Nächste Seite=The Fourier Transform and its Inverse |
}} | }} | ||
| − | ==General | + | ==General description== |
<br> | <br> | ||
| − | Every periodic function $x(t)$ can be | + | Every periodic function $x(t)$ can be developed into a trigonometric series called »Fourier series« in all areas, where it is continuous or has only finite discontinuities. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | The '''Fourier series''' of a periodic signal $x(t)$ is defined as follows | + | The »'''Fourier series'''« of a periodic signal $x(t)$ is defined as follows: |
:$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$ | :$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$ | ||
Here the symbols denote the following definitions: | Here the symbols denote the following definitions: | ||
| − | *$A_0$ the '''constant component'''& | + | *$A_0$ the »'''constant component'''« of $x(t)$, |
| − | |||
| − | |||
| − | |||
| + | *$A_n$ the »'''cosine coefficients'''« with $n \ge 1$, | ||
| − | + | *$B_n$ the »'''sine coefficients'''« with $n \ge 1$, | |
| − | *If the Fourier series is interrupted and only $N$ of $A_n$ and $B_n$ coefficients | + | *$\omega_0 = 2\pi/T_0$ the »'''basic circular frequency'''« of the periodic signal $(T_0$ is the period duration$)$.}} |
| + | |||
| + | |||
| + | If the Fourier series should exactly match the actual periodic signal $x(t)$, an infinite number of cosine and sine coefficients must generally be used for calculation. | ||
| + | |||
| + | *If the Fourier series is interrupted and only $N$ of $A_n$ and $B_n$ coefficients are used, then a slightly different plot of the function results except for some special cases: | ||
:$$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$ | :$$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$ | ||
| Line 39: | Line 42: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 1:}$ | $\text{Example 1:}$ | ||
| − | We consider two periodic square | + | We consider two periodic rectangular signals $($"square waves"$)$, each with period duration $T_0$ and basic circular frequency $\omega_0 = 2\pi/T_0$. |
| − | [[File:P_ID525__Sig_T_2_4_S1_neu.png|right|frame|Even and | + | [[File:P_ID525__Sig_T_2_4_S1_neu.png|right|frame|Even and odd rectangular signal]] |
| − | *For the even time signal sketched above: $x_{\rm g}(-t) = x_{\rm g}(t)$ | + | *For the even $($German: "gerade" ⇒ $\rm g)$ time signal sketched above: |
| − | *The function shown below is odd: $x_{\rm u}(-t) = -x_{\rm u}(t)$ | + | :$$x_{\rm g}(-t) = x_{\rm g}(t).$$ |
| − | + | *The function shown below is odd $($German: "ungerade" ⇒ $\rm u)$: | |
| + | :$$x_{\rm u}(-t) = -x_{\rm u}(t).$$ | ||
| − | One finds the | + | One finds the Fourier series representations of both signals in formularies: |
:$$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$ | :$$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$ | ||
| Line 53: | Line 57: | ||
*Because of the generally valid relationship | *Because of the generally valid relationship | ||
| − | :$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4}$$ | + | :$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4},$$ |
| − | the amplitudes (maximum values) of the | + | :the amplitudes $($maximum values$)$ of the rectangular basic pulse result to $1$. |
| − | *This can also be verified using the signal curves in the | + | |
| + | *This can also be verified using the signal curves in the graphic: | ||
:$$x_{\rm g}(t = 0) = x_{\rm u}(t = T_0/4) = 1.$$}} | :$$x_{\rm g}(t = 0) = x_{\rm u}(t = T_0/4) = 1.$$}} | ||
| − | ==Calculation of the Fourier | + | ==Calculation of the Fourier coefficients== |
<br> | <br> | ||
| − | The Fourier coefficient $A_0$ specifies the | + | The Fourier coefficient $A_0$ specifies the »direct current $\rm (DC)$ signal component« which can be determined by averaging over the signal course $x(t)$. Due to the periodicity, averaging over one period is sufficient: |
:$$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$ | :$$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$ | ||
| − | The integration limits can also be selected from $t = 0$ to $t = T_0$ (or over a differently defined period of equal length). | + | *The integration limits can also be selected from $t = 0$ to $t = T_0$ $($or over a differently defined period of equal length$)$. |
| − | The determination of the Fourier coefficients $A_n$ and $B_n$ $(n \ge 1)$ is based on the property that | + | *The determination of the Fourier coefficients $A_n$ and $B_n$ $(n \ge 1)$ is based on the property that cosine and sine functions are so-called [https://en.wikipedia.org/wiki/Orthogonal_functions »orthogonal functions«]. |
| + | |||
| + | *For them the following applies: | ||
| − | :$$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \ | + | :$$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \hspace{0.2cm} m=n,\atop \rm otherwise} \right.$$ |
| − | :$$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \ | + | :$$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \hspace{0.2cm} m=n,\atop \rm otherwise} \right.$$ |
| − | :$$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \ | + | :$$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \hspace{1.2cm} \rm for\ all \hspace{0.2cm} \it m, \ n.$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ Considering these equations, the cosine coefficients $A_n$ and the sine coefficients $B_n$ result as follows | + | $\text{Conclusion:}$ Considering these equations, the cosine coefficients $A_n$ and the sine coefficients $B_n$ result as follows |
:$$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$ | :$$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$ | ||
| Line 85: | Line 92: | ||
| − | The | + | The following $($German-language$)$ learning video illustrates these equations:<br> [[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|»Zur Berechnung der Fourierkoeffizienten«]] ⇒ "Calculating the Fourier coefficients". |
| + | |||
| + | |||
| + | [[File:P_ID526__Sig_T_2_4_S2_neu.png|right|frame|On calculating the Fourier coefficients]] | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 2:}$ | $\text{Example 2:}$ | ||
| Line 94: | Line 103: | ||
:$$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$ | :$$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$ | ||
| − | Since the integral of the cosine and sine functions | + | *Since the integral of the cosine and sine functions over one period are identical to zero, the DC signal coefficient is |
| + | :$$A_0 = 0.4.$$ | ||
| − | One determines the cosine coefficient $A_1$ with | + | *One determines the cosine coefficient $A_1$ with following equation $($Integration limits from $t = 0$ to $t = T_0)$: |
:$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | :$$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$ | ||
| − | The last integral is equal to zero due to orthogonality; the first one is zero too (integral over one period). | + | #The last integral is equal to zero due to orthogonality; the first one is zero too $($integral over one period$)$. |
| − | + | #Only the middle term contributes here to $A_1$, namely $2 - 0.6 - 0.5 = 0.6. $ | |
| − | |||
| + | *For all further $(n \ge 2)$ cosine coefficients all three integrals return the value zero, and thus $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$. | ||
| − | To determine the sine coefficients $B_n$ | + | *To determine the sine coefficients $B_n$ using following equation: |
:$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | :$$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$ | ||
| − | + | #For $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ all three integral values are zero and therefore $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$ | |
| − | + | #On the other hand, for $n=3$ the last integral provides a contribution, and one gets for the sine coefficient | |
| + | ::$$B_3 = -0.3.$$}} | ||
| − | ==Exploitation of | + | ==Exploitation of symmetries== |
<br> | <br> | ||
| − | Some insights into the Fourier coefficients $A_n$ and $B_n$ can already be read from the | + | Some insights into the Fourier coefficients $A_n$ and $B_n$ can already be read from the »symmetry properties« of the time function $x(t)$. |
| − | *If the time signal $x(t)$ is an even function ⇒ axis-symmetrical around the ordinate $(t = 0)$, all sine coefficients $B_n$ disappear, since the sine function itself is an odd function ⇒ $\sin(-\alpha) = -\sin(\alpha)$: | + | *If the time signal $x(t)$ is an even function ⇒ axis-symmetrical around the ordinate $(t = 0)$, all sine coefficients $B_n$ disappear, since the sine function itself is an odd function ⇒ $\sin(-\alpha) = -\sin(\alpha)$: |
:$$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$ | :$$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$ | ||
| − | *An odd function $x(t)$ is point symmetric around the coordinate origin $(t= 0; \ x =0)$. Therefore, all cosine coefficients $(A_n = 0)$ | + | *An odd function $x(t)$ is point-symmetric around the coordinate origin $(t= 0; \ x =0)$. Therefore, all cosine coefficients disappear here $(A_n = 0)$, since the cosine function itself is even. In this case, the DC coefficient is always $A_0=0$. |
:$$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$ | :$$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$ | ||
| − | *If a function without a | + | *If a function without a DC signal component is present $(A_0 = 0)$ and if this function is odd within a period ⇒ $x(t) = -x(t - T_0/2)$, then only odd multiples of the basic frequency are present in the Fourier series representation. For the coefficients with an even index, however, the following always applies: |
:$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$ | :$$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$ | ||
| − | *If all coefficients $A_n$ and $B_n$ with even-numbered index $(n = 2, \ 4, \ 6, \text{...})$ equals zero and the coefficient $A_0 \neq 0$, then the symmetry property mentioned in the last point refers to the DC component and applies: | + | *If all coefficients $A_n$ and $B_n$ with even-numbered index $(n = 2, \ 4, \ 6, \text{...})$ equals zero and the coefficient $A_0 \neq 0$, then the symmetry property mentioned in the last point refers to the DC component and applies: |
:$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | :$$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$ | ||
| − | + | <u>Remark:</u> Several of the named symmetry properties can be fulfilled at the same time. | |
| − | |||
| − | |||
| − | [[File:EN_Sig_T_2_4_S3.png|right|frame|Symmetry | + | {{GraueBox|TEXT= |
| − | + | [[File:EN_Sig_T_2_4_S3.png|right|frame|Symmetry properties of the Fourier coefficients]] | |
| + | |||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
| − | The | + | The mentioned properties are now illustrated by three signal waveforms: |
| − | *$x_1(t)$ is an | + | *$x_1(t)$ is an averaging function ⇒ $A_0 \ne 0$ and it is also even, which is accordingly exclusively determined by cosine coefficients $A_n$ ⇒ $B_n = 0$. |
| − | *In contrast, the odd function $x_2(t)$ all $A_n | + | *In contrast, with the odd function $x_2(t)$ all $A_n \ ( n \ge 0)$ are identical to zero. |
| − | *Also the odd function $x_3(t)$ contains only sine coefficients, but because of $x_3(t) = -x_3(t - T_0/2)$ exclusively for odd | + | *Also the odd function $x_3(t)$ contains only sine coefficients, but because of $x_3(t) = -x_3(t - T_0/2)$ exclusively for odd $n$–values. |
| − | ==Complex Fourier | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | The first part of the following $($German-language$)$ learning video explained the symmetry properties of the Fourier coefficients: | ||
| + | |||
| + | :[[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|»Eigenschaften der Fourierreihe«]] ⇒ "Properties and accuracy of Fourier series".}} | ||
| + | |||
| + | ==Complex Fourier series== | ||
<br> | <br> | ||
| − | As shown | + | As shown in the section [[Signal_Representation/Harmonic_Oscillation#Representation_with_cosine_and_sine_components|»Representation with cosine and sine components«]] in case of a harmonic oscillation any periodic signal |
| − | |||
:$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | :$$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$ | ||
| Line 163: | Line 183: | ||
These modified Fourier coefficients have the following properties: | These modified Fourier coefficients have the following properties: | ||
| − | *The '''DC coefficient'''& | + | *The »'''DC coefficient'''« $C_0$ is identical with $A_0$. |
| − | |||
| − | |||
| + | *The »'''magnitude coefficient'''« read with $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$. | ||
| − | With the & | + | *For the »'''phase coefficient'''« applies: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$). |
| + | |||
| + | |||
| + | With the »Eulerian relationship« $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ we get a second representation variant of Fourier series, which starts from the complex exponential function. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | The '''complex Fourier series''' of a periodic signal x(t) is as follows | + | The »'''complex Fourier series'''« of a periodic signal $x(t)$ is as follows: |
:$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | :$$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$ | ||
| − | Here $D_n$ denote the '''complex Fourier coefficients''', which | + | Here $D_n$ denote the »'''complex Fourier coefficients'''«, which can be calculated as follows $($valid for $n \neq 0)$: |
| − | *from the cosine coefficients $A_n$ and the sine coefficients $B_n$, | + | *from the cosine coefficients $A_n$ and the sine coefficients $B_n$: |
| − | *from the magnitude coefficients $C_n$ and the phase coefficients $\varphi_n | + | :$$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n),$$ |
| − | + | *from the magnitude coefficients $C_n$ and the phase coefficients $\varphi_n$: | |
| − | + | :$$D_n = 1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$}} | |
| − | |||
| − | |||
| − | :$$D_n | ||
| Line 190: | Line 209: | ||
:$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | :$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$ | ||
| − | As long as the integration interval $T_0$ is preserved, it can be shifted randomly as with the coefficients $A_n$ and $B_n$ | + | As long as the integration interval $T_0$ is preserved, it can be shifted randomly as with the coefficients $A_n$ and $B_n$, e.g. from $t = 0$ to $t = T_0$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ The coefficient $D_0 = A_0$ is always real. For the complex coefficients with negative | + | $\text{Conclusion:}$ The coefficient $D_0 = A_0$ is always real. For the complex coefficients with negative index $(n < 0)$ applies: |
:$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | :$$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$}} | ||
| − | ==Periodic | + | ==Periodic signal spectrum== |
<br> | <br> | ||
| − | Starting from the complex Fourier series | + | Starting from the complex Fourier series |
:$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | :$$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$ | ||
| − | and the [[Signal_Representation/ | + | and the [[Signal_Representation/Fourier_Transform_Theorems#Shifting_Theorem|»shifting theorem«]] $($for the frequency domain$)$ one gets the following spectrum for the periodic signal $x(t)$: |
:$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | :$$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | ||
This means: | This means: | ||
| − | * | + | *The $($amplitude$)$ spectrum of a periodic signal with period duration $T_0$ is a »'''line spectrum'''« for integer multiples of the basic frequency $f_0 = 1/T_0$. |
| − | * | + | |
| − | * | + | *The »'''DC signal component'''« returns a »Dirac delta function« at $f=0$ with the impulse weight $A_0$. |
| − | + | ||
| + | *There are also Dirac delta functions $\delta(f \pm n \cdot f_0)$ at the multiples of $f_0$, | ||
| + | |||
| + | :*where $\delta(f - n \cdot f_0)$ denotes a Dirac delta function at $f= n \cdot f_0$ $($namely in the positive frequency domain) | ||
| + | :*and $\delta(f + n \cdot f_0)$ denotes a Dirac at the frequency $f= -n \cdot f_0$ $($in the negative frequency domain$)$. | ||
| + | *The impulse weights for $n \ne 0$ are generally complex. | ||
| − | + | ||
| + | These statements will now be illustrated by two examples. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 4:}$ | $\text{Example 4:}$ | ||
| − | + | We consider as in [[Signal_Representation/Harmonic_Oscillation#Time_domain_representation|$\text{Example 1}$]] two periodic rectangular signals, each with period duration $T_0$ and basic frequency $f_0=1/T_0$. | |
| − | + | The upper signal | |
| − | + | ||
:$$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$ | :$$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$ | ||
| + | [[File:P_ID528__Sig_T_2_4_S6_neu.png|right|frame|Spectrum of a periodic rectangular signal]] | ||
| − | + | is an even $($German: "gerade" ⇒ "$\rm g$"$)$ function, composed of different cosine parts. | |
| − | + | Therefore: | |
| − | + | *The corresponding spectral function $X_{\rm g}(f)$ is thus purely real. | |
| − | + | ::<u>Reason:</u> As described in the section [[Signal_Representation/Harmonic_Oscillation#Representation_with_cosine_and_sine_components|»Spectral Representation of a cosine signal«]] the basic wave returns two Dirac delta functions at $\pm f_0$, each weighted with $2/\pi$. | |
| − | |||
| + | *This weighting corresponds to the $($generally complex$)$ Fourier coefficients $D_1 = D_{ - 1}^\ast$, which are only real in the special case of an even function. | ||
| − | [ | + | *Other Dirac delta functions are available in |
| + | :*$\pm 3f_0$ $($negative$)$, | ||
| + | |||
| + | :*$\pm 5f_0$ $($positive$)$, | ||
| + | |||
| + | :*$\pm 7f_0$ $($negative$)$, etc. | ||
| + | |||
| + | *All phase values $\varphi_n$ are either zero or $\pi$ due to the alternating signs. | ||
| + | <br clear=all> | ||
| + | ⇒ The function $x_{\rm u}(t)$ shown below is odd $($German: "ungerade" ⇒ "$\rm u$"$)$: | ||
| + | |||
| + | :$$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$ | ||
| − | + | *As described in the section [[Signal_Representation/Harmonic_Oscillation#General_spectral_representation|»General Spectral Representation«]] the basic wave provides two Dirac delta functions | |
| + | :*at $+f_0$ $($weighted with $-\text{j}\cdot 2/\pi)$ resp. | ||
| − | :$$ | + | :*at $-f_0$ $($weighted with $+\text{j}\cdot 2/\pi)$. |
| − | + | *All other Dirac delta functions at $\pm 3f_0$, $\pm 5f_0$, ... are also purely imaginary and located in the same direction as the Dirac delta functions at $\pm f_0$. | |
| − | * | ||
| − | |||
| + | *The two magnitude spectra are equal: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.}} | ||
| − | ==The Gibbs | + | ==The Gibbs phenomenon== |
<br> | <br> | ||
| − | + | Not every periodic signal is suitable for the Fourier series. Some restrictions below: | |
| − | * | + | *An important condition for the convergence of the Fourier series is that the signal may only have a finite number of discontinuities per period. |
| − | * | + | |
| − | *In | + | *At those places $t=t_i$, where $x(t)$ has jumps, the series converges to the arithmetic mean value formed by the respective left and right boundary value. |
| − | * | + | |
| + | *In the surrounding area of such discontinuities, high-frequency oscillations usually occur in the series representation. This error is of principle kind, i.e. it could not be avoided too, if infinite summands would be considered. One speaks of the "Gibbs phenomenon", named after the physicist [https://en.wikipedia.org/wiki/Josiah_Willard_Gibbs $\text{Josiah Willard Gibbs}$]. | ||
| + | |||
| + | *An increase of $N$ reduces the erroneous range but not the maximum deviation between $x(t)$ and the Fourier series representation $x_N(t)$. The maximum error is independent of $N$ about $9\%$ of the jumping amplitude. | ||
| − | + | The Gibbs phenomenon and other interesting aspects of comparable effects are presented in the $($German-language$)$ learning video<br> »[[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]]« ⇒ "Properties and accuracy of the Fourier series". | |
| − | [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 5:}$ | $\text{Example 5:}$ | ||
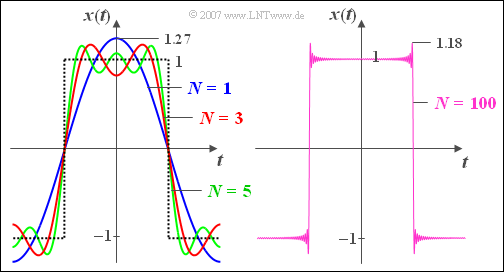
| − | + | The left graphic shows a dotted section of a periodic $\pm 1$ rectangular signal and the corresponding Fourier series representation with $N = 1$ $($blue$)$, $N = 3$ $($red$)$ and $N = 5$ $($green$)$ summands. | |
| − | |||
| − | |||
| + | [[File:P_ID2720__Sig_T_2_4_S7_neu.png|right|frame|On the Gibbs phenomenon]] | ||
| + | |||
| + | *The basic wave here has the amplitude value $4/\pi \approx 1.27$. | ||
| + | |||
| + | *Even with $N = 5$ $($this means because of $A_2 = A_4 = 0$ three "relevant" summands$)$ the Fourier series still differs significantly from the approximated rectangular signal, especially in the area of the edge. | ||
| − | |||
| − | From the right graphic you can see that the flank and the inner area are | + | |
| + | ⇒ From the right graphic you can see that the flank and the inner area are well reproduced with | ||
$N = 100$ but due to the Gibbs phenomenon there are still oscillations around $9\%$ at the jumping point. | $N = 100$ but due to the Gibbs phenomenon there are still oscillations around $9\%$ at the jumping point. | ||
| − | *Since the jump amplitudes here are equal to $2$ the maximum values are approximately $ | + | *Since the jump amplitudes here are equal to $2$ the maximum values are approximately $\pm1.18$. |
| − | *With $N = 1000$ the oscillations would be exactly the same size, but limited to a narrower space and possibly not recognizable with time | + | |
| + | *With $N = 1000$ the oscillations would be exactly the same size, but limited to a narrower space and possibly not recognizable with discrete-time representation.}} | ||
| − | ==Exercises for the | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.4:_Rectified_Cosine|Exercise 2.4: Rectified Cosine]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.4Z:_Triangular_Function|Exercise 2.4Z: Triangular Function]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5:_Half-Wave_Rectification|Exercise 2.5: Half-Wave Rectification]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5Z:_Square_Wave|Exercise 2.5Z: Square Wave]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.6:_Complex_Fourier_Series|Exercise 2.6: Complex Fourier Series]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.6Z:_Magnitude_and_Phase|Exercise 2.6Z: Magnitude and Phase]] |
Latest revision as of 17:21, 15 November 2023
Contents
General description
Every periodic function $x(t)$ can be developed into a trigonometric series called »Fourier series« in all areas, where it is continuous or has only finite discontinuities.
$\text{Definition:}$ The »Fourier series« of a periodic signal $x(t)$ is defined as follows:
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t).$$
Here the symbols denote the following definitions:
- $A_0$ the »constant component« of $x(t)$,
- $A_n$ the »cosine coefficients« with $n \ge 1$,
- $B_n$ the »sine coefficients« with $n \ge 1$,
- $\omega_0 = 2\pi/T_0$ the »basic circular frequency« of the periodic signal $(T_0$ is the period duration$)$.
If the Fourier series should exactly match the actual periodic signal $x(t)$, an infinite number of cosine and sine coefficients must generally be used for calculation.
- If the Fourier series is interrupted and only $N$ of $A_n$ and $B_n$ coefficients are used, then a slightly different plot of the function results except for some special cases:
- $$x_ N(t) =A_0+\sum^N_{n=1}A_ n \cdot \cos(n \omega_0 t)+\sum^N_{n=1} B_{n} \cdot \sin(n \omega_0 t).$$
- The relation between the periodic signal $x(t)$ and the Fourier series approximation $x_N(t)$ holds:
- $$x(t)=\lim_{N\to \infty} x_{N}(t).$$
- If $N \cdot f_0$ is the highest frequency occurring in the signal $x(t)$ then of course $x_N(t) = x(t)$.
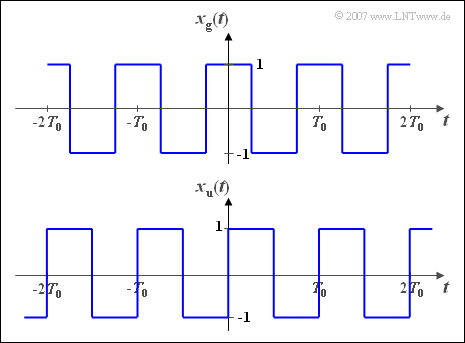
$\text{Example 1:}$ We consider two periodic rectangular signals $($"square waves"$)$, each with period duration $T_0$ and basic circular frequency $\omega_0 = 2\pi/T_0$.
- For the even $($German: "gerade" ⇒ $\rm g)$ time signal sketched above:
- $$x_{\rm g}(-t) = x_{\rm g}(t).$$
- The function shown below is odd $($German: "ungerade" ⇒ $\rm u)$:
- $$x_{\rm u}(-t) = -x_{\rm u}(t).$$
One finds the Fourier series representations of both signals in formularies:
- $$x_{\rm g}(t)=\frac{4}{\pi}\left [ \cos(\omega_0 t)-\frac{1}{3}\cdot \cos(3 \omega_0 t)+\frac{1}{5}\cdot\cos(5 \omega_0 t)- \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm}\right ],$$
- $$x_{\rm u}(t)=\frac{4}{\pi}\left [ \sin(\omega_0 t)+\frac{1}{3}\cdot\sin(3 \omega_0 t)+\frac{1}{5}\cdot\sin(5 \omega_0 t)+ \hspace{0.05cm}\text{...}\hspace{0.05cm} + \hspace{0.05cm}\text{...}\hspace{0.05cm} \right ].$$
- Because of the generally valid relationship
- $$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\, {-}\, \hspace{0.05cm}\text{...}\hspace{0.05cm} \, {+} \hspace{0.05cm}\text{...}\hspace{0.05cm}=\frac{\pi}{4},$$
- the amplitudes $($maximum values$)$ of the rectangular basic pulse result to $1$.
- This can also be verified using the signal curves in the graphic:
- $$x_{\rm g}(t = 0) = x_{\rm u}(t = T_0/4) = 1.$$
Calculation of the Fourier coefficients
The Fourier coefficient $A_0$ specifies the »direct current $\rm (DC)$ signal component« which can be determined by averaging over the signal course $x(t)$. Due to the periodicity, averaging over one period is sufficient:
- $$A_0=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\,{\rm d}t.$$
- The integration limits can also be selected from $t = 0$ to $t = T_0$ $($or over a differently defined period of equal length$)$.
- The determination of the Fourier coefficients $A_n$ and $B_n$ $(n \ge 1)$ is based on the property that cosine and sine functions are so-called »orthogonal functions«.
- For them the following applies:
- $$\int^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\cos(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \hspace{0.2cm} m=n,\atop \rm otherwise} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\sin(n\omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=\left \{{T_0/2\atop 0}{\rm\quad if \it \hspace{0.2cm} m=n,\atop \rm otherwise} \right.$$
- $$\int ^{+T_0/2}_{-T_0/2}\cos(n \omega_0 t)\cdot\sin(m \omega_0 t)\,{\rm d}t=0 \hspace{1.2cm} \rm for\ all \hspace{0.2cm} \it m, \ n.$$
$\text{Conclusion:}$ Considering these equations, the cosine coefficients $A_n$ and the sine coefficients $B_n$ result as follows
- $$A_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\cos(n \omega_0 t)\,{\rm d}t,$$
- $$B_{\it n}=\frac{2}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t)\cdot\sin(n \omega_0 t)\,{\rm d}t.$$
The following $($German-language$)$ learning video illustrates these equations:
»Zur Berechnung der Fourierkoeffizienten« ⇒ "Calculating the Fourier coefficients".
$\text{Example 2:}$ We consider the drawn periodic time function
- $$x(t)=0.4+0.6\cdot \cos(\omega_0 t)-0.3\cdot\sin(3 \omega_0 t).$$
- Since the integral of the cosine and sine functions over one period are identical to zero, the DC signal coefficient is
- $$A_0 = 0.4.$$
- One determines the cosine coefficient $A_1$ with following equation $($Integration limits from $t = 0$ to $t = T_0)$:
- $$ \begin{align*} A_{1}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4\cdot\cos(\omega_0 t)\,{\rm d}t + \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot\cos^2(\omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot\sin(3 \omega_0 t)\cdot \cos(\omega_0 t)\,{\rm d}t.\end{align*} $$
- The last integral is equal to zero due to orthogonality; the first one is zero too $($integral over one period$)$.
- Only the middle term contributes here to $A_1$, namely $2 - 0.6 - 0.5 = 0.6. $
- For all further $(n \ge 2)$ cosine coefficients all three integrals return the value zero, and thus $A_{n \hspace{0.05cm}\neq \hspace{0.05cm}1}=0$.
- To determine the sine coefficients $B_n$ using following equation:
- $$ \begin{align*} B_{\it n}=\frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.4 \cdot \sin(n \ \omega_0 t)\,{\rm d}t + \frac{2}{T_0} \cdot \int^{T_0}_{0}\hspace{-0.3cm}0.6\cdot \cos(\omega_0 t) \sin(n \omega_0 t)\,{\rm d}t - \frac{2}{T_0}\cdot \int^{T_0}_{0}\hspace{-0.3cm}0.3\cdot \sin(3 \omega_0 t) \sin(n \omega_0 t )\,{\rm d}t. \end{align*} $$
- For $n \hspace{0.05cm}\neq \hspace{0.05cm}3$ all three integral values are zero and therefore $B_{n \hspace{0.05cm}\neq \hspace{0.05cm}3} = 0.$
- On the other hand, for $n=3$ the last integral provides a contribution, and one gets for the sine coefficient
- $$B_3 = -0.3.$$
Exploitation of symmetries
Some insights into the Fourier coefficients $A_n$ and $B_n$ can already be read from the »symmetry properties« of the time function $x(t)$.
- If the time signal $x(t)$ is an even function ⇒ axis-symmetrical around the ordinate $(t = 0)$, all sine coefficients $B_n$ disappear, since the sine function itself is an odd function ⇒ $\sin(-\alpha) = -\sin(\alpha)$:
- $$B_n = 0 \hspace{0.4cm}(n = 1, \ 2, \ 3, \text{...}).$$
- An odd function $x(t)$ is point-symmetric around the coordinate origin $(t= 0; \ x =0)$. Therefore, all cosine coefficients disappear here $(A_n = 0)$, since the cosine function itself is even. In this case, the DC coefficient is always $A_0=0$.
- $$A_n = 0 \hspace{0.4cm}(n = 0, \ 1, \ 2, \ 3, \text{...}).$$
- If a function without a DC signal component is present $(A_0 = 0)$ and if this function is odd within a period ⇒ $x(t) = -x(t - T_0/2)$, then only odd multiples of the basic frequency are present in the Fourier series representation. For the coefficients with an even index, however, the following always applies:
- $$A_n = B_n = 0 \hspace{0.4cm}(n = 2, \ 4, \ 6, \text{...}).$$
- If all coefficients $A_n$ and $B_n$ with even-numbered index $(n = 2, \ 4, \ 6, \text{...})$ equals zero and the coefficient $A_0 \neq 0$, then the symmetry property mentioned in the last point refers to the DC component and applies:
- $$x(t) = 2 \cdot A_0 - x (t - T_0/2).$$
Remark: Several of the named symmetry properties can be fulfilled at the same time.
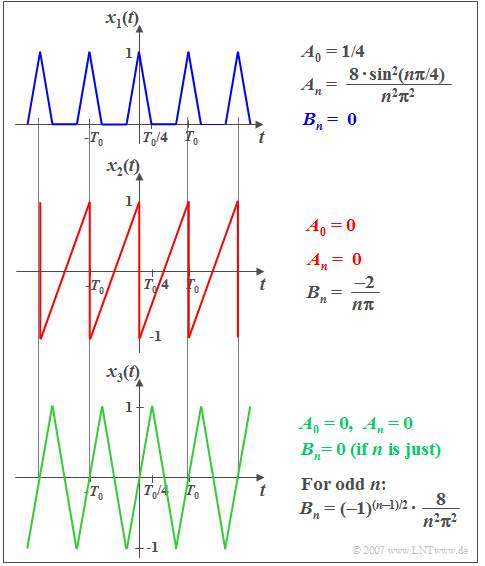
$\text{Example 3:}$ The mentioned properties are now illustrated by three signal waveforms:
- $x_1(t)$ is an averaging function ⇒ $A_0 \ne 0$ and it is also even, which is accordingly exclusively determined by cosine coefficients $A_n$ ⇒ $B_n = 0$.
- In contrast, with the odd function $x_2(t)$ all $A_n \ ( n \ge 0)$ are identical to zero.
- Also the odd function $x_3(t)$ contains only sine coefficients, but because of $x_3(t) = -x_3(t - T_0/2)$ exclusively for odd $n$–values.
The first part of the following $($German-language$)$ learning video explained the symmetry properties of the Fourier coefficients:
- »Eigenschaften der Fourierreihe« ⇒ "Properties and accuracy of Fourier series".
Complex Fourier series
As shown in the section »Representation with cosine and sine components« in case of a harmonic oscillation any periodic signal
- $$x(t) =A_0+\sum^{\infty}_{n=1}A_{\it n} \cdot\cos(n \omega_0 t)+\sum^{\infty}_{n=1} B_n \cdot \sin(n \omega_0 t)$$
can also be displayed using the magnitude and phase coefficients:
- $$x(t) =C_0+\sum^{\infty}_{n=1}C_{\it n} \cdot\cos(n \omega_0 t-\varphi_n).$$
These modified Fourier coefficients have the following properties:
- The »DC coefficient« $C_0$ is identical with $A_0$.
- The »magnitude coefficient« read with $n\ge 1$: $C_n = \sqrt{A_n^2 + B_n^2}$.
- For the »phase coefficient« applies: $\varphi_n = \arctan \hspace{0.05cm}(B_n/A_n$).
With the »Eulerian relationship« $\cos(x) + {\rm j} \cdot \sin(x) = {\rm e}^{{\rm j} \hspace{0.05cm}x}$ we get a second representation variant of Fourier series, which starts from the complex exponential function.
$\text{Definition:}$ The »complex Fourier series« of a periodic signal $x(t)$ is as follows:
- $$x(t)=\sum^{+\infty}_{ n=- \infty}D_n\cdot {\rm e}^{ {\rm j} \hspace{0.05cm} n \hspace{0.05cm}\omega_0\hspace{0.05cm} t}.$$
Here $D_n$ denote the »complex Fourier coefficients«, which can be calculated as follows $($valid for $n \neq 0)$:
- from the cosine coefficients $A_n$ and the sine coefficients $B_n$:
- $$D_n = 1/2\cdot (A_n - {\rm j}\cdot B_n),$$
- from the magnitude coefficients $C_n$ and the phase coefficients $\varphi_n$:
- $$D_n = 1/2\cdot C_n\cdot {\rm e}^{- {\rm j} \hspace{0.05cm} \varphi_n }$$
The complex Fourier coefficients can also be calculated directly using the following equation
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x(t) \cdot{\rm e}^{-\rm j \hspace{0.05cm}\it n \hspace{0.1cm}\omega_{\rm 0} \hspace{0.05cm}t}\, {\rm d}t.$$
As long as the integration interval $T_0$ is preserved, it can be shifted randomly as with the coefficients $A_n$ and $B_n$, e.g. from $t = 0$ to $t = T_0$.
$\text{Conclusion:}$ The coefficient $D_0 = A_0$ is always real. For the complex coefficients with negative index $(n < 0)$ applies:
- $$D_{- n}=D_n^{\hspace{0.05cm}\star} =1/2 \cdot (A_n+ {\rm j}\cdot B_n).$$
Periodic signal spectrum
Starting from the complex Fourier series
- $$x(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j \it n \omega_{\rm 0} t}$$
and the »shifting theorem« $($for the frequency domain$)$ one gets the following spectrum for the periodic signal $x(t)$:
- $$X(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
This means:
- The $($amplitude$)$ spectrum of a periodic signal with period duration $T_0$ is a »line spectrum« for integer multiples of the basic frequency $f_0 = 1/T_0$.
- The »DC signal component« returns a »Dirac delta function« at $f=0$ with the impulse weight $A_0$.
- There are also Dirac delta functions $\delta(f \pm n \cdot f_0)$ at the multiples of $f_0$,
- where $\delta(f - n \cdot f_0)$ denotes a Dirac delta function at $f= n \cdot f_0$ $($namely in the positive frequency domain)
- and $\delta(f + n \cdot f_0)$ denotes a Dirac at the frequency $f= -n \cdot f_0$ $($in the negative frequency domain$)$.
- The impulse weights for $n \ne 0$ are generally complex.
These statements will now be illustrated by two examples.
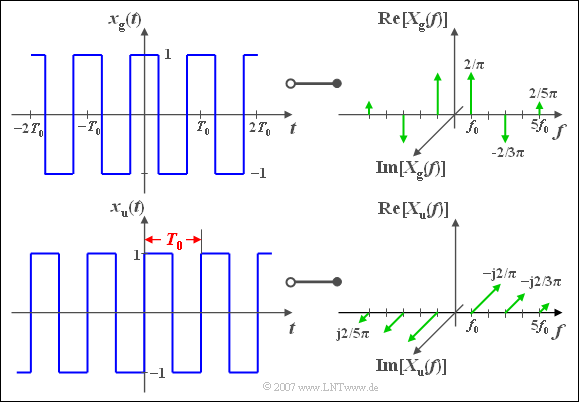
$\text{Example 4:}$ We consider as in $\text{Example 1}$ two periodic rectangular signals, each with period duration $T_0$ and basic frequency $f_0=1/T_0$. The upper signal
- $$x_{\rm g}(t)={4}/{\pi} \cdot \big[\cos(\omega_0 t) - {1}/{3} \cdot \cos(3\omega_0 t)+{1}/{5}\cdot \cos(5\omega_0 t) - \, \text{...} \, + \, \text{...} \big]$$
is an even $($German: "gerade" ⇒ "$\rm g$"$)$ function, composed of different cosine parts.
Therefore:
- The corresponding spectral function $X_{\rm g}(f)$ is thus purely real.
- Reason: As described in the section »Spectral Representation of a cosine signal« the basic wave returns two Dirac delta functions at $\pm f_0$, each weighted with $2/\pi$.
- This weighting corresponds to the $($generally complex$)$ Fourier coefficients $D_1 = D_{ - 1}^\ast$, which are only real in the special case of an even function.
- Other Dirac delta functions are available in
- $\pm 3f_0$ $($negative$)$,
- $\pm 5f_0$ $($positive$)$,
- $\pm 7f_0$ $($negative$)$, etc.
- All phase values $\varphi_n$ are either zero or $\pi$ due to the alternating signs.
⇒ The function $x_{\rm u}(t)$ shown below is odd $($German: "ungerade" ⇒ "$\rm u$"$)$:
- $$x_{\rm u}(t)={4}/{\pi} \cdot \big[\sin(\omega_0 t)+{1}/{3} \cdot \sin(3\omega_0 t)+{1}/{5} \cdot \sin(5\omega_0 t)+ \, \text{...}\big].$$
- As described in the section »General Spectral Representation« the basic wave provides two Dirac delta functions
- at $+f_0$ $($weighted with $-\text{j}\cdot 2/\pi)$ resp.
- at $-f_0$ $($weighted with $+\text{j}\cdot 2/\pi)$.
- All other Dirac delta functions at $\pm 3f_0$, $\pm 5f_0$, ... are also purely imaginary and located in the same direction as the Dirac delta functions at $\pm f_0$.
- The two magnitude spectra are equal: $\vert X_{\rm u}(f)\vert = \vert X_{\rm g}(f) \vert$.
The Gibbs phenomenon
Not every periodic signal is suitable for the Fourier series. Some restrictions below:
- An important condition for the convergence of the Fourier series is that the signal may only have a finite number of discontinuities per period.
- At those places $t=t_i$, where $x(t)$ has jumps, the series converges to the arithmetic mean value formed by the respective left and right boundary value.
- In the surrounding area of such discontinuities, high-frequency oscillations usually occur in the series representation. This error is of principle kind, i.e. it could not be avoided too, if infinite summands would be considered. One speaks of the "Gibbs phenomenon", named after the physicist $\text{Josiah Willard Gibbs}$.
- An increase of $N$ reduces the erroneous range but not the maximum deviation between $x(t)$ and the Fourier series representation $x_N(t)$. The maximum error is independent of $N$ about $9\%$ of the jumping amplitude.
The Gibbs phenomenon and other interesting aspects of comparable effects are presented in the $($German-language$)$ learning video
»Eigenschaften der Fourierreihendarstellung« ⇒ "Properties and accuracy of the Fourier series".
$\text{Example 5:}$ The left graphic shows a dotted section of a periodic $\pm 1$ rectangular signal and the corresponding Fourier series representation with $N = 1$ $($blue$)$, $N = 3$ $($red$)$ and $N = 5$ $($green$)$ summands.
- The basic wave here has the amplitude value $4/\pi \approx 1.27$.
- Even with $N = 5$ $($this means because of $A_2 = A_4 = 0$ three "relevant" summands$)$ the Fourier series still differs significantly from the approximated rectangular signal, especially in the area of the edge.
⇒ From the right graphic you can see that the flank and the inner area are well reproduced with $N = 100$ but due to the Gibbs phenomenon there are still oscillations around $9\%$ at the jumping point.
- Since the jump amplitudes here are equal to $2$ the maximum values are approximately $\pm1.18$.
- With $N = 1000$ the oscillations would be exactly the same size, but limited to a narrower space and possibly not recognizable with discrete-time representation.
Exercises for the chapter
Exercise 2.4: Rectified Cosine
Exercise 2.4Z: Triangular Function
Exercise 2.5: Half-Wave Rectification
Exercise 2.6: Complex Fourier Series
Exercise 2.6Z: Magnitude and Phase