Difference between revisions of "Theory of Stochastic Signals/Poisson Distribution"
| (18 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
{{Header | {{Header | ||
|Untermenü=Discrete Random Variables | |Untermenü=Discrete Random Variables | ||
| − | |Vorherige Seite=Binomial | + | |Vorherige Seite=Binomial Distribution |
| − | |Nächste Seite= | + | |Nächste Seite=Generation of Discrete Random Variables |
}} | }} | ||
==Probabilities of the Poisson distribution== | ==Probabilities of the Poisson distribution== | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Poisson distribution''' is a limiting case of the [[Theory_of_Stochastic_Signals/Binomial_Distribution#General_description_of_the_binomial_distribution|binomial distribution]], where | + | $\text{Definition:}$ The »'''Poisson distribution'''« is a limiting case of the [[Theory_of_Stochastic_Signals/Binomial_Distribution#General_description_of_the_binomial_distribution|»binomial distribution»]], where |
| − | *on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed, | + | *on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed, |
| − | *additionally, it is assumed that the product | + | |
| + | *additionally, it is assumed that the product has following value: | ||
| + | :$$I · p =\it λ.$$ | ||
| + | The parameter $\it \lambda $ gives the average number of »ones« in a fixed time unit and is called the »'''rate'''«. }} | ||
| − | |||
| + | $\text{Further, it should be noted:}$ | ||
| + | *In contrast to the binomial distribution $(0 ≤ μ ≤ I)$ here the random quantity can take on arbitrarily large $($integer, non-negative$)$ values. | ||
| − | + | *This means that the set of possible values is uncountable here. | |
| − | + | ||
| − | *This means that the set of possible values | + | *But since no intermediate values can occur, this is also called a »discrete distribution«. |
| − | *But since no intermediate values can occur, this is also called a | ||
{{BlueBox|TEXT= | {{BlueBox|TEXT= | ||
| − | $\text{Calculation rule:}$ | + | $\text{Calculation rule:}$ Considering above limit transitions for the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution|»probabilities of the binomial distribution«]], it follows for the »'''Poisson distribution probabilities'''«: |
| − | |||
| − | Considering above limit transitions for the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution| | ||
:$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | :$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | ||
| − | From this, after some algebraic transformations | + | From this, after some algebraic transformations: |
:$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$}} | :$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$}} | ||
| − | [[File: EN_Sto_T_2_4_S1_neu.png |frame| | + | {{GraueBox|TEXT= |
| − | + | [[File: EN_Sto_T_2_4_S1_neu.png |frame| Binomial and Poisson probabilities| right]] | |
| − | $\text{Example 1:}$ | + | $\text{Example 1:}$ In the graph on the right can be seen the probabilities of |
| − | * | + | *binomial distribution with $I =6$, $p = 0.4$, $($blue arrows and labels$)$ |
| − | * | + | |
| + | *Poisson distribution with $λ = 2.4$ $($red arrows and labels$)$. | ||
| − | can | + | You can recognize: |
| − | + | #Both distributions have the same mean $m_1 = 2.4$. | |
| − | + | #In the binomial distribution, all probabilities ${\rm Pr}(z > 6) \equiv 0$. | |
| − | + | #In the Poisson distribution the outer values are more probable than with the binomial distribution. | |
| + | #Random variables $z > 6$ are also possible with the Poisson distribution. | ||
| + | #But their probabilities are also rather small at the chosen rate. }} | ||
| − | == | + | ==Moments of the Poisson distribution== |
<br> | <br> | ||
| − | {{ | + | {{BlueBox|TEXT= |
| − | $\text{ | + | $\text{Calculation rule:}$ »'''Mean'''« and »'''standard deviation'''« are obtained directly from the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Moments_of_the_binomial_distribution|»corresponding equations of the binomial distribution«]] by twofold limiting: |
| − | |||
| − | |||
:$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | :$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | ||
:$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | :$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | ||
| − | + | From this it can be seen that with the Poisson distribution the variance is always | |
| + | :$$σ^2 = m_1 = λ.$$ }} | ||
| − | [[File: P_ID616__Sto_T_2_4_S2neu.png |frame| | + | {{GraueBox|TEXT= |
| − | + | [[File: P_ID616__Sto_T_2_4_S2neu.png |frame| Moments of the Poisson distribution | right]] | |
| − | $\text{ | + | $\text{Example 2:}$ As in $\text{Example 1}$, here we compare |
| + | *the binomial distribution with $I =6$, $p = 0.4$, $($blue arrows and labels$)$ and | ||
| + | |||
| + | *the Poisson distribution with $λ = 2.4$ $($red arrows and labels$)$. | ||
| − | |||
| − | |||
| − | |||
| + | One can see from the accompanying sketch: | ||
| − | + | #Both distributions have exactly the same mean $m_1 = 2.4$. | |
| + | #For the red Poisson distribution, the standard deviation $σ ≈ 1.55$. | ||
| + | #In contrast, for the blue binomial distribution, the standard deviation is only $σ = 1.2$. | ||
| − | |||
| − | |||
| − | |||
| + | ⇒ With the interactive HTML 5/JavaScript applet [[Applets:Binomial_and_Poisson_Distribution_(Applet)|»Binomial and Poisson Distribution»]], you can | ||
| + | *determine the probabilities and moments of the Poisson distribution for any $λ$-values | ||
| + | |||
| + | *and visualize the similarities and differences compared to the binomial distribution.}} | ||
| − | |||
| + | ==Comparison of binomial distribution vs. Poisson distribution== | ||
| + | <br> | ||
| + | Now both the similarities and the differences between binomial and Poisson distributed random variables shall be worked out again. | ||
| − | + | The »'''binomial distribution'''« is suitable for the description of such stochastic events, which are characterized by a given clock $T$. For example, for [[Examples_of_Communication_Systems/General_Description_of_ISDN|'''ISDN''']] $($»Integrated Services Digital Network»$)$ with $64 \ \rm kbit/s$ ⇒ the clock time $T \approx 15.6 \ \rm µ s$. | |
| − | + | [[File: EN_Sto_T_2_4_S3.png |right|frame| Binomial distribution $($blue$)$ vs. Poisson distribution $($red$)$]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | #'''Binary events only occur in this time grid'''. Such events are, for example, error-free $(e_i = 0)$ or errored $(e_i = 1)$ transmission of individual symbols. | ||
| + | #The binomial distribution now allows statistical statements about the number of transmission errors to be expected in a longer time interval $T_{\rm I} = I ⋅ T$ according to the upper diagram of the graph $($time marked in blue$)$. | ||
| − | |||
| − | + | Also the »'''Poisson distribution'''« makes statements about the number of occurring binary events in a finite time interval: | |
| − | + | #If one assumes the same observation period $T_{\rm I}$ and increases the number $I$ of subintervals more and more, then the clock time $T$, at which a new binary event $(0$ or $1)$ can occur, becomes smaller and smaller. In the limiting case: $T \to 0$. | |
| − | + | #This means: In the Poisson distribution, '''the binary events are possible''' not only at discrete time points given by a time grid, but '''at any time'''. | |
| − | + | #In order to obtain during time $T_{\rm I}$ on average exactly as many on average »ones« as in the binomial distribution $($in the example: six$)$, the characteristic probability related to the infinitesimally small interval $T$ must tend to $p = {\rm Pr}( e_i = 1)=0$. | |
| − | == | + | ==Applications of the Poisson distribution== |
<br> | <br> | ||
| − | + | The Poisson distribution is the result of a so-called [https://en.wikipedia.org/wiki/Poisson_point_process »Poisson process«]. Such a process is often used as a model for sequences of events that may occur at random times. Examples of such events include | |
| − | + | #the prediction of equipmente failure – an important task in reliability theory, | |
| − | + | #the shot noise in optical transmission, and | |
| − | + | #the start of telephone calls in a switching center $($»teletraffic engineering«$)$. | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ If ninety switching requests per minute $(λ = 1.5 \text{ per second})$ are received by a switching center on a long–term average, the probabilities $p_\mu$ that exactly $\mu$ connections occur in any one-second period: |
:$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | :$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | ||
| − | + | This gives the numerical values $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc. | |
| + | |||
| + | From this, further characteristics can be derived: | ||
| + | *The distance $τ$ between two connection requests satisfies the [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#One-sided_exponential_distribution|»exponential distribution«]]. | ||
| + | |||
| + | *So, the mean time interval between two connection requests is ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.}} | ||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5:_"Binomial"_or_"Poisson"%3F|Exercise 2.5: "Binomial" or "Poisson"?]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.5Z:_Flower_Meadow|Exercise 2.5Z: Flower Meadow]] |
{{Display}} | {{Display}} | ||
Latest revision as of 18:58, 7 February 2024
Contents
Probabilities of the Poisson distribution
$\text{Definition:}$ The »Poisson distribution« is a limiting case of the »binomial distribution», where
- on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed,
- additionally, it is assumed that the product has following value:
- $$I · p =\it λ.$$
The parameter $\it \lambda $ gives the average number of »ones« in a fixed time unit and is called the »rate«.
$\text{Further, it should be noted:}$
- In contrast to the binomial distribution $(0 ≤ μ ≤ I)$ here the random quantity can take on arbitrarily large $($integer, non-negative$)$ values.
- This means that the set of possible values is uncountable here.
- But since no intermediate values can occur, this is also called a »discrete distribution«.
$\text{Calculation rule:}$ Considering above limit transitions for the »probabilities of the binomial distribution«, it follows for the »Poisson distribution probabilities«:
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
From this, after some algebraic transformations:
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
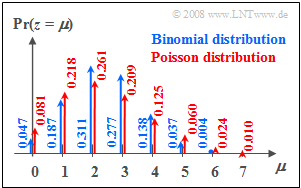
$\text{Example 1:}$ In the graph on the right can be seen the probabilities of
- binomial distribution with $I =6$, $p = 0.4$, $($blue arrows and labels$)$
- Poisson distribution with $λ = 2.4$ $($red arrows and labels$)$.
You can recognize:
- Both distributions have the same mean $m_1 = 2.4$.
- In the binomial distribution, all probabilities ${\rm Pr}(z > 6) \equiv 0$.
- In the Poisson distribution the outer values are more probable than with the binomial distribution.
- Random variables $z > 6$ are also possible with the Poisson distribution.
- But their probabilities are also rather small at the chosen rate.
Moments of the Poisson distribution
$\text{Calculation rule:}$ »Mean« and »standard deviation« are obtained directly from the »corresponding equations of the binomial distribution« by twofold limiting:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$
- $$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
From this it can be seen that with the Poisson distribution the variance is always
- $$σ^2 = m_1 = λ.$$
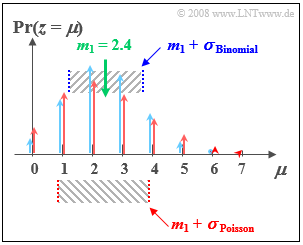
$\text{Example 2:}$ As in $\text{Example 1}$, here we compare
- the binomial distribution with $I =6$, $p = 0.4$, $($blue arrows and labels$)$ and
- the Poisson distribution with $λ = 2.4$ $($red arrows and labels$)$.
One can see from the accompanying sketch:
- Both distributions have exactly the same mean $m_1 = 2.4$.
- For the red Poisson distribution, the standard deviation $σ ≈ 1.55$.
- In contrast, for the blue binomial distribution, the standard deviation is only $σ = 1.2$.
⇒ With the interactive HTML 5/JavaScript applet »Binomial and Poisson Distribution», you can
- determine the probabilities and moments of the Poisson distribution for any $λ$-values
- and visualize the similarities and differences compared to the binomial distribution.
Comparison of binomial distribution vs. Poisson distribution
Now both the similarities and the differences between binomial and Poisson distributed random variables shall be worked out again.
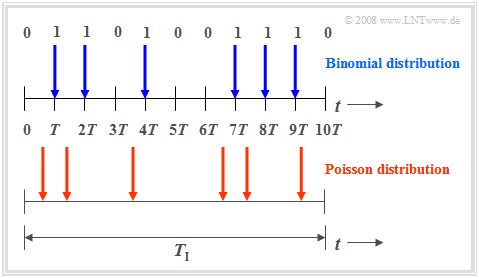
The »binomial distribution« is suitable for the description of such stochastic events, which are characterized by a given clock $T$. For example, for ISDN $($»Integrated Services Digital Network»$)$ with $64 \ \rm kbit/s$ ⇒ the clock time $T \approx 15.6 \ \rm µ s$.
- Binary events only occur in this time grid. Such events are, for example, error-free $(e_i = 0)$ or errored $(e_i = 1)$ transmission of individual symbols.
- The binomial distribution now allows statistical statements about the number of transmission errors to be expected in a longer time interval $T_{\rm I} = I ⋅ T$ according to the upper diagram of the graph $($time marked in blue$)$.
Also the »Poisson distribution« makes statements about the number of occurring binary events in a finite time interval:
- If one assumes the same observation period $T_{\rm I}$ and increases the number $I$ of subintervals more and more, then the clock time $T$, at which a new binary event $(0$ or $1)$ can occur, becomes smaller and smaller. In the limiting case: $T \to 0$.
- This means: In the Poisson distribution, the binary events are possible not only at discrete time points given by a time grid, but at any time.
- In order to obtain during time $T_{\rm I}$ on average exactly as many on average »ones« as in the binomial distribution $($in the example: six$)$, the characteristic probability related to the infinitesimally small interval $T$ must tend to $p = {\rm Pr}( e_i = 1)=0$.
Applications of the Poisson distribution
The Poisson distribution is the result of a so-called »Poisson process«. Such a process is often used as a model for sequences of events that may occur at random times. Examples of such events include
- the prediction of equipmente failure – an important task in reliability theory,
- the shot noise in optical transmission, and
- the start of telephone calls in a switching center $($»teletraffic engineering«$)$.
$\text{Example 3:}$ If ninety switching requests per minute $(λ = 1.5 \text{ per second})$ are received by a switching center on a long–term average, the probabilities $p_\mu$ that exactly $\mu$ connections occur in any one-second period:
- $$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$
This gives the numerical values $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc.
From this, further characteristics can be derived:
- The distance $τ$ between two connection requests satisfies the »exponential distribution«.
- So, the mean time interval between two connection requests is ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.
Exercises for the chapter
Exercise 2.5: "Binomial" or "Poisson"?