Aufgaben:Exercise 4.12Z: White Gaussian Noise

• Return to book

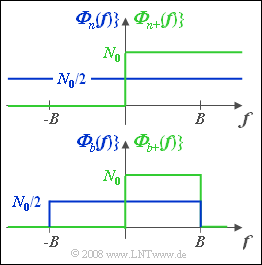
Man bezeichnet ein Rauschsignal n(t) als weiß, wenn darin alle spektralen Anteile ohne Bevorzugung von irgendwelchen Frequenzen enthalten sind.

• Das physikalische, nur für positive Frequenzen f definierte Leistungsdichtespektrum Φ_n+(f) ist konstant (gleich N₀) und reicht frequenzmäßig bis ins Unendliche.

• Φ_n+(f) ist in der oberen Grafik grün dargestellt. Das Pluszeichen im Index soll anzeigen, dass die Funktion nur für positive Werte von f gültig ist.

• Zur mathematischen Beschreibung verwendet man meist das zweiseitige Leistungsdichtespektrum Φ_n(f). Hier gilt für alle Frequenzen von –∞ bis +∞ (blauer Kurvenzug im oberen Bild):

$${\it \Phi}_n (f) ={N_0}/{2}.$$

Im unteren Bild sind die beiden Leistungsdichtespektren Φ_b(f) und Φ_b+(f) eines bandbegrenzten weißen Rauschsignals b(t) dargestellt. Es gilt mit der einseitigen Bandbreite B:

$${\it \Phi}_b(f)=\left\{ {N_0/2\atop 0}{\hspace{0.5cm} {\rm f\ddot{u}r}\quad |f|\le B \atop {\rm sonst}}\right.,$$

$${\it \Phi}_{b+}(f)=\left\{ {N_0\atop 0}{\hspace{0.5cm} {\rm f\ddot{u}r}\quad 0 \le f\le B \atop {\rm sonst}}\right..$$

Bei der Rechnersimulation von Rauschvorgängen muss stets von bandbegrenztem Rauschen ausgegangen werden, da hier nur zeitdiskrete Vorgänge behandelt werden können. Dazu muss das Abtasttheorem (siehe Buch Signaldarstellung, Kapitel 5.1) eingehalten werden. Dieses sagt aus, dass die Bandbreite B gemäß dem Stützstellenabstand T_A der Simulation eingestellt werden muss.

Gehen Sie in der gesamten Aufgabe von folgenden Zahlenwerten aus:

• Die Rauschleistungsdichte (bezogen auf den Widerstand 1 Ω) beträgt N₀ = 4 · 10^–14 V²/Hz.

• Die (einseitige) Bandbreite des bandbegrenzten weißen Rauschens beträgt B = 100 MHz.

Hinweis: Die Aufgabe bezieht sich auf Kapitel 4.4 und Kapitel 4.5.
Die Eigenschaften von weißem Rauschen sind in einem Lernvideo zusammengefasst:

Fragebogen

1

Welche Aussagen treffen bei einem weißen Rauschsignal n(t) immer zu? Begründen Sie Ihre Antworten.

	Die AKF φn(τ) hat einen si-förmigen Verlauf.
	Die AKF φn(τ) ist ein Dirac bei τ = 0 mit Gewicht N0/2.
	Im mathematisch strengen Sinn gibt es kein weißes Rauschen.
	Thermisches Rauschen kann stets als weiß angenähert werden.
	Weißes Rauschen ist stets gaußverteilt.

2

Berechnen Sie die AKF φ_b(τ) des bandbegrenzten Zufallssignals b(t). Welcher Wert ergibt sich für τ = 0?

$B = 100 MHz: \ \ \ \phi_b(\tau\ =\ 0)$ = $.10^{-6}\ V^2$

3

Wie groß ist der Effektivwert dieses Rauschsignals?

$\sigma_b$ = $.10^{-3}\ V$

4

Welcher Abtastabstand T_A ist (mindestens) zu wählen, wenn das Signal b(t) zur zeitdiskreten Simulation von weißem Rauschen eingesetzt wird?

$T_A$ = $ns$

5

Gehen Sie nun vom Abtastabstand T_A = 1 ns aus. Welche der Aussagen treffen dann für zwei aufeinanderfolgende Abtastwerte des Signals b(t) zu?

	Die Abtastwerte sind unkorreliert.
	Die Abtastwerte sind positiv korreliert.
	Die Abtastwerte sind negativ korreliert.

Musterlösung

Solution

1.  Richtig sind die Lösungsvorschläge 2, 3 und 4. Die Autokorrelationsfunktion (AKF) ist nämlich die Fouriertransformierte des Leistungsdichtespektrums (LDS). Dabei gilt:

$${\it \Phi}_n (f) = \frac {N_0}{2} \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} \varphi_n (\tau)=\frac {N_0}{2} \cdot {\rm \delta} ( \tau).$$

„Echt” weißes Rauschen gibt es in der Physik allerdings nicht, da ein solches eine unendlich große Signalleistung aufweisen müsste (das Integral über das LDS und der AKF-Wert bei τ = 0 sind jeweils unendlich groß). Thermisches Rauschen hat bis zu Frequenzen von etwa 6000 GHz ein konstantes LDS. Da alle (derzeitigen) Übertragungssysteme in einem sehr viel niedrigeren Frequenzbereich arbeiten, kann man thermisches Rauschen mit guter Näherung als „weiß” bezeichnen.

Die statistische Eigenschaft „weiß” sagt nichts über die Amplitudenverteilung aus, die allein durch die Wahrscheinlichkeitsdichtefunktion (WDF) festgelegt ist. Betrachtet man beispielsweise die Phase eines bandpassförmigen Signals als die stochastische Größe, so wird diese oft als gleichverteilt zwischen 0 und 2π modelliert. Bestehen zwischen den jeweiligen Phasenwinkeln zu unterschiedlichen Zeiten keine statistischen Bindungen, so ist auch dieser Zufallsprozess „weiß”.

2.  Das LDS ist ein Rechteck der Breite 2B und der Höhe N₀/2.

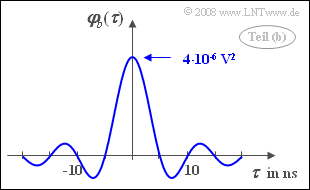
Die Fourierrücktransformation ergibt eine si-Funktion:

$$\varphi_b(\tau) = N_0 \cdot B \cdot {\rm si} (2 \pi B \tau).$$

Der AKF-Wert an der Stelle τ = 0 entspricht der Rechteckfläche: (N₀/2) · 2B = 4 · 10^–6 V².

3.  Der AKF-Wert an der Stelle τ = 0 ergibt die Leistung; die Wurzel hieraus bezeichnet man als den Effektivwert: σ_b = 2 mV.

4.  Die bei (b) berechnete AKF hat Nullstellen im äquidistanten Abstand von 1/(2B) = 5 ns = T_A. Das bedeutet: Es bestehen somit keine statistischen Bindungen zwischen den beiden Signalwerten b(t) und b(t + ν · T_A), wobei ν alle ganzzahligen Werte annehmen kann.

5.  Der AKF-Wert bei τ = T_A = 1 ns beträgt

$$\varphi_b(\tau = T_{\rm A}) = {\rm 4 \cdot 10^{-6} \hspace{0.1cm}V^2 \cdot si (\pi/5) \approx 3.742 \cdot 10^{-6} \hspace{0.1cm}V^2}$$

und ist damit positiv. Dieses Ergebnis besagt: Zwei um T_A = 1 Nanosekunde auseinander liegende Signalwerte sind positiv korreliert  ⇒  Lösungsvorschlag 2. Ist b(t) positiv und groß, dann ist mit großer Wahrscheinlichkeit auch b(t + 1 ns) positiv und groß. Dagegen besteht zwischen b(t) und b(t + 7 ns) eine negative Korrelation: Ist b(t) positiv, so ist b(t + 7 ns) wahrscheinlich negativ.