Difference between revisions of "Aufgaben:Exercise 1.3: Calculating with Complex Numbers"

From LNTwww
 
(54 intermediate revisions by 5 users not shown)
Line 1: Line 1:
−
{{quiz-Header|Buchseite=Signaldarstellung/Zum Rechnen mit komplexen Zahlen}}
+
{{quiz-Header|Buchseite=Signal_Representation/Calculating_With_Complex_Numbers}}
  
−
[[File:P_ID800_Sig_A_1_3.png|right|Zahlen in der komplexen Ebene]]
+
[[File:P_ID800_Sig_A_1_3.png|right|frame|Considered numbers <br>in the complex plane]]
−
Nebenstehende Grafik zeigt einige Punkte in der komplexen Ebene, nämlich
+
The diagram to the right shows some points in the complex plane, namely
 
   
 
   
−
$$z_1 = {\rm e}^{-{\rm j} 45^{ \circ}}, $$
+
:$$z_1 = {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}, $$
−
$$z_2 = 2 \cdot{\rm e}^{{\rm j} 135^{ \circ}},$$
+
:$$z_2 = 2 \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}},$$
−
$$z_3 = -{\rm j} .$$
+
:$$z_3 = -{\rm j} .$$
 
   
 
   
−
Im Verlauf dieser Aufgabe werden noch folgende komplexe Größen betrachtet:
+
In the course of this task, the following complex quantities will be considered:
−
$$z_4 = z_2^2 + z_3^2,$$
+
:$$z_4 = z_2^2 + z_3^2,$$
−
$$z_5 = 1/z_2,$$
+
:$$z_5 = 1/z_2,$$
−
$$z_6 = \sqrt{z_3},$$
+
:$$z_6 = \sqrt{z_3},$$
−
$$z_7 = {\rm e}^{z_2},$$
+
:$$z_7 = {\rm e}^{\hspace{0.05cm}z_2},$$
−
$$z_8 = {\rm e}^{z_2} + {\rm e}^{z_2^{\star}}.$$
+
:$$z_8 = {\rm e}^{\hspace{0.05cm}z_2} + {\rm e}^{\hspace{0.05cm}z_2^{\star}}.$$
 
   
 
   
  
−
''Hinweise:''
 
−
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Prinzip_der_Nachrichtenübertragung|Prinzip der Nachrichtenübertragung]].
 
−
*Sollte die Eingabe des Zahlenwertes &bdquo;0&rdquo; erforderlich sein, so geben Sie bitte &bdquo;0.&rdquo; ein.
 
  
−
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.3. Die Thematik wird auch in folgendem Lernvideo behandelt:
 
−
[http://{{SERVERNAME}}/mediawiki/swf_files/Buch1/komplex.swf Rechnen mit komplexen Zahlen (Dauer 11:52)]
 
  
 +
''Notes:''
 +
*This exercise belongs to the chapter&nbsp;[[Signal_Representation/Calculating_With_Complex_Numbers|Calculating with Complex Numbers]].
 +
*The topic of this task is also covered in the (German language) learning video <br> &nbsp; &nbsp;  &nbsp;[[Rechnen_mit_komplexen_Zahlen_(Lernvideo)|Rechnen mit komplexen Zahlen]] &nbsp; &rArr; &nbsp; "Arithmetic operations involving complex numbers".
  
  
  
−
===Fragebogen zu "A1.3 Rechnen mit komplexen Zahlen"===
+
===Questions===
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Welche der folgenden Gleichungen sind zutreffend?
+
{Which of the following equations are true?
 
|type="[]"}
 
|type="[]"}
−
+ <math>2 \cdot z_1 + z_2 =0</math>
+
+ <math>2 \cdot z_1 + z_2 =0.</math>
−
+ <math>z_1^{\ast} \cdot z_2 +2=0</math>
+
+ <math>z_1^{\ast} \cdot z_2 +2=0.</math>
−
- <math>(z_1/z_2) \cdot z_3</math> ist rein reell.
+
- <math>(z_1/z_2) \cdot z_3</math> is purely real.
  
  
−
{Welchen Wert besitzt die Zufallsgröße <math>z_4 = z_2^2 + z_3^2 = x_4 + j \cdot y_4</math>?
+
{What is the value of the complex quantity&nbsp; <math>z_4 = z_2^2 + z_3^2 = x_4 + {\rm j} \cdot y_4</math>?
 
|type="{}"}
 
|type="{}"}
−
<math> x_4 = </math> { -1 }
+
<math> x_4 \ =\  </math> { -1.01--0.99 }
−
<math> y_4 = </math> { -4 }
+
<math> y_4 \ =\  </math> { -4.01--3.99 }
  
  
−
{Berechnen Sie die komplexe Größe <math>z_5 = \frac{1}{z_2} = x_5 + j \cdot y_5</math>
+
{Calculate the complex quantity&nbsp; <math>z_5 = 1/z_2 = x_5 + {\rm j} \cdot y_5</math>.
 
|type="{}"}
 
|type="{}"}
−
<math> x_4 = </math> { -0.4--0.3  }
+
<math> x_5 \ =\  </math> { -0.36--0.35 }
−
<math> y_4 = </math> { -0.4--0.3  }
+
<math> y_5  \ =\  </math> { -0.36--0.35 }
  
−
 
+
{<math>z_6</math>&nbsp; is the square root of&nbsp; <math>z_3</math>.&nbsp; Therefore <math>z_6</math>&nbsp; has two solutions with the magnitude&nbsp; <math>|z_6| = 1</math>. <br>Give the two possible phase angles of&nbsp; <math>z_6</math>&nbsp;.
−
{<math>z_6</math> hat als Quadratwurzel von <math>z_3</math> zwei Lösungen; beide mit dem Betrag <math>|z_6| = 1</math>. Geben Sie die beiden möglichen Phasenwinkel von <math>z_6</math> an.
 
 
|type="{}"}
 
|type="{}"}
−
<math> \phi_6 </math>  (zwischen 0 Grad  und 180 Grad) = { 135  }
+
<math> \phi_6 \ ({\rm between\hspace{0.1cm} 0^{\circ} \hspace{0.1cm}and \hspace{0.1cm} +\hspace{-0.15cm}180^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ </math>    { 133-137 } $\ \text{deg}$
−
<math> \phi_6 </math>  (zwischen -180 Grad und 0 Grad) = { -45 }
+
<math> \phi_6 \ ({\rm between\hspace{0.1cm} - \hspace{-0.15cm}180^{\circ} \hspace{0.1cm}and \hspace{0.1cm} 0^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ </math>  { -47--43 } $\ \text{deg}$
  
  
−
{Berechnen Sie <math>z_7 = e^{z_2} = x_7 + j \cdot y_7</math>
+
{Calculate&nbsp; <math>z_7 = {\rm e}^{z_2} = x_7 + {\rm j} \cdot y_7</math>.
 
|type="{}"}
 
|type="{}"}
−
<math> x_7 = </math> { 0.03-0.04 }
+
<math> x_7 \ =\  </math> { 0.03-0.04 }
−
<math> y_7 = </math> { 0.2-0.3 }
+
<math> y_7 \ =\ </math> { 0.2-0.3 }
  
  
−
{Geben Sie die komplexe Größe <math>z_8 = e^{z_2} + e^{z_2^{\ast}} = x_8 + j \cdot y_8</math>
+
{Calculate the complex quantity&nbsp; <math>z_8 = {\rm e}^{z_2} + {\rm e}^{z_2^{\ast}} = x_8 + {\rm j}\cdot y_8</math>&nbsp;.
 
|type="{}"}
 
|type="{}"}
−
<math> x_8 = </math> { 0.07-0.08 }
+
<math> x_8 \ =\  </math> { 0.07-0.08 }
−
<math> y_8 = </math> { 0 }
+
<math> y_8 \ =\  </math> { 0. }
  
  
 
</quiz>
 
</quiz>
  
−
===Musterlösung zu "A1.3 Rechnen mit komplexen Zahlen"===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''1.''' Entsprechend den Angaben gilt mit dem Satz von Euler:
+
'''(1)'''&nbsp; Correct are the<u> solutions 1 and 2</u>:
 +
*The following applies with&nbsp; [[Signal_Representation/Calculating_With_Complex_Numbers#Representation_by_Amplidute_and_Phase|Euler's theorem]]:&nbsp;
  
−
<math>2 \cdot z_1 + z_2 = 2 \cdot cos(45^{\circ}) - 2j \cdot sin(45^{\circ}) - 2 \cdot cos(45^{\circ}) + 2j \cdot sin(45^{\circ}) = 0</math>
+
::<math>2 \cdot z_1 + z_2 = 2 \cdot \cos(45^{ \circ}) - 2 \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \sin(45^{ \circ})- 2 \cdot \cos(45^{ \circ}) + 2\cdot {\rm j} \cdot\sin(45^{ \circ}) = 0.</math>
  
−
Der zweite Vorschlag ist ebenfalls richtig, da
+
*The second option is also correct, because
 +
::<math>z_1^{\star} \cdot z_2 = 1 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}} \cdot 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}} = 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{
 +
\circ}}= -2.</math>
  
−
<math>z_1^{\ast} \cdot z_2 = 1 \cdot e^{j45^{\circ} \cdot 2 \cdot e^{j135^{\circ}}=-2}</math>
+
*In contrast, the third option is wrong. The division of&nbsp; <math>z_1</math> and <math>z_2</math>&nbsp; yields:&nbsp;
 +
 +
::<math>\frac{z_1}{z_2} = \frac{{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}}{2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}}} =
 +
0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{
 +
\circ}}= -0.5.</math>
  
−
Dagegen ist der dritte Vorschlag falsch. Die Division von <math>z_1</math> und <math>z_2</math> liefert:
+
*The multiplication by&nbsp; <math>z_3 = -{\rm j} </math>&nbsp; leads to the result&nbsp; ${\rm j}/2$, i.e. to a purely imaginary quantity.  
−
 
−
<math>\frac{z_1}{z_2}=\frac{e^{-j45^{\circ}}}{2 \cdot e^{j135^{\circ}}} = 0.5 \cdot e^{-j180^{\circ}} = -0.5</math>
 
  
−
Die Multiplikation mit <math>z_3 = -j</math> führt zum Ergebnis j/2, also zu einer rein imaginären Größe. Richtig sind also die Lösungsvorschläge 1 und 2. 
 
  
  
−
'''2.''' Das Quadrat von <math>z_2</math> hat den Betrag <math>|z_2|^{2}</math> und die Phase <math>2 \cdot \phi_2</math>:
+
'''(2)'''&nbsp; The square of&nbsp; <math>z_2</math>&nbsp; has the magnitude&nbsp; <math>|z_2|^{2}</math>&nbsp; and the Phase&nbsp; <math>2 \cdot \phi_2</math>:&nbsp;
  
−
<math>z_2^2 = 2^2 \cdot e^{j270^{\circ}} = 4 \cdot e^{-j90^{\circ}} = -4j</math>
+
::<math>z_2^2 = 2^2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 270^{ \circ}}= 4 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}=-4 \cdot {\rm j}.</math>
 
   
 
   
−
Entsprechend gilt für das Quadrat von <math>z_3</math>:
+
*Accordingly, the following applies to the square of&nbsp; <math>z_3</math>:
 
   
 
   
−
<math>z_3^2=(-j)^2 = -1</math>
+
::<math>z_3^2 = (-{\rm j})^2 = -1.</math>
−
Somit ist <math>x_4</math> = –1 und <math>y_4</math> = –4
+
*Thus&nbsp; <math>x_4 =\underline{ –1}</math>&nbsp;  and&nbsp; <math>y_4 = \underline{–4}.</math>
−
 
 
−
 
 
−
'''3.''' Durch Anwendung der Divisionsregel erhält man:
 
−
 
 
−
<math>z_5 = \frac{1}{z_2} = \frac{1}{2 \cdot e^{j135^{\circ}}} = 0.5 \cdot e^{-j135^{\circ}} = 0.5 \cdot (cos(-135^{\circ}) + j \cdot sin(-135^{\circ}))</math>
 
−
<math>\Rightarrow x_5 = y_5 = - \frac{\sqrt{2}}{4}= -0.354</math>
 
  
  
−
'''4.''' Die angegeben Beziehung für <math>z_6</math> kann wie folgt umgeformt werden:
 
  
−
<math>z_6^2 = z_3 = e^{-90^{\circ}}</math>
+
'''(3)'''&nbsp; By applying the division rule one obtains:&nbsp;
  
−
Man erkennt, dass es zwei Möglichkeiten für <math>z_6</math> gibt, die diese Gleichung erfüllen:
+
::<math>z_5 = {1}/{z_2} = \frac{1}{2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}}}= 0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{
 +
\circ}} = 0.5 \cdot \big[ \cos (- 135^{ \circ}) + {\rm j} \cdot \sin (- 135^{
 +
\circ})\big]</math>
 +
::<math>\Rightarrow \ x_5 = - {\sqrt{2}}/{4}\hspace{0.15cm}\underline{= -0.354},\hspace{0.5cm} y_5 = x_5 \hspace{0.15cm}\underline{= -0.354}.</math>
  
−
<math>z_6(1.Loesung) = \frac{z_2}{2}= 1 \cdot e^{j135^{\circ}} \Rightarrow  \phi_6 = 135^{\circ}</math>
 
  
−
<math>z_6(2.Loesung) = z_1= 1 \cdot e^{-j45^{\circ}} \Rightarrow \phi_6 = -45^{\circ}</math>
+
'''(4)'''&nbsp; The given relation for&nbsp; <math>z_6</math>&nbsp; can be transformed as follows:&nbsp; <math>z_6^2 = {z_3} = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}.</math>
  
 +
*We can see that there are two possibilities for&nbsp; <math>z_6</math>&nbsp; that satisfy this equation: &nbsp;
  
−
'''5.''' Die komplexe Größe <math>z_2</math> lautet in Realteil/imaginärteildarstellung:
+
::<math>z_6 \hspace{0.1cm}{\rm (1.\hspace{0.1cm} solution)}\hspace{0.1cm} = \frac{z_2}{2} = 1 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}}
 +
\hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6 \hspace{0.15cm}\underline{= 135^{
 +
\circ}}, </math>
  
−
<math>z_2 = x_2 + j \cdot y_2 = -\sqrt{2} + j \cdot \sqrt{2}</math>
+
::<math>z_6 \hspace{0.1cm}{\rm (2.\hspace{0.1cm} solution)}\hspace{0.1cm} = {z_1} = 1 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}45^{ \circ}}
 +
\hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6  \hspace{0.15cm}\underline{=-45^{
 +
\circ}}.</math>
  
−
Damit ergibt sich für die komplexe Exponentialfunktion:
 
  
−
<math>z_7 = e^{-\sqrt{2}+j \cdot \sqrt{2}} = e^{-\sqrt{2}} \cdot (cos(\sqrt{2} + j \cdot sin(\sqrt{2})</math>
+
'''(5)'''&nbsp; The complex quantity&nbsp; <math>z_2</math>&nbsp; in real part/imaginary part representation is:&nbsp;
  
−
Mit
+
::<math>z_2 = x_2 + {\rm j} \cdot y_2 = -\sqrt{2} + {\rm j} \cdot\sqrt{2}.</math>
  
−
<math>e^{-\sqrt{2}} = 0.243, \quad cos(\sqrt{2}) = 0.156, \quad sin(\sqrt{2}) = 0.988</math>
+
*This results in the following for the complex exponential function:
  
−
erhält man somit:
+
::<math>z_7 =  {\rm e}^{-\sqrt{2} + {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2}}= {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2})\big].</math>
  
−
<math>z_7 = 0.243 \cdot (0.156 + j \cdot 0.988) = 0.038 + j \cdot 0.24</math>
+
*Thus with&nbsp; <math>{\rm e}^{-\sqrt{2} } = 0.243, \hspace{0.4cm}  \cos (\sqrt{2}) = 0.156, \hspace{0.4cm} \sin (\sqrt{2}) = 0.988</math>&nbsp; one obtains:&nbsp;
  
 +
::<math>z_7 = 0.243 \cdot \left( 0.156 + {\rm j} \cdot 0.988\right) \hspace{0.15cm}\underline{= 0.038 + {\rm j} \cdot 0.24}.</math>
  
−
'''6.''' Ausgehend vom Ergebnis 4. erhält man für <math>z_8</math>:
 
  
−
<math>z_8 = e^{-\sqrt{2}} \cdot (cos(\sqrt{2}) + j \cdot sin(\sqrt{2}) + cos(\sqrt{2}) - j \cdot (\sqrt{2}))</math>
 
  
−
<math>2 \cdot e^{-\sqrt{2}} \cdot cos(\sqrt{2}) = 2 \cdot x_7</math>
+
'''(6)'''&nbsp; Starting from the result of subtask&nbsp; '''(4)'''&nbsp; one obtains for <math>z_8</math>:&nbsp;
  
−
<math>\Rightarrow x_8 = 0.076, \quad y_8 =0</math>
+
::<math>z_8 = {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2}) + \cos (\sqrt{2}) - {\rm j} \cdot \sin
 +
(\sqrt{2})\big]
 +
= 2 \cdot {\rm e}^{-\sqrt{2} } \cdot \cos (\sqrt{2}) = 2 \cdot x_7 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x_8 \hspace{0.15cm}\underline{= 0.076}, \hspace{0.4cm}y_8\hspace{0.15cm}\underline{ = 0}.</math>
 
{{ML-Fuß}}
 
{{ML-Fuß}}
  
 
__NOEDITSECTION__
 
__NOEDITSECTION__
−
[[Category:Aufgaben zu Signaldarstellung|^1. Grundbegriffe der Nachrichtentechnik^]]
+
[[Category:Signal Representation: Exercises|^1.3 Calculating with Complex Numbers^]]

Latest revision as of 13:28, 24 May 2021

Considered numbers
in the complex plane

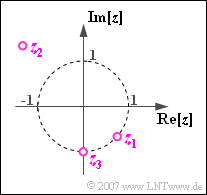
The diagram to the right shows some points in the complex plane, namely

$$z_1 = {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}, $$
$$z_2 = 2 \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}},$$
$$z_3 = -{\rm j} .$$

In the course of this task, the following complex quantities will be considered:

$$z_4 = z_2^2 + z_3^2,$$
$$z_5 = 1/z_2,$$
$$z_6 = \sqrt{z_3},$$
$$z_7 = {\rm e}^{\hspace{0.05cm}z_2},$$
$$z_8 = {\rm e}^{\hspace{0.05cm}z_2} + {\rm e}^{\hspace{0.05cm}z_2^{\star}}.$$



Notes:


Questions

1

Which of the following equations are true?

\(2 \cdot z_1 + z_2 =0.\)
\(z_1^{\ast} \cdot z_2 +2=0.\)
\((z_1/z_2) \cdot z_3\) is purely real.

2

What is the value of the complex quantity  \(z_4 = z_2^2 + z_3^2 = x_4 + {\rm j} \cdot y_4\)?

\( x_4 \ =\ \)

\( y_4 \ =\ \)

3

Calculate the complex quantity  \(z_5 = 1/z_2 = x_5 + {\rm j} \cdot y_5\).

\( x_5 \ =\ \)

\( y_5 \ =\ \)

4

\(z_6\)  is the square root of  \(z_3\).  Therefore \(z_6\)  has two solutions with the magnitude  \(|z_6| = 1\).
Give the two possible phase angles of  \(z_6\) .

\( \phi_6 \ ({\rm between\hspace{0.1cm} 0^{\circ} \hspace{0.1cm}and \hspace{0.1cm} +\hspace{-0.15cm}180^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ \)

$\ \text{deg}$
\( \phi_6 \ ({\rm between\hspace{0.1cm} - \hspace{-0.15cm}180^{\circ} \hspace{0.1cm}and \hspace{0.1cm} 0^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ \)

$\ \text{deg}$

5

Calculate  \(z_7 = {\rm e}^{z_2} = x_7 + {\rm j} \cdot y_7\).

\( x_7 \ =\ \)

\( y_7 \ =\ \)

6

Calculate the complex quantity  \(z_8 = {\rm e}^{z_2} + {\rm e}^{z_2^{\ast}} = x_8 + {\rm j}\cdot y_8\) .

\( x_8 \ =\ \)

\( y_8 \ =\ \)


Solution

Solution

(1)  Correct are the solutions 1 and 2:

\[2 \cdot z_1 + z_2 = 2 \cdot \cos(45^{ \circ}) - 2 \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \sin(45^{ \circ})- 2 \cdot \cos(45^{ \circ}) + 2\cdot {\rm j} \cdot\sin(45^{ \circ}) = 0.\]
  • The second option is also correct, because
\[z_1^{\star} \cdot z_2 = 1 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}} \cdot 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}} = 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{ \circ}}= -2.\]
  • In contrast, the third option is wrong. The division of  \(z_1\) and \(z_2\)  yields: 
\[\frac{z_1}{z_2} = \frac{{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}}{2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}}} = 0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{ \circ}}= -0.5.\]
  • The multiplication by  \(z_3 = -{\rm j} \)  leads to the result  ${\rm j}/2$, i.e. to a purely imaginary quantity.


(2)  The square of  \(z_2\)  has the magnitude  \(|z_2|^{2}\)  and the Phase  \(2 \cdot \phi_2\): 

\[z_2^2 = 2^2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 270^{ \circ}}= 4 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}=-4 \cdot {\rm j}.\]
  • Accordingly, the following applies to the square of  \(z_3\):
\[z_3^2 = (-{\rm j})^2 = -1.\]
  • Thus  \(x_4 =\underline{ –1}\)  and  \(y_4 = \underline{–4}.\)


(3)  By applying the division rule one obtains: 

\[z_5 = {1}/{z_2} = \frac{1}{2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}}}= 0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}} = 0.5 \cdot \big[ \cos (- 135^{ \circ}) + {\rm j} \cdot \sin (- 135^{ \circ})\big]\]
\[\Rightarrow \ x_5 = - {\sqrt{2}}/{4}\hspace{0.15cm}\underline{= -0.354},\hspace{0.5cm} y_5 = x_5 \hspace{0.15cm}\underline{= -0.354}.\]


(4)  The given relation for  \(z_6\)  can be transformed as follows:  \(z_6^2 = {z_3} = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}.\)

  • We can see that there are two possibilities for  \(z_6\)  that satisfy this equation:  
\[z_6 \hspace{0.1cm}{\rm (1.\hspace{0.1cm} solution)}\hspace{0.1cm} = \frac{z_2}{2} = 1 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}} \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6 \hspace{0.15cm}\underline{= 135^{ \circ}}, \]
\[z_6 \hspace{0.1cm}{\rm (2.\hspace{0.1cm} solution)}\hspace{0.1cm} = {z_1} = 1 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}45^{ \circ}} \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6 \hspace{0.15cm}\underline{=-45^{ \circ}}.\]


(5)  The complex quantity  \(z_2\)  in real part/imaginary part representation is: 

\[z_2 = x_2 + {\rm j} \cdot y_2 = -\sqrt{2} + {\rm j} \cdot\sqrt{2}.\]
  • This results in the following for the complex exponential function:
\[z_7 = {\rm e}^{-\sqrt{2} + {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2}}= {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2})\big].\]
  • Thus with  \({\rm e}^{-\sqrt{2} } = 0.243, \hspace{0.4cm} \cos (\sqrt{2}) = 0.156, \hspace{0.4cm} \sin (\sqrt{2}) = 0.988\)  one obtains: 
\[z_7 = 0.243 \cdot \left( 0.156 + {\rm j} \cdot 0.988\right) \hspace{0.15cm}\underline{= 0.038 + {\rm j} \cdot 0.24}.\]


(6)  Starting from the result of subtask  (4)  one obtains for \(z_8\): 

\[z_8 = {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2}) + \cos (\sqrt{2}) - {\rm j} \cdot \sin (\sqrt{2})\big] = 2 \cdot {\rm e}^{-\sqrt{2} } \cdot \cos (\sqrt{2}) = 2 \cdot x_7 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x_8 \hspace{0.15cm}\underline{= 0.076}, \hspace{0.4cm}y_8\hspace{0.15cm}\underline{ = 0}.\]

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_1.3:_Calculating_with_Complex_Numbers&oldid=38331"
  • Powered by MediaWiki