Difference between revisions of "Aufgaben:Exercise 1.3Z: Calculating with Complex Numbers II"
From LNTwww
| (26 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Calculating_With_Complex_Numbers}} |
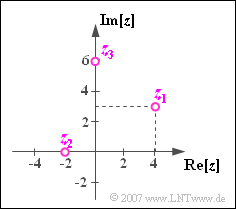
| − | [[File:P_ID802__Sig_Z_1_3.png|right| | + | [[File:P_ID802__Sig_Z_1_3.png|right|frame|Considered numbers <br>in the complex plane]] |
| − | + | The following three complex quantities are shown in the complex plane to the right: | |
| − | : $$z_1 = 4 + 3{\rm j},$$ | + | : $$z_1 = 4 + 3\cdot {\rm j},$$ |
: $$ z_2 = -2 ,$$ | : $$ z_2 = -2 ,$$ | ||
| − | : $$z_3 = 6{\rm j} .$$ | + | : $$z_3 = 6\cdot{\rm j} .$$ |
| − | + | Within the framework of this task, the following quantities are to be calculated: | |
: $$z_4 = z_1 \cdot z_1^{\star},$$ | : $$z_4 = z_1 \cdot z_1^{\star},$$ | ||
: $$z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2},$$ | : $$z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2},$$ | ||
| Line 13: | Line 13: | ||
: $$z_7 = {z_3}/{z_1}.$$ | : $$z_7 = {z_3}/{z_1}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Calculating_With_Complex_Numbers|Calculating with Complex Numbers]]. | ||
| + | *The topic of this task is also covered in the (German language) learning video <br> [[Rechnen_mit_komplexen_Zahlen_(Lernvideo)|Rechnen mit komplexen Zahlen]] ⇒ "Arithmetic operations involving complex numbers". | ||
| + | *Enter the phase values in the range of $-\hspace{-0.05cm}180^{\circ} < \phi ≤ +180^{\circ}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Enter the magnitude and phase of $z_1$ . |
|type="{}"} | |type="{}"} | ||
| − | $|z_1|$ | + | $|z_1|\ = \ ${ 5 3% } |
| − | $\phi_1$ | + | $\phi_1\ = \ $ { 36.9 3% } $\hspace{0.2cm}\text{deg}$ |
| − | { | + | {What is $z_4 = z_1 \cdot z_1^{\star} = x_4 + \text{j} \cdot y_4$? |
|type="{}"} | |type="{}"} | ||
| − | $x_4$ | + | $x_4\ = \ $ { 25 3% } |
| − | $y_4$ | + | $y_4\ = \ $ { 0. } |
| − | { | + | {Calculate $z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2} = x_5 + {\rm j} \cdot y_5$ . |
|type="{}"} | |type="{}"} | ||
| − | $x_5$ | + | $x_5\ = \ $ { 0. } |
| − | $y_5$ | + | $y_5\ = \ $ { 0. } |
| − | { | + | {Specify the magnitude and phase of $z_6 = z_1 \cdot z_2$ $($range $\pm 180^{\circ})$. |
|type="{}"} | |type="{}"} | ||
| − | $|z_6|$ | + | $|z_6|\ = \ $ { 10 3% } |
| − | $\phi_6$ | + | $\phi_6\ = \ $ { -145--140 } $\hspace{0.2cm}\text{deg}$ |
| − | { | + | {What is the phase value of the purely imaginary number $z_3$? |
|type="{}"} | |type="{}"} | ||
| − | $\phi_3$ | + | $\phi_3 \ = \ $ { 90 3% } $\hspace{0.2cm}\text{deg}$ |
| − | { | + | {Calculate the magnitude and phase of $z_7 = z_3/z_1$ $($range $\pm 180^{\circ})$. |
|type="{}"} | |type="{}"} | ||
| − | $|z_7|$ | + | $|z_7| \ = \ $ { 1.2 3% } |
| − | $\phi_7$ | + | $\phi_7 \ = \ $ { 53.1 3% } $\hspace{0.2cm}\text{deg}$ |
| − | |||
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The magnitude can be calculated according to the [https://en.wikipedia.org/wiki/Pythagoras Pythagorean ] theorem: |
:$$|z_1| = \sqrt{x_1^2 + y_1^2}= \sqrt{4^2 + 3^2}\hspace{0.15cm}\underline{ = 5}.$$ | :$$|z_1| = \sqrt{x_1^2 + y_1^2}= \sqrt{4^2 + 3^2}\hspace{0.15cm}\underline{ = 5}.$$ | ||
| − | + | *For the phase angle, the following applies according to the page [[Signal_Representation/Calculating_With_Complex_Numbers#Representation_by_Magnitude_and_Phase|Representation by Magnitude and Phase]]: | |
:$$\phi_1 = \arctan \frac{y_1}{x_1}= \arctan \frac{3}{4}\hspace{0.15cm}\underline{ = 36.9^{\circ}}.$$ | :$$\phi_1 = \arctan \frac{y_1}{x_1}= \arctan \frac{3}{4}\hspace{0.15cm}\underline{ = 36.9^{\circ}}.$$ | ||
| − | '''2 | + | |
| + | |||
| + | '''(2)''' Multiplying $z_1$ by its conjugate complex $z_1^{\star}$ yields the purely real quantity $z_4$, as the following equations show: | ||
:$$z_4 = (x_1 + {\rm j} \cdot y_1)(x_1 - {\rm j} \cdot y_1)= {x_1^2 + | :$$z_4 = (x_1 + {\rm j} \cdot y_1)(x_1 - {\rm j} \cdot y_1)= {x_1^2 + | ||
y_1^2}= |z_1|^2 = 25,$$ | y_1^2}= |z_1|^2 = 25,$$ | ||
| − | :$$z_4 = |z_1| \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi_1} \cdot |z_1| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_1}= |z_1|^2 = 25 | + | :$$z_4 = |z_1| \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi_1} \cdot |z_1| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_1}= |z_1|^2 = 25\hspace{0.3cm} |
| − | + | \Rightarrow\hspace{0.3cm} x_4 \hspace{0.1cm}\underline{= 25}, \hspace{0.25cm}y_4 \hspace{0.15cm}\underline{= 0}.$$ | |
| − | '''3 | + | |
| − | :$$x_5 = x_1 + 2 \cdot x_2 - | + | |
| − | :$$y_5 = y_1 + 2 \cdot y_2 - | + | '''(3)''' By dividing into real and imaginary part one can write: |
| − | '''4 | + | :$$x_5 = x_1 + 2 \cdot x_2 - {x_3}/{2} = 4 + 2 \cdot(-2) -0 \hspace{0.15cm}\underline{= 0},$$ |
| + | :$$y_5 = y_1 + 2 \cdot y_2 - {y_3}/{2} = 3 + 2 \cdot 0 - \frac{6}{2} \hspace{0.1cm}\underline{=0}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' If one writes $z_2$ as magnitude and phase ⇒ $|z_2| = 2, \ \phi_2 = 180^{\circ}$, one obtains for the product: | ||
:$$|z_6| = |z_1| \cdot |z_2|= 5 \cdot 2 \hspace{0.15cm}\underline{= 10},$$ | :$$|z_6| = |z_1| \cdot |z_2|= 5 \cdot 2 \hspace{0.15cm}\underline{= 10},$$ | ||
:$$\phi_6 = \phi_1 + \phi_2 = 36.9^{\circ} + 180^{\circ} = | :$$\phi_6 = \phi_1 + \phi_2 = 36.9^{\circ} + 180^{\circ} = | ||
216.9^{\circ}\hspace{0.15cm}\underline{= -143.1^{\circ}}.$$ | 216.9^{\circ}\hspace{0.15cm}\underline{= -143.1^{\circ}}.$$ | ||
| − | '''5 | + | |
| − | :$$\ | + | |
| − | \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \ | + | '''(5)''' The phase is $\phi_3 = 90^{\circ}$ (see graph above). This can be formally proven: |
| + | :$$\phi_3 = \arctan \left( \frac{6}{0}\right) = \arctan (\infty) | ||
| + | \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_3 \hspace{0.15cm}\underline{= 90^{ | ||
\circ}}.$$ | \circ}}.$$ | ||
| − | '''6 | + | |
| + | |||
| + | '''(6)''' First, the more inconvenient solution: | ||
:$$z_7 = \frac{z_3}{z_1}= \frac{6{\rm j}}{4 + 3{\rm j}} = \frac{6{\rm j}\cdot(4 - 3{\rm j})}{(4 + 3{\rm j})\cdot (4 - 3{\rm j})} = | :$$z_7 = \frac{z_3}{z_1}= \frac{6{\rm j}}{4 + 3{\rm j}} = \frac{6{\rm j}\cdot(4 - 3{\rm j})}{(4 + 3{\rm j})\cdot (4 - 3{\rm j})} = | ||
| − | \frac{18 +24{\rm j}}{25} = 1.2 \cdot{\rm e}^{{\rm j} 53.1^{ \circ}}.$$ | + | \frac{18 +24{\rm j}}{25} = 1.2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 53.1^{ \circ}}.$$ |
| − | + | *An easier way of solving the problem is: | |
:$$|z_7| = \frac{|z_3|}{|z_1|} = \frac{6}{5}\hspace{0.15cm}\underline{=1.2}, \hspace{0.3cm}\phi_7 = \phi_3 - \phi_1 = 90^{\circ} - 36.9^{\circ} | :$$|z_7| = \frac{|z_3|}{|z_1|} = \frac{6}{5}\hspace{0.15cm}\underline{=1.2}, \hspace{0.3cm}\phi_7 = \phi_3 - \phi_1 = 90^{\circ} - 36.9^{\circ} | ||
\hspace{0.15cm}\underline{=53.1^{\circ}}.$$ | \hspace{0.15cm}\underline{=53.1^{\circ}}.$$ | ||
| Line 94: | Line 107: | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^1.3 Calculating with Complex Numbers |
| + | ^]] | ||
Latest revision as of 13:28, 24 May 2021
The following three complex quantities are shown in the complex plane to the right:
- $$z_1 = 4 + 3\cdot {\rm j},$$
- $$ z_2 = -2 ,$$
- $$z_3 = 6\cdot{\rm j} .$$
Within the framework of this task, the following quantities are to be calculated:
- $$z_4 = z_1 \cdot z_1^{\star},$$
- $$z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2},$$
- $$z_6 = z_1 \cdot z_2,$$
- $$z_7 = {z_3}/{z_1}.$$
Hints:
- This exercise belongs to the chapter Calculating with Complex Numbers.
- The topic of this task is also covered in the (German language) learning video
Rechnen mit komplexen Zahlen ⇒ "Arithmetic operations involving complex numbers". - Enter the phase values in the range of $-\hspace{-0.05cm}180^{\circ} < \phi ≤ +180^{\circ}$.
Questions
Solution
(1) The magnitude can be calculated according to the Pythagorean theorem:
- $$|z_1| = \sqrt{x_1^2 + y_1^2}= \sqrt{4^2 + 3^2}\hspace{0.15cm}\underline{ = 5}.$$
- For the phase angle, the following applies according to the page Representation by Magnitude and Phase:
- $$\phi_1 = \arctan \frac{y_1}{x_1}= \arctan \frac{3}{4}\hspace{0.15cm}\underline{ = 36.9^{\circ}}.$$
(2) Multiplying $z_1$ by its conjugate complex $z_1^{\star}$ yields the purely real quantity $z_4$, as the following equations show:
- $$z_4 = (x_1 + {\rm j} \cdot y_1)(x_1 - {\rm j} \cdot y_1)= {x_1^2 + y_1^2}= |z_1|^2 = 25,$$
- $$z_4 = |z_1| \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi_1} \cdot |z_1| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_1}= |z_1|^2 = 25\hspace{0.3cm} \Rightarrow\hspace{0.3cm} x_4 \hspace{0.1cm}\underline{= 25}, \hspace{0.25cm}y_4 \hspace{0.15cm}\underline{= 0}.$$
(3) By dividing into real and imaginary part one can write:
- $$x_5 = x_1 + 2 \cdot x_2 - {x_3}/{2} = 4 + 2 \cdot(-2) -0 \hspace{0.15cm}\underline{= 0},$$
- $$y_5 = y_1 + 2 \cdot y_2 - {y_3}/{2} = 3 + 2 \cdot 0 - \frac{6}{2} \hspace{0.1cm}\underline{=0}.$$
(4) If one writes $z_2$ as magnitude and phase ⇒ $|z_2| = 2, \ \phi_2 = 180^{\circ}$, one obtains for the product:
- $$|z_6| = |z_1| \cdot |z_2|= 5 \cdot 2 \hspace{0.15cm}\underline{= 10},$$
- $$\phi_6 = \phi_1 + \phi_2 = 36.9^{\circ} + 180^{\circ} = 216.9^{\circ}\hspace{0.15cm}\underline{= -143.1^{\circ}}.$$
(5) The phase is $\phi_3 = 90^{\circ}$ (see graph above). This can be formally proven:
- $$\phi_3 = \arctan \left( \frac{6}{0}\right) = \arctan (\infty) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_3 \hspace{0.15cm}\underline{= 90^{ \circ}}.$$
(6) First, the more inconvenient solution:
- $$z_7 = \frac{z_3}{z_1}= \frac{6{\rm j}}{4 + 3{\rm j}} = \frac{6{\rm j}\cdot(4 - 3{\rm j})}{(4 + 3{\rm j})\cdot (4 - 3{\rm j})} = \frac{18 +24{\rm j}}{25} = 1.2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 53.1^{ \circ}}.$$
- An easier way of solving the problem is:
- $$|z_7| = \frac{|z_3|}{|z_1|} = \frac{6}{5}\hspace{0.15cm}\underline{=1.2}, \hspace{0.3cm}\phi_7 = \phi_3 - \phi_1 = 90^{\circ} - 36.9^{\circ} \hspace{0.15cm}\underline{=53.1^{\circ}}.$$