Difference between revisions of "Aufgaben:Exercise 5.5: Fast Fourier Transform"
| (20 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fast_Fourier_Transform_(FFT) |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sig_A_5_5.png|right|frame|FFT algorithm for $N=8$]] |
| − | + | The graph shows the signal flow diagram of the Fast Fourier Transform $\rm (FFT)$ for $N = 8$. | |
| + | |||
| + | The associated spectral coefficients $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ are determined from the time coefficients $d(0), \hspace{0.03cm}\text{...} \hspace{0.1cm}, d(7)$. The following applies to these with $0 ≤ μ ≤ 7$: | ||
| − | $$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} | + | :$$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} |
| − | d(\nu) \cdot {w}^{\nu \hspace{0. | + | d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.05cm} \cdot |
\hspace{0.05cm}\mu}\hspace{0.05cm},$$ | \hspace{0.05cm}\mu}\hspace{0.05cm},$$ | ||
| − | + | where the complex rotation factor $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot | |
| + | \hspace{0.05cm}2\pi /N}$ is to be used, i.e. $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm}\pi /4}$ für $N = 8$. | ||
| + | |||
| + | *The alternating $±1$ sequence $\langle\hspace{0.05cm} d(ν)\hspace{0.05cm}\rangle$ is applied to the input. | ||
| + | *After the bit reversal operation, this results in the sequence $\langle \hspace{0.05cm}b(\kappa)\hspace{0.05cm}\rangle$. | ||
| + | |||
| + | |||
| + | It holds that $b(κ) = d(ν)$, if $ν$ is represented as a dual number and the resulting three bits are written as $κ$ in reverse order. For example | ||
| + | * $ν = 1$ $($binary $001)$ is followed by $κ = 4$ $($binary $100)$, | ||
| + | * $d(2)$ remains at the same position $2$ $($binary $010)$. | ||
| + | |||
| + | |||
| + | The actual FFT algorithm happens for the example $N = 8$ in $\log_2 N = 3$ stages, denoted $L = 1$, $L =2$ and $L = 3$. Further: | ||
| + | * In each stage, four basic operations - so-called '''butterflies''' - are to be performed. | ||
| + | * The values at the output of the first stage are designated in this task as $X(0),\hspace{0.03cm}\text{...} \hspace{0.1cm} , X(7)$, <br>those of the second as $Y(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , Y(7)$. | ||
| + | * After the third and last stage, all values must be divided by $N$. <br>The final result $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ is available here. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ''Hint:'' | ||
| + | *This task belongs to the chapter [[Signal_Representation/Fast_Fourier_Transform_(FFT)|Fast Fourier Transform (FFT)]]. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the DFT coefficient $D(\mu=3)$. |
|type="{}"} | |type="{}"} | ||
| − | $D(3) =$ { 0. } | + | $D(\mu=3) \ = \ $ { 0. } |
| − | { | + | {Calculate the DFT coefficient $D(\mu=4)$. |
|type="{}"} | |type="{}"} | ||
| − | $D(4) =$ { 1 3% } | + | $D(\mu=4) \ = \ $ { 1 3% } |
| − | { | + | {Determine the initial values $X(0)$, ... , $X(7)$ of the first stage. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - All $X$ values with even indices are equal to $2$. |
| − | + | + | + All $X$ values with odd indices are equal to $0$. |
| + | |||
| + | {Determine the initial values $Y(0)$, ... , $Y(7)$ of the second stage. Enter the values $Y(0)$ and $Y(4)$ as a check. | ||
| − | |||
|type="{}"} | |type="{}"} | ||
| − | $Y(0) =$ { 4 3% } | + | $Y(0) \ = \ $ { 4 3% } |
| − | $Y(4) =$ { -4.12--3.88 } | + | $Y(4) \ = \ $ { -4.12--3.88 } |
| − | { | + | {Calculate all $N$ spectral values $D(\mu)$, in particular |
|type="{}"} | |type="{}"} | ||
| − | $D(\mu = | + | $D(\mu =3) \ = \ $ { 0. } |
| − | $D(\mu | + | $D(\mu = 4) \ = \ $ { 1 3% } |
| − | { | + | {What would be the spectral coefficients for $d(ν = 4) = 1$ and $d(ν \neq 4) = 0$ ? <br>Enter the values $D(\mu =3)$ and $D(\mu =4)$ as a check. |
|type="{}"} | |type="{}"} | ||
| − | $D(\mu = 3) =$ { -1.03--0.97 } | + | $D(\mu = 3) \ = \ $ { -1.03--0.97 } |
| − | $D(\mu = 4) =$ { 1 3% } | + | $D(\mu = 4) \ = \ $ { 1 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' According to the general DFT equation given on the specification sheet, with $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot |
| + | \hspace{0.05cm}\pi /4}$ taking into account the alternating time coefficients: | ||
| − | $$ | + | :$$8 \cdot D(3) = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- |
| − | w^{21} | + | w^{21} = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- |
| − | w^{5}\hspace{0.05cm}. | + | w^{5}\hspace{0.05cm}.$$ |
| − | + | *Here it is taken into account that due to the periodicity $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist. | |
| + | *After re-sorting, the same applies: | ||
| − | $$ | + | :$$8 \cdot D(3) = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$ |
| − | |||
| − | + | *Thus, because $w_0 = 1$ and $w_4 = \text{e}^{-\text{j}\pi } = \hspace{0.08cm} - \hspace{-0.08cm}1$ , we obtain $\underline {D(\mu=3) = 0}$. | |
| − | '''2 | + | |
| + | '''(2)''' In analogy to sub-taske '''(1)''' , we now get: | ||
| − | $$ | + | :$$ 8 \cdot D(4) = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ |
| − | w^{24}- w^{28} | + | w^{24}- w^{28}= 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} |
| − | \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(4) = 1}\hspace{0.05cm}. | + | \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(\mu=4) = 1}\hspace{0.05cm}.$$ |
| − | |||
| − | '''3 | + | [[File:P_ID1178__Sig_A_5_5c_neu.png|right|frame|Example for the FFT algorithm]] |
| − | + | '''(3)''' <u>Proposed solution 2</u> is correct: | |
| + | *The term $w^0 = 1$ does not have to be taken into account. | ||
| + | *All output values with odd indices are zero by subtracting two identical input values. | ||
| + | *The first statement is not true: It holds $X(0) = X(2) = +2$ and $X(4) = X(6) = - 2$. | ||
| − | |||
| − | |||
| + | '''(4)''' The multiplication with $w^{2} = -{\rm j}$ can be dispensed with, since in the signal flow diagram the corresponding input values are zero. | ||
| + | *One thus obtains $Y(0) \;\underline{= 4}$ and $Y(4) \;\underline{= - \hspace{-0.03cm}4}$. | ||
| + | *All other values are zero. | ||
| − | '''5 | + | |
| + | |||
| + | '''(5)''' Because of $Y(5) = Y(6) =Y(7) = 0$, the multiplications with $w$, $w^2$ and $w^3$ do not matter in the third stage either. All spectral coefficients $D(\mu)$ therefore result in zero with the exception of | ||
| − | $$\hspace{0.15 cm}\underline{D(4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} | + | :$$\hspace{0.15 cm}\underline{D(\mu=4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} |
| + | \hspace{0.05cm},$$ | ||
| + | :$$\hspace{0.15 cm}\underline{D(\mu=3)} = D(\mu\ne 4) \hspace{0.15 cm}\underline{= 0} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | This result agrees with the results from '''(1)''' und '''(2)'''. | |
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Since both the time coefficients $d(ν)$ and all spectral coefficients $D(\mu)$ are purely real, there is no difference between the FFT and the IFFT. | ||
| + | *This means at the same time: The input and output values can be interchanged. | ||
| − | ''' | + | *Subtask '''(5)''' gave the following result: |
| − | |||
| − | $$d({\rm | + | :$$d({\rm even}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm |
| − | + | odd}\hspace{0.15cm}\nu)= -1$$ | |
| + | :$$\Rightarrow | ||
\hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$ | \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$ | ||
| − | + | *By swapping the input and output values, we arrive at problem '''(6)''': | |
| − | $$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} | + | :$$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} |
\Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, | \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, | ||
\hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 | \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *In particular, this results in $D(\mu=3) \; \underline{= -1}$ und $D(\mu=4) \; \underline{= +1}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.5 Fast Fourier Transform ^]] |
Latest revision as of 17:08, 21 May 2021
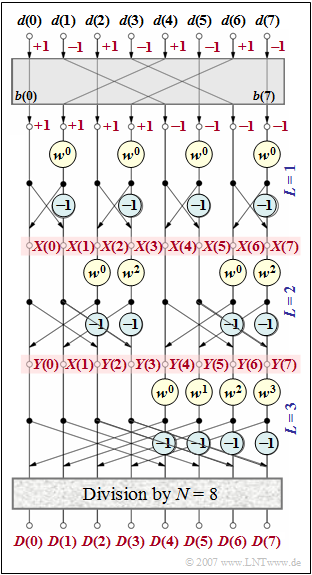
The graph shows the signal flow diagram of the Fast Fourier Transform $\rm (FFT)$ for $N = 8$.
The associated spectral coefficients $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ are determined from the time coefficients $d(0), \hspace{0.03cm}\text{...} \hspace{0.1cm}, d(7)$. The following applies to these with $0 ≤ μ ≤ 7$:
- $$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu}\hspace{0.05cm},$$
where the complex rotation factor $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}2\pi /N}$ is to be used, i.e. $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\pi /4}$ für $N = 8$.
- The alternating $±1$ sequence $\langle\hspace{0.05cm} d(ν)\hspace{0.05cm}\rangle$ is applied to the input.
- After the bit reversal operation, this results in the sequence $\langle \hspace{0.05cm}b(\kappa)\hspace{0.05cm}\rangle$.
It holds that $b(κ) = d(ν)$, if $ν$ is represented as a dual number and the resulting three bits are written as $κ$ in reverse order. For example
- $ν = 1$ $($binary $001)$ is followed by $κ = 4$ $($binary $100)$,
- $d(2)$ remains at the same position $2$ $($binary $010)$.
The actual FFT algorithm happens for the example $N = 8$ in $\log_2 N = 3$ stages, denoted $L = 1$, $L =2$ and $L = 3$. Further:
- In each stage, four basic operations - so-called butterflies - are to be performed.
- The values at the output of the first stage are designated in this task as $X(0),\hspace{0.03cm}\text{...} \hspace{0.1cm} , X(7)$,
those of the second as $Y(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , Y(7)$. - After the third and last stage, all values must be divided by $N$.
The final result $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ is available here.
Hint:
- This task belongs to the chapter Fast Fourier Transform (FFT).
Questions
Solution
- $$8 \cdot D(3) = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- w^{21} = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- w^{5}\hspace{0.05cm}.$$
- Here it is taken into account that due to the periodicity $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist.
- After re-sorting, the same applies:
- $$8 \cdot D(3) = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$
- Thus, because $w_0 = 1$ and $w_4 = \text{e}^{-\text{j}\pi } = \hspace{0.08cm} - \hspace{-0.08cm}1$ , we obtain $\underline {D(\mu=3) = 0}$.
(2) In analogy to sub-taske (1) , we now get:
- $$ 8 \cdot D(4) = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ w^{24}- w^{28}= 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(\mu=4) = 1}\hspace{0.05cm}.$$
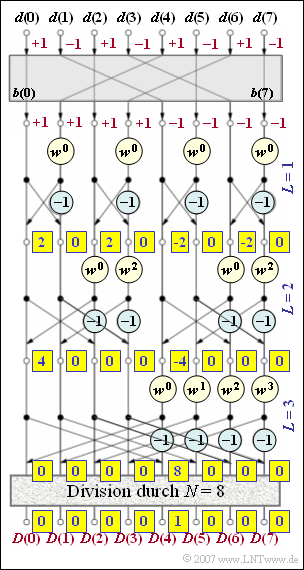
(3) Proposed solution 2 is correct:
- The term $w^0 = 1$ does not have to be taken into account.
- All output values with odd indices are zero by subtracting two identical input values.
- The first statement is not true: It holds $X(0) = X(2) = +2$ and $X(4) = X(6) = - 2$.
(4) The multiplication with $w^{2} = -{\rm j}$ can be dispensed with, since in the signal flow diagram the corresponding input values are zero.
- One thus obtains $Y(0) \;\underline{= 4}$ and $Y(4) \;\underline{= - \hspace{-0.03cm}4}$.
- All other values are zero.
(5) Because of $Y(5) = Y(6) =Y(7) = 0$, the multiplications with $w$, $w^2$ and $w^3$ do not matter in the third stage either. All spectral coefficients $D(\mu)$ therefore result in zero with the exception of
- $$\hspace{0.15 cm}\underline{D(\mu=4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} \hspace{0.05cm},$$
- $$\hspace{0.15 cm}\underline{D(\mu=3)} = D(\mu\ne 4) \hspace{0.15 cm}\underline{= 0} \hspace{0.05cm}.$$
This result agrees with the results from (1) und (2).
(6) Since both the time coefficients $d(ν)$ and all spectral coefficients $D(\mu)$ are purely real, there is no difference between the FFT and the IFFT.
- This means at the same time: The input and output values can be interchanged.
- Subtask (5) gave the following result:
- $$d({\rm even}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm odd}\hspace{0.15cm}\nu)= -1$$
- $$\Rightarrow \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$
- By swapping the input and output values, we arrive at problem (6):
- $$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 \hspace{0.05cm}.$$
- In particular, this results in $D(\mu=3) \; \underline{= -1}$ und $D(\mu=4) \; \underline{= +1}$.