Difference between revisions of "Aufgaben:Exercise 1.7Z: Overall Systems Analysis"
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
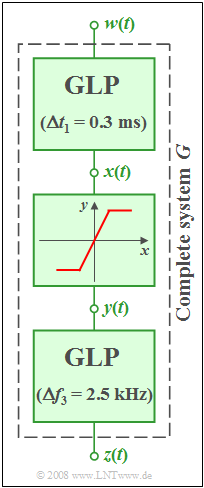
| − | [[File: | + | [[File:EN_LZI_Z_1_7.png|right|frame|System with Gaussian low-passe filters and non-linear characteristic curve]] |
| − | * | + | An overall system $G$ with input $w(t)$ and output $z(t)$ consists of three components: |
| − | :$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi(t/\Delta t_1)^2}, \hspace{0.5cm} \Delta | + | *The first component is a Gaussian low-pass filter with impulse response |
| + | :$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm} (t/\Delta t_1)^2}, \hspace{0.5cm} \Delta | ||
t_1= {0.3\,\rm ms}.$$ | t_1= {0.3\,\rm ms}.$$ | ||
| − | * | + | *This is then followed by a non-linearity with the characteristic curve |
| − | :$$y(t) = \left\{ \begin{array}{c} {8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge {4\,\rm V}}, \\ | + | :$$y(t) = \left\{ \begin{array}{c} +{8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge +{4\,\rm V}}, \\ |
| − | {{-4\,\rm V} < x(t) < {4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$ | + | {{-4\,\rm V} < x(t) < +{4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$ |
| − | :⇒ | + | :⇒ The input signal $x(t)$ of the non-linearity is amplified by the factor $2$ and – if necessary – limited to the range $±8 \ \rm V$ . |
| − | * | + | *At the end of the chain there is again a Gaussian low-pass filter given by its frequency response: |
| − | :$$H_3(f) = {\rm e}^{-\pi(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$ | + | :$$H_3(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$ |
| + | Let the input signal $w(t)$ of the overall system be a Gaussian pulse with amplitude $5 \ \rm V$ and variable (equivalent) duration $T$: | ||
| + | :$$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$ | ||
| + | What needs to be investigated is the range in which the equivalent impulse duration $T$ of this Gaussian pulse can vary such that the overall system can be entirely described by the frequency response | ||
| + | :$$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}.$$ | ||
| + | Here, the subscript "G" in frequency response and bandwidth stands for "Gesamtsystem" (German for "overall system"). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | ''Please note:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. | ||
| + | *In particular, reference is made to the page [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Gaussian_low-pass_filter|Gaussian low-pass filter]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What conditions must be satisfied for the overall system to be describable by a single frequency response? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + There is a linear relationship between $w(t)$ and $z(t)$. |
| − | - $H_3(f)$ | + | - $H_3(f)$ must be more narrow-band than $H_1(f)$. |
| − | + | + | + The signal $x(t)$ must not be greater in magnitude than $4 \ \rm V$. |
| − | { | + | {Compute the maximum value for the equivalent impulse duration $T$ so that the conditions given in '''(1)''' are satisfiable. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm max} \ =$ { 0.4 3% } $\ \rm ms$ | + | $T_{\rm max} \ = \ $ { 0.4 3% } $\ \rm ms$ |
| − | { | + | {Specify the parameters of the overall frequency response $H_{\rm G}(f)$ . |
|type="{}"} | |type="{}"} | ||
| − | $K \=$ { 2 3% } | + | $K \ = \ $ { 2 3% } |
| − | $\Delta f_{\rm G} =$ { 2 3% } $\ \rm kHz$ | + | $\Delta f_{\rm G} = \ $ { 2 3% } $\ \rm kHz$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Answers 1 and 3</u> are correct: | |
| + | *The first statement is correct: A frequency response can only be specified for a linear system. | ||
| + | *For this to be possible here, nonlinearity must not play a role. | ||
| + | *That is, it must be ensured that $|x(t)|$ is not greater than $4 \ \rm V$ . | ||
| + | *In contrast to this, the second statement is not true: The bandwidth of $H_3(f)$ does not affect whether the non-linearity can be eliminated or not. | ||
| − | |||
| − | + | '''(2)''' The first Gaussian low-pass filter is described in the frequency domain as follows: | |
| − | $$ | + | :$$X(f) = W(f) \cdot H_1(f) = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f \cdot T)^2} \cdot {\rm e}^{-\pi(f/\Delta f_1)^2} = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi f^2 (T^2 + \Delta t_1^2)}= {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f/\Delta f_x)^2}.$$ |
| − | + | *Here, $Δf_x$ denotes the equivalent bandwidth of $X(f)$. | |
| − | $$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$ | + | *The signal value at $t = 0$ is equal to the spectral area and at the same time to the maximum value of the signal: |
| − | : | + | *This should not exceed $4 \ \rm V$: |
| − | $$ | + | :$$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$ |
| − | \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16} | + | *From this it follows by comparison of coefficients: |
| − | + | :$$\frac{1}{T \cdot \Delta f_x} > \frac{5}{4}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} \frac{1}{T^2 \cdot \Delta f_x^2} > \frac{25}{16} | |
| + | \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16}$$ | ||
| + | :$$ \Rightarrow \hspace{0.1cm}\frac{ \Delta t_1^2}{T^2} > | ||
\frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ | \frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ | ||
\Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow | \Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow | ||
| − | \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}. | + | \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}.$$ |
| − | : | + | *The control calculation yields: |
| − | $$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = | + | :$$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = {1}/{\Delta t_x}= {2\,\rm kHz}$$ |
| − | $$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$ | + | :$$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$ |
| + | |||
| + | '''(3)''' The Gaussian low-pass filters satisfy the condition $H_1(f = 0) = H_3(f = 0) = 1$. | ||
| + | *Taking into account the gain of the second block in the linear domain the following is thus obtained for the total gain: | ||
| + | :$$\underline{K \ = \ 2}.$$ | ||
| − | + | *For the equivalent impulse duration of the overall system it holds that: | |
| − | + | :$$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm | |
| − | : | + | kHz}}\right)^2}={0.5\,\rm ms} \; \; \Rightarrow \; \; \Delta f_{\rm G} = {1}/{\Delta t_{\rm G}} \hspace{0.15cm}\underline{= {2\,\rm kHz}}.$$ |
| − | $$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm | ||
| − | kHz}}\right)^2}={0.5\,\rm ms} | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 82: | Line 96: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.3 Some Low-Pass Functions in Systems Theory^]] |
Latest revision as of 13:48, 8 September 2021
An overall system $G$ with input $w(t)$ and output $z(t)$ consists of three components:
- The first component is a Gaussian low-pass filter with impulse response
- $$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm} (t/\Delta t_1)^2}, \hspace{0.5cm} \Delta t_1= {0.3\,\rm ms}.$$
- This is then followed by a non-linearity with the characteristic curve
- $$y(t) = \left\{ \begin{array}{c} +{8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge +{4\,\rm V}}, \\ {{-4\,\rm V} < x(t) < +{4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$
- ⇒ The input signal $x(t)$ of the non-linearity is amplified by the factor $2$ and – if necessary – limited to the range $±8 \ \rm V$ .
- At the end of the chain there is again a Gaussian low-pass filter given by its frequency response:
- $$H_3(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$
Let the input signal $w(t)$ of the overall system be a Gaussian pulse with amplitude $5 \ \rm V$ and variable (equivalent) duration $T$:
- $$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$
What needs to be investigated is the range in which the equivalent impulse duration $T$ of this Gaussian pulse can vary such that the overall system can be entirely described by the frequency response
- $$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}.$$
Here, the subscript "G" in frequency response and bandwidth stands for "Gesamtsystem" (German for "overall system").
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Gaussian low-pass filter.
Questions
Solution
- The first statement is correct: A frequency response can only be specified for a linear system.
- For this to be possible here, nonlinearity must not play a role.
- That is, it must be ensured that $|x(t)|$ is not greater than $4 \ \rm V$ .
- In contrast to this, the second statement is not true: The bandwidth of $H_3(f)$ does not affect whether the non-linearity can be eliminated or not.
(2) The first Gaussian low-pass filter is described in the frequency domain as follows:
- $$X(f) = W(f) \cdot H_1(f) = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f \cdot T)^2} \cdot {\rm e}^{-\pi(f/\Delta f_1)^2} = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi f^2 (T^2 + \Delta t_1^2)}= {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f/\Delta f_x)^2}.$$
- Here, $Δf_x$ denotes the equivalent bandwidth of $X(f)$.
- The signal value at $t = 0$ is equal to the spectral area and at the same time to the maximum value of the signal:
- This should not exceed $4 \ \rm V$:
- $$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$
- From this it follows by comparison of coefficients:
- $$\frac{1}{T \cdot \Delta f_x} > \frac{5}{4}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} \frac{1}{T^2 \cdot \Delta f_x^2} > \frac{25}{16} \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16}$$
- $$ \Rightarrow \hspace{0.1cm}\frac{ \Delta t_1^2}{T^2} > \frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ \Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}.$$
- The control calculation yields:
- $$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = {1}/{\Delta t_x}= {2\,\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$
(3) The Gaussian low-pass filters satisfy the condition $H_1(f = 0) = H_3(f = 0) = 1$.
- Taking into account the gain of the second block in the linear domain the following is thus obtained for the total gain:
- $$\underline{K \ = \ 2}.$$
- For the equivalent impulse duration of the overall system it holds that:
- $$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm kHz}}\right)^2}={0.5\,\rm ms} \; \; \Rightarrow \; \; \Delta f_{\rm G} = {1}/{\Delta t_{\rm G}} \hspace{0.15cm}\underline{= {2\,\rm kHz}}.$$