Difference between revisions of "Aufgaben:Exercise 2.5Z: Compression Factor vs. Residual Redundancy"
From LNTwww
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Compression_According_to_Lempel,_Ziv_and_Welch |
}} | }} | ||
| − | [[File:P_ID2449__Inf_Z_2_5_neu.png|right|]] | + | [[File:P_ID2449__Inf_Z_2_5_neu.png|right|frame|Data length $L(N)$ after LZW coding for $\rm BQ1$ and $\rm BQ2$]] |
| − | : | + | As in [[Aufgaben:2.5_Restredundanz_bei_LZW-Codierung|Exercise 2.5]] we consider data compression using the [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#The_Lempel-Ziv-Welch_algorithm|Lempel–Ziv–Welch algorithm]]. Here holds: |
| + | * Let the input sequence have the length $N$. | ||
| + | * The length of the LZW coder output is $L$. | ||
| − | |||
| − | :* | + | The graph shows for two different binary sources $\rm BQ1$ and $\rm BQ2$ the relationship between the sequence lengths $N$ and $L$, represented by the function $L(N)$. |
| + | |||
| + | The two sources have the same statistical properties as in [[Aufgaben:Aufgabe_2.5:_Restredundanz_bei_LZW-Codierung|Exercise 2.5]]: | ||
| + | * $\rm BQ1$ is redundant due to unequal symbol probabilities $(p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11)$ . There are no dependencies between the individual symbols. The entropy is $H = 0.5$ bit/source symbol. | ||
| + | * $\rm BQ2$ is redundancy-free and thus has the entropy $H = 1$ bit/source symbol. | ||
| + | |||
| + | |||
| + | Furthermore, you need two definitions for the solution of this task: | ||
| + | *Let the "compression factor" be by definition | ||
| + | :$$K(N) = \frac{L(N)}{N}\hspace{0.05cm}.$$ | ||
| + | * The relative redundancy of the LZW code sequence (called "residual redundancy" in the following) is | ||
| + | :$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | + | Hints: |
| + | *The exercise belongs to the chapter [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch|Compression according to Lempel, Ziv and Welch]]. | ||
| + | *In particular, reference is made to the pages | ||
| + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Remaining_redundancy_as_a_measure_for_the_efficiency_of_coding_methods|Remainding redundancy as a measure of the efficiency of coding methods]], | ||
| + | :: [[Information_Theory/Compression_According_to_Lempel,_Ziv_and_Welch#Efficiency_of_Lempel-Ziv_coding|Efficiency of Lempel-Ziv coding]] and | ||
| + | :: [[Information_Theory/Compression_According_to_Lempel,_Ziv_and_Welch#Quantitative_statements_on_asymptotic_optimality|Quantitative statements on asymptotic optimality]]. | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which compression factors $K(N)$ result with $N = 10000$? |
|type="{}"} | |type="{}"} | ||
| − | $N = 10000 | + | $\rm BQ1$: $K(N = 10000) \ = \ $ { 0.68 3% } |
| − | $BQ2:\ | + | $\rm BQ2$: $K(N = 10000) \ = \ $ { 1.233 3% } |
| − | { | + | {What is the residual redundancy $r(N)$ (in percent)? Let $N = 10000$ apply again. |
|type="{}"} | |type="{}"} | ||
| − | $N = 10000 | + | $\rm BQ1$: $r(N = 10000) \ = \ $ { 26.5 3% } $\ \%$ |
| − | $BQ2:\ | + | $\rm BQ2$: $r(N = 10000) \ = \ $ { 19.0 3% } $\ \%$ |
| − | { | + | {What conclusions can be drawn from the comparison of $N = 10000$ and $N = 50000$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For both sources $K(N = 50000)$ is smaller than $K(N = 10000)$. |
| − | + | + | + For both sources $r(N = 50000)$ is smaller than $r(N = 10000)$. |
| − | - | + | - Only $\rm BQ1$ has more favourable values with $N = 50000$ . |
| Line 51: | Line 63: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The compression factor is defined as the quotient of the lengths of the LZW output sequence $(L)$ and input sequence $(N = 10000)$: | |
| − | :$${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm}, | + | :$${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm},$$ |
| − | + | :$$ {\rm BQ2:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{12330}{10000}\hspace{0.15cm}\underline{= 1.233}\hspace{0.05cm}. $$ | |
| − | + | *Of course, the LZW coding only makes sense with the redundant binary source $\rm BQ1$ . Here the amount of data can be reduced by $1-0.68=32\%$ . | |
| + | *With the redundancy-free binary source $\rm BQ2$ , on the other hand, the LZW coding leads to a $1.233-1=23.3\%$ larger data quantity. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | + | '''(2)''' From the given equation we obtain with $N = 10000$: |
| − | :$$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0. | + | :$${\rm BQ1:}\hspace{0.3cm} H = 0.5\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{0.5 \cdot N}{L } = 1 - \frac{5000}{6800 } \hspace{0.15cm}\underline{\approx 26.5\,\%}\hspace{0.05cm},$$ |
| + | :$$ {\rm BQ2:}\hspace{0.3cm} H = 1.0\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{N}{L } = 1 - \frac{10000}{12330 } \hspace{0.15cm}\underline{\approx 19\,\%}\hspace{0.05cm}.$$ | ||
| + | *The residual redundancy indicates the (relative) redundancy of the LZW output sequence. | ||
| + | *Although the source $\rm BQ1$ is more suitable for LZW coding than the redundancy-free source $\rm BQ2$, $\rm BQ1$ results in a larger residual redundancy because of the redundancy in the input sequence. | ||
| + | *A smaller residual redundancy $r(N)$ for a given $N$ therefore says nothing about whether LZW coding is useful for the source at hand. | ||
| + | *For this, the compression factor $K(N)$ must be considered. In general, the following relationship between $r(N)$ and $K(N)$ applies: | ||
| + | :$$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0.5cm} K(N) = H \cdot (1- r(N)) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | + | '''(3)''' From the table on the information page one can read (or deduce) | |
| − | :$$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0. | + | |
| − | + | *for the redundant binary source $\rm BQ1$: | |
| − | :$$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0. | + | :$$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 0.642\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 22.2\,\% \hspace{0.05cm}},$$ |
| − | + | *for the redundancy-free binary source $\rm BQ2$: | |
| + | :$$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 1.192\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 16.1\,\% \hspace{0.05cm}}.$$ | ||
| + | |||
| + | <u>Statements 1 and 2</u> are therefore correct: | ||
| + | * For both sources the compression factor $K(N)$ is smaller for $N = 50000$ than for $N = 10000$. | ||
| + | * The same applies to the residual redundancy: $r(N = 50000) < r(N = 10000)$. | ||
| + | * Both with regard to $K(N)$ and $r(N)$ "more favourable" values result with larger $N$ , even if, as with the redundancy-free binary source $\rm BQ2$, <br>the application of Lempel–Ziv actually leads to a deterioration. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 79: | Line 100: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^2.2 Lempel-Ziv-Welch Compression^]] |
Latest revision as of 13:13, 10 August 2021
As in Exercise 2.5 we consider data compression using the Lempel–Ziv–Welch algorithm. Here holds:
- Let the input sequence have the length $N$.
- The length of the LZW coder output is $L$.
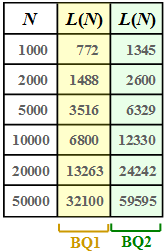
The graph shows for two different binary sources $\rm BQ1$ and $\rm BQ2$ the relationship between the sequence lengths $N$ and $L$, represented by the function $L(N)$.
The two sources have the same statistical properties as in Exercise 2.5:
- $\rm BQ1$ is redundant due to unequal symbol probabilities $(p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11)$ . There are no dependencies between the individual symbols. The entropy is $H = 0.5$ bit/source symbol.
- $\rm BQ2$ is redundancy-free and thus has the entropy $H = 1$ bit/source symbol.
Furthermore, you need two definitions for the solution of this task:
- Let the "compression factor" be by definition
- $$K(N) = \frac{L(N)}{N}\hspace{0.05cm}.$$
- The relative redundancy of the LZW code sequence (called "residual redundancy" in the following) is
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the pages
Questions
Solution
(1) The compression factor is defined as the quotient of the lengths of the LZW output sequence $(L)$ and input sequence $(N = 10000)$:
- $${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm},$$
- $$ {\rm BQ2:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{12330}{10000}\hspace{0.15cm}\underline{= 1.233}\hspace{0.05cm}. $$
- Of course, the LZW coding only makes sense with the redundant binary source $\rm BQ1$ . Here the amount of data can be reduced by $1-0.68=32\%$ .
- With the redundancy-free binary source $\rm BQ2$ , on the other hand, the LZW coding leads to a $1.233-1=23.3\%$ larger data quantity.
(2) From the given equation we obtain with $N = 10000$:
- $${\rm BQ1:}\hspace{0.3cm} H = 0.5\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{0.5 \cdot N}{L } = 1 - \frac{5000}{6800 } \hspace{0.15cm}\underline{\approx 26.5\,\%}\hspace{0.05cm},$$
- $$ {\rm BQ2:}\hspace{0.3cm} H = 1.0\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{N}{L } = 1 - \frac{10000}{12330 } \hspace{0.15cm}\underline{\approx 19\,\%}\hspace{0.05cm}.$$
- The residual redundancy indicates the (relative) redundancy of the LZW output sequence.
- Although the source $\rm BQ1$ is more suitable for LZW coding than the redundancy-free source $\rm BQ2$, $\rm BQ1$ results in a larger residual redundancy because of the redundancy in the input sequence.
- A smaller residual redundancy $r(N)$ for a given $N$ therefore says nothing about whether LZW coding is useful for the source at hand.
- For this, the compression factor $K(N)$ must be considered. In general, the following relationship between $r(N)$ and $K(N)$ applies:
- $$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0.5cm} K(N) = H \cdot (1- r(N)) \hspace{0.05cm}.$$
(3) From the table on the information page one can read (or deduce)
- for the redundant binary source $\rm BQ1$:
- $$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 0.642\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 22.2\,\% \hspace{0.05cm}},$$
- for the redundancy-free binary source $\rm BQ2$:
- $$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0.5cm} K(N = 50000) = 1.192\hspace{0.05cm},\hspace{0.5cm}r(N = 50000) \hspace{0.15cm}\underline {= 16.1\,\% \hspace{0.05cm}}.$$
Statements 1 and 2 are therefore correct:
- For both sources the compression factor $K(N)$ is smaller for $N = 50000$ than for $N = 10000$.
- The same applies to the residual redundancy: $r(N = 50000) < r(N = 10000)$.
- Both with regard to $K(N)$ and $r(N)$ "more favourable" values result with larger $N$ , even if, as with the redundancy-free binary source $\rm BQ2$,
the application of Lempel–Ziv actually leads to a deterioration.