Difference between revisions of "Aufgaben:Exercise 3.4: Entropy for Different PMF"
| (19 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables |
}} | }} | ||
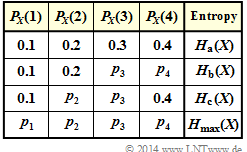
| − | [[File: | + | [[File:EN_Inf_Z_3_3.png|right|frame|Probability functions, each with $M = 4$ elements]] |
| − | In | + | In the first row of the adjacent table, the probability mass function denoted by $\rm (a)$ is given in the following. |
| − | |||
| − | |||
| − | + | For this PMF $P_X(X) = \big [0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ the entropy is to be calculated in subtask '''(1)''' : | |
| + | :$$H_{\rm a}(X) = {\rm E} \big [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\big ]= - {\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_{X}(X)}\big ].$$ | ||
| + | Since the logarithm to the base $2$ is used here, the pseudo-unit "bit" is to be added. | ||
| − | + | In the further tasks, some probabilities are to be varied in each case in such a way that the greatest possible entropy results: | |
| − | |||
| − | |||
| + | * By suitably varying $p_3$ and $p_4$, one arrives at the maximum entropy $H_{\rm b}(X)$ under the condition $p_1 = 0.1$ and $p_2 = 0.2$ ⇒ subtask '''(2)'''. | ||
| + | * By varying $p_2$ and $p_3$ appropriately, one arrives at the maximum entropy $H_{\rm c}(X)$ under the condition $p_1 = 0.1$ and $p_4 = 0.4$ ⇒ subtask '''(3)'''. | ||
| + | * In subtask '''(4)''' all four parameters are released for variation, which are to be determined according to the maximum entropy ⇒ $H_{\rm max}(X)$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Some preliminary remarks on two-dimensional random variables]]. | ||
| + | *In particular, reference is made to the page [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Probability_mass_function_and_entropy|Probability mass function and entropy]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {To which entropy does the probability mass function $P_X(X) = \big [ 0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ lead? |
|type="{}"} | |type="{}"} | ||
$H_{\rm a}(X) \ = \ $ { 1.846 0.5% } $\ \rm bit$ | $H_{\rm a}(X) \ = \ $ { 1.846 0.5% } $\ \rm bit$ | ||
| − | { | + | {Let $P_X(X) = \big [ 0.1, \ 0.2, \ p_3, \ p_4\big ]$ apply in general. What entropy is obtained if $p_3$ and $p_4$ are chosen as best as possible? |
|type="{}"} | |type="{}"} | ||
$H_{\rm b}(X) \ = \ $ { 1.857 0.5% } $\ \rm bit$ | $H_{\rm b}(X) \ = \ $ { 1.857 0.5% } $\ \rm bit$ | ||
| − | { | + | { Now let $P_X(X) = \big [ 0.1, \ p_2, \ p_3, \ 0.4 \big ]$. What entropy is obtained if $p_2$ and $p_3$ are chosen as best as possible? |
|type="{}"} | |type="{}"} | ||
$H_{\rm c}(X) \ = \ $ { 1.861 0.5% } $\ \rm bit$ | $H_{\rm c}(X) \ = \ $ { 1.861 0.5% } $\ \rm bit$ | ||
| − | { | + | { What entropy is obtained if all probabilities $(p_1, \ p_2 , \ p_3, \ p_4)$ can be chosen as best as possible? |
|type="{}"} | |type="{}"} | ||
$H_{\rm max}(X) \ = \ $ { 2 1% } $\ \rm bit$ | $H_{\rm max}(X) \ = \ $ { 2 1% } $\ \rm bit$ | ||
| Line 43: | Line 51: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' With $P_X(X) = \big [ 0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ we get for the entropy: |
| − | + | :$$H_{\rm a}(X) = | |
| − | $$H_{\rm a}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + | ||
0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + | 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}$$. | + | \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$ |
| + | Here (and in the other tasks) the pseudo-unit "bit" is to be added in each case. | ||
| − | |||
| − | |||
| − | $$H_{\rm b1}(X) = | + | '''(2)''' The entropy $H_{\rm b}(X)$ can be represented as the sum of two parts $H_{\rm b1}(X)$ and $H_{\rm b2}(X)$, with: |
| + | :$$H_{\rm b1}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
| − | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm}$$ | + | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$ |
| − | + | :$$H_{\rm b2}(X) = | |
| − | $$H_{\rm b2}(X) = | ||
p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + | p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + | ||
| − | (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}$$ | + | (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$ |
| − | + | *The second function is maximum for $p_3 = p_4 = 0.35$. A similar relationship has been found for the binary entropy function. | |
| + | *Thus one obtains: | ||
| − | $$H_{\rm b2}(X) = 2 \cdot | + | :$$H_{\rm b2}(X) = 2 \cdot |
p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = | p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = | ||
| − | 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060$$ | + | 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060 $$ |
| + | :$$ \Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$ | ||
| − | |||
| − | '''3 | + | '''(3)''' Analogous to subtask '''(2)''', $p_1 = 0.1$ and $p_4 = 0.4$ yield the maximum for $p_2 = p_3 = 0.25$: |
| − | + | :$$H_{\rm c}(X) = | |
| − | $$H_{\rm c}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + | 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}$$ | + | \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$ |
| − | |||
| − | $$H_{\rm max}(X) = | + | '''(4)''' The maximum entropy for the symbol range $M=4$ is obtained for equal probabilities, i.e. for $p_1 = p_2 = p_3 = p_4 = 0.25$: |
| + | :$$H_{\rm max}(X) = | ||
{\rm log}_2 \hspace{0.1cm} M | {\rm log}_2 \hspace{0.1cm} M | ||
| − | \hspace{0.15cm} \underline {= 2} \hspace{0.05cm} | + | \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | $$\Delta H(X) = 1- | + | *The difference of the entropies according to '''(4)''' and '''(3)''' gives ${\rm \Delta} H(X) = 0.139 \ \rm bit$. Here: |
| + | :$${\rm \Delta} H(X) = 1- | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.05cm}$$ | + | \hspace{0.05cm}.$$ |
| − | + | *With the binary entropy function | |
| − | $$H_{\rm bin}(p) = | + | :$$H_{\rm bin}(p) = |
p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + | p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + | ||
(1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$ | (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$ | ||
| − | + | :can also be written for this: | |
| − | $$\Delta H(X) = 0.5 \cdot \ | + | :$${\rm \Delta} H(X) = 0.5 \cdot \big [ 1- H_{\rm bin}(0.2) \big ] = |
| − | 0.5 \cdot \ | + | 0.5 \cdot \big [ 1- 0.722 \big ] = 0.139 |
| − | \hspace{0.05cm}$$ | + | \hspace{0.05cm}.$$ |
| Line 120: | Line 125: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.1 General Information on 2D Random Variables^]] |
Latest revision as of 09:13, 24 September 2021
In the first row of the adjacent table, the probability mass function denoted by $\rm (a)$ is given in the following.
For this PMF $P_X(X) = \big [0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ the entropy is to be calculated in subtask (1) :
- $$H_{\rm a}(X) = {\rm E} \big [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\big ]= - {\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_{X}(X)}\big ].$$
Since the logarithm to the base $2$ is used here, the pseudo-unit "bit" is to be added.
In the further tasks, some probabilities are to be varied in each case in such a way that the greatest possible entropy results:
- By suitably varying $p_3$ and $p_4$, one arrives at the maximum entropy $H_{\rm b}(X)$ under the condition $p_1 = 0.1$ and $p_2 = 0.2$ ⇒ subtask (2).
- By varying $p_2$ and $p_3$ appropriately, one arrives at the maximum entropy $H_{\rm c}(X)$ under the condition $p_1 = 0.1$ and $p_4 = 0.4$ ⇒ subtask (3).
- In subtask (4) all four parameters are released for variation, which are to be determined according to the maximum entropy ⇒ $H_{\rm max}(X)$ .
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- In particular, reference is made to the page Probability mass function and entropy.
Questions
Solution
- $$H_{\rm a}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$
Here (and in the other tasks) the pseudo-unit "bit" is to be added in each case.
(2) The entropy $H_{\rm b}(X)$ can be represented as the sum of two parts $H_{\rm b1}(X)$ and $H_{\rm b2}(X)$, with:
- $$H_{\rm b1}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$
- $$H_{\rm b2}(X) = p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$
- The second function is maximum for $p_3 = p_4 = 0.35$. A similar relationship has been found for the binary entropy function.
- Thus one obtains:
- $$H_{\rm b2}(X) = 2 \cdot p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060 $$
- $$ \Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$
(3) Analogous to subtask (2), $p_1 = 0.1$ and $p_4 = 0.4$ yield the maximum for $p_2 = p_3 = 0.25$:
- $$H_{\rm c}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$
(4) The maximum entropy for the symbol range $M=4$ is obtained for equal probabilities, i.e. for $p_1 = p_2 = p_3 = p_4 = 0.25$:
- $$H_{\rm max}(X) = {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$
- The difference of the entropies according to (4) and (3) gives ${\rm \Delta} H(X) = 0.139 \ \rm bit$. Here:
- $${\rm \Delta} H(X) = 1- 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.05cm}.$$
- With the binary entropy function
- $$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$
- can also be written for this:
- $${\rm \Delta} H(X) = 0.5 \cdot \big [ 1- H_{\rm bin}(0.2) \big ] = 0.5 \cdot \big [ 1- 0.722 \big ] = 0.139 \hspace{0.05cm}.$$