Difference between revisions of "Aufgaben:Exercise 2.4Z: Low-pass Influence with Synchronous Demodulation"
m (Guenter verschob die Seite 2.4Z Tiefpass-Einfluss bei SD nach 2.4Z Tiefpass-Einfluss bei Synchrondemodulation) |
m |
||
| (30 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1009__Mod_Z_2_4.png|right|frame| | + | [[File:P_ID1009__Mod_Z_2_4.png|right|frame|Signals for DSB–AM and synchronous demodulation]] |
| − | + | Let us consider the same communication system as in [[Aufgaben:Exercise_2.4:_Frequency_and_Phase_Offset|Exercise 2.4]]. But this time, we will assume perfect frequency and phase synchronization for the synchronous demodulator $\rm (SD)$ . | |
| − | |||
| − | $ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The source signal $q(t)$, the transmitted signal $s(t)$ and the signal $b(t)$ in the synchronous demodulator before the low-pass filter are given as follows: | |
| − | $$ | + | :$$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm with }$$ |
| + | ::$$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| + | ::$$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| + | :$$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| + | :$$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | ||
| + | The graph shows the source signal $q(t)$ at the top and the transmission signal $s(t)$ in the middle. | ||
| − | + | The sink signal $v(t)$ is shown at the bottom (purple waveform). | |
| − | + | *This obviously does not match the source signal (blue dashed curve). | |
| − | + | *The reason for this undesired result $v(t) ≠ q(t)$ could be a missing or wrongly dimensioned low-pass filter. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In the subtasks '''(3)''' and '''(4)''' , a [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Trapezoidal_low-pass_filters|"trapezoidal low-pass filter"]] is used, whose frequency response is as follows: | ||
| + | :$$H_{\rm E}(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$ | ||
| − | === | + | |
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Synchronous_Demodulation|Synchronous Demodulation]]. | ||
| + | *Particular reference is made to the page [[Modulation_Methods/Synchronous_Demodulation#Block_diagram_and_time_domain_representation|Block diagram and time domain representation]]. | ||
| + | *In contrast to [[Aufgaben:Exercise_2.4:_Frequency_and_Phase_Offset|Exercise 2.4]] , $f_1$ and $f_2$ do not describe signal frequencies, but instead relate to the low-pass filter. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements can be made about the $H_{\rm E}(f)$ filter used to obtain the sink signal shown on the page? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The upper cutoff frequency is too high. |
| − | - | + | - The upper cutoff frequency is too low. |
| − | - | + | - The lower cutoff frequency is not zero. |
| − | { | + | {With which of the low-pass functions listed below is ideal demodulation - that is, $v(t) = q(t)$ – possible in principle? |
| − | |type="[]"} | + | |type="[]"} |
| − | + | + | + Rectangular-in-frequency low-pass, |
| − | - | + | - Gaussian low-pass, |
| − | + | + | + trapezoidal low-pass, |
| − | - | + | - slit low-pass. |
| − | { | + | {What is the minimum lower corner frequency $f_1$ of a trapezoidal low-pass filter one can choose to avoid distortion? |
|type="{}"} | |type="{}"} | ||
| − | $f_{1, min}$ | + | $f_{\text{1, min}} \ = \ $ { 5 3% } $\ \text{kHz}$ |
| − | { | + | {What is the maximum upper corner frequency $f_2$ of the trapezoidal low-pass that avoids distortion? |
|type="{}"} | |type="{}"} | ||
| − | $f_{2,max}$ | + | $f_{\text{2, max}} \ = \ $ { 95 3% } $\ \text{kHz}$ |
| − | { | + | {Which cutoff frequency (German: "Grenzfrequenz" ⇒ subscript "G") $f_{\rm G}$ of an ideal rectangular low-pass filter would you choose if distortion is not negligible? |
| − | |type=" | + | |type="()"} |
| − | - $ | + | - $f_{\rm G} = 4 \ \rm kHz$, |
| − | + $ | + | + $f_{\rm G} = 6 \ \rm kHz$, |
| − | - $ | + | - $f_{\rm G} = 10 \ \rm kHz$. |
| Line 64: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>The first statement</u> is correct: |
| + | *The sink signal $v(t)$ shown in the bottom graphic exactly matches the signal $b(t)$ given in the equation and thus also contains components around twice the carrier frequency. | ||
| + | *The filter $H_{\rm E}(f)$ is either missing completely or its upper cutoff frequency $f_2$ is too high. | ||
| + | *Regarding the lower cutoff frequency $f_1$, the only statement possible is that it is smaller than the smallest frequency $\text{(2 kHz)}$ occurring in the signal $b(t)$. | ||
| + | *Whether or not a DC component is removed by the filter is unclear, since such a component is not present in the signal $b(t)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Answers 1 and 3</u> are correct: | ||
| + | *A prerequisite for distortion-free demodulation is that all spectral components up to a certain frequency $f_1$ are transmitted equally and as unattenuated as possible, and all components at frequencies $f > f_2$ are completely suppressed. | ||
| + | *The rectangular and trapezoidal low-pass filters satisfy this condition. | ||
| − | |||
| − | ''' | + | '''(3)''' It must be ensured that the $\text{5 kHz}$ component still lies in the passband: |
| + | :$$f_{\text{1, min}}\hspace{0.15cm}\underline{ =5 \ \rm kHz}.$$ | ||
| − | |||
| + | '''(4)''' All spectral components in the vicinity of twice the carrier frequency – more precisely between $\text{95 kHz}$ and $\text{ 105 kHz}$ – must be completely suppressed: | ||
| + | :$$f_{\text{2, max}}\hspace{0.15cm}\underline{ =95 \ \rm kHz}.$$ | ||
| + | *Otherwise nonlinear distortion would arise. | ||
| − | |||
| − | '''5 | + | '''(5)''' <u>Answer 2</u> is correct: |
| + | *The cutoff frequency} $f_{\rm G} = \text{ 4 kHz}$ would result in (linear) distortions, since the $\text{5 kHz}$ component would be cut off. | ||
| + | *The low-pass with cutoff frequency $f_{\rm G} = \text{6 kHz}$ is preferable, since with $f_{\rm G} = \text{10 kHz}$ more noise components would be superimposed on the signal $v(t)$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 86: | Line 104: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.2 Synchronous Demodulation^]] |
Latest revision as of 16:32, 25 March 2022
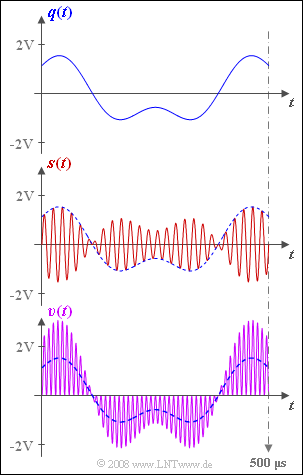
Let us consider the same communication system as in Exercise 2.4. But this time, we will assume perfect frequency and phase synchronization for the synchronous demodulator $\rm (SD)$ .
The source signal $q(t)$, the transmitted signal $s(t)$ and the signal $b(t)$ in the synchronous demodulator before the low-pass filter are given as follows:
- $$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm with }$$
- $$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- $$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- $$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- $$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
The graph shows the source signal $q(t)$ at the top and the transmission signal $s(t)$ in the middle.
The sink signal $v(t)$ is shown at the bottom (purple waveform).
- This obviously does not match the source signal (blue dashed curve).
- The reason for this undesired result $v(t) ≠ q(t)$ could be a missing or wrongly dimensioned low-pass filter.
In the subtasks (3) and (4) , a "trapezoidal low-pass filter" is used, whose frequency response is as follows:
- $$H_{\rm E}(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$
Hints:
- This exercise belongs to the chapter Synchronous Demodulation.
- Particular reference is made to the page Block diagram and time domain representation.
- In contrast to Exercise 2.4 , $f_1$ and $f_2$ do not describe signal frequencies, but instead relate to the low-pass filter.
Questions
Solution
- The sink signal $v(t)$ shown in the bottom graphic exactly matches the signal $b(t)$ given in the equation and thus also contains components around twice the carrier frequency.
- The filter $H_{\rm E}(f)$ is either missing completely or its upper cutoff frequency $f_2$ is too high.
- Regarding the lower cutoff frequency $f_1$, the only statement possible is that it is smaller than the smallest frequency $\text{(2 kHz)}$ occurring in the signal $b(t)$.
- Whether or not a DC component is removed by the filter is unclear, since such a component is not present in the signal $b(t)$.
(2) Answers 1 and 3 are correct:
- A prerequisite for distortion-free demodulation is that all spectral components up to a certain frequency $f_1$ are transmitted equally and as unattenuated as possible, and all components at frequencies $f > f_2$ are completely suppressed.
- The rectangular and trapezoidal low-pass filters satisfy this condition.
(3) It must be ensured that the $\text{5 kHz}$ component still lies in the passband:
- $$f_{\text{1, min}}\hspace{0.15cm}\underline{ =5 \ \rm kHz}.$$
(4) All spectral components in the vicinity of twice the carrier frequency – more precisely between $\text{95 kHz}$ and $\text{ 105 kHz}$ – must be completely suppressed:
- $$f_{\text{2, max}}\hspace{0.15cm}\underline{ =95 \ \rm kHz}.$$
- Otherwise nonlinear distortion would arise.
(5) Answer 2 is correct:
- The cutoff frequency} $f_{\rm G} = \text{ 4 kHz}$ would result in (linear) distortions, since the $\text{5 kHz}$ component would be cut off.
- The low-pass with cutoff frequency $f_{\rm G} = \text{6 kHz}$ is preferable, since with $f_{\rm G} = \text{10 kHz}$ more noise components would be superimposed on the signal $v(t)$.