Difference between revisions of "Aufgaben:Exercise 5.7Z: Application of the IDFT"
From LNTwww
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Implementation_of_OFDM_Systems |
}} | }} | ||
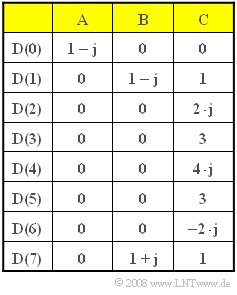
| − | [[File:P_ID1670__Mod_Z_5_7.png|right|frame| | + | [[File:P_ID1670__Mod_Z_5_7.png|right|frame|Three sets $\rm A$, $\rm B$ and $\rm C$ <br>for the spectral coefficients]] |
| − | + | In the [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|Discrete Fourier Transform]] $\rm (DFT)$, the discrete spectral coefficients $D(μ)$ with control variable $μ = 0$, ... , $N – 1$ are calculated from the time sample values $d(ν)$ with $ν = 0$, ... , $N – 1$ as follows: | |
| − | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0. | + | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ |
| − | + | Here, $w$ abbreviates the complex rotation factor: | |
:$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ | ||
| − | + | Correspondingly, for the [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Inverse_discrete_Fourier_transform|Inverse discrete Fourier transform]] $\rm (IDFT)$ practically as an "inverse function" of the DFT applies: | |
| − | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0. | + | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ |
| − | In | + | *In this exercise, the time coefficients $d(ν)$ are to be determined for different complex-valued example sequences $D(μ)$ – which are labeled $\rm A$, $\rm B$ and $\rm C$ in the table. |
| + | *Thus, $N = 8$ is always valid. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Modulation_Methods/Realisierung_von_OFDM-Systemen|Implementation of OFDM Systems]]. | ||
| + | *Reference is also made to the chapter [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|Discrete Fourier Transform]] in the book "Signal Representation". | ||
| + | *You can check your results with the interactive applet [[Applets:Discrete_Fouriertransform_and_Inverse|Discrete Fourier Transform and Inverse]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the time coefficients $d(ν)$ for the spectral coefficients $D(μ)$ according to $\rm A$? <br> Enter the first coefficient $d(1)$ with real and imaginary parts. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}[d(1)] \ = \ $ { 1 1% } | + | ${\rm Re}\big[d(1)\big] \ = \ $ { 1 1% } |
| − | ${\rm Im}[d(1)] \ = \ $ { -1.03--0.97 } | + | ${\rm Im}\big[d(1)\big] \ = \ $ { -1.03--0.97 } |
| − | { | + | {What are the time coefficients $d(ν)$ for the spectral coefficients $D(μ)$ according to $\rm B$? <br> Enter the first coefficient $d(1)$ with real and imaginary parts. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}[d(1)] \ = \ $ { 2.828 1% } | + | ${\rm Re}\big[d(1)\big] \ = \ $ { 2.828 1% } |
| − | ${\rm Im}[d(1)] \ = \ $ { 0. } | + | ${\rm Im}\big[d(1)\big] \ = \ $ { 0. } |
| − | { | + | {What are the time coefficients $d(ν)$ for the spectral coefficients $D(μ)$ according to $\rm C$? <br> Enter the first coefficient $d(1)$ with real and imaginary parts. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}[d(1)] \ = \ $ { -6.9--6.7 } | + | ${\rm Re}\big[d(1)\big] \ = \ $ { -6.9--6.7 } |
| − | ${\rm Im}[d(1)] \ = \ ${ -4.04--3.96 } | + | ${\rm Im}\big[d(1)\big] \ = \ ${ -4.04--3.96 } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Because of $D(μ) = 0$ for $μ ≠ 0$ all time coefficients $d(ν) = D(0)= 1 - {\rm j}$. Thus: |
:$${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$ | :$${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Here, all spectral coefficients are zero except $D_1 = 1 - {\rm j}$ and $D_7 = 1 + {\rm j}$. It follows for all time coefficients $(0 ≤ ν ≤ 7)$: |
:$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ | :$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ | ||
| − | + | *However, due to periodicity, also holds: | |
:$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}= | :$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}= | ||
\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$ | \left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$ | ||
| − | + | *Using Euler's theorem, this expression can be transformed as follows: | |
:$$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$ | :$$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$ | ||
| − | + | *This time function $d(ν)$ is purely real and characterizes a harmonic oscillation with amplitude $ 2 \cdot \sqrt{2}$ and phase $φ = 45^\circ$. | |
| + | *The time coefficient with index $ν = 1$ indicates the maximum: | ||
:$$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$ | :$$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$ | ||
| − | '''(3)''' | + | |
| − | $$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} = | + | '''(3)''' According to the general equation: |
| − | + | :$$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} = \left[ D(1) + D(7) \right]\cdot \cos \left( {\pi}/{4} \right) + \left[ D(3) + D(5) \right]\cdot \cos \left( {3\pi}/{4} \right)+ | |
| − | + | {\rm j} \cdot \left[ D(2) - D(6) \right]\cdot \sin \left( {\pi}/{2} \right) + D(4) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}}.$$ | |
| − | + | *The first three terms give pure real results: | |
| − | $${\rm Re} | + | :$${\rm Re}[d(1)] = (1+1) \cdot \frac{1}{\sqrt{2}}-(3+3) \cdot \frac{1}{\sqrt{2}}+ {\rm j} \cdot4{\rm j} \cdot 1 = -\frac{4}{\sqrt{2}}-4\hspace{0.15cm}\underline { \approx -6.829}.$$ |
| − | + | *For the imaginary part, we obtain: | |
| − | + | :$${\rm Im}[d(1)] = {\rm Im}\left[4 \cdot{\rm j} \cdot (-1) \right] \hspace{0.15cm}\underline {= -4}.$$ | |
| − | $${\rm Im} | ||
| Line 72: | Line 77: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.6 Realization of OFDM Systems^]] |
Latest revision as of 09:35, 12 January 2022
In the Discrete Fourier Transform $\rm (DFT)$, the discrete spectral coefficients $D(μ)$ with control variable $μ = 0$, ... , $N – 1$ are calculated from the time sample values $d(ν)$ with $ν = 0$, ... , $N – 1$ as follows:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Here, $w$ abbreviates the complex rotation factor:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
Correspondingly, for the Inverse discrete Fourier transform $\rm (IDFT)$ practically as an "inverse function" of the DFT applies:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
- In this exercise, the time coefficients $d(ν)$ are to be determined for different complex-valued example sequences $D(μ)$ – which are labeled $\rm A$, $\rm B$ and $\rm C$ in the table.
- Thus, $N = 8$ is always valid.
Notes:
- The exercise belongs to the chapter Implementation of OFDM Systems.
- Reference is also made to the chapter Discrete Fourier Transform in the book "Signal Representation".
- You can check your results with the interactive applet Discrete Fourier Transform and Inverse.
Questions
Solution
(1) Because of $D(μ) = 0$ for $μ ≠ 0$ all time coefficients $d(ν) = D(0)= 1 - {\rm j}$. Thus:
- $${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$
(2) Here, all spectral coefficients are zero except $D_1 = 1 - {\rm j}$ and $D_7 = 1 + {\rm j}$. It follows for all time coefficients $(0 ≤ ν ≤ 7)$:
- $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$
- However, due to periodicity, also holds:
- $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}= \left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$
- Using Euler's theorem, this expression can be transformed as follows:
- $$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$
- This time function $d(ν)$ is purely real and characterizes a harmonic oscillation with amplitude $ 2 \cdot \sqrt{2}$ and phase $φ = 45^\circ$.
- The time coefficient with index $ν = 1$ indicates the maximum:
- $$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$
(3) According to the general equation:
- $$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} = \left[ D(1) + D(7) \right]\cdot \cos \left( {\pi}/{4} \right) + \left[ D(3) + D(5) \right]\cdot \cos \left( {3\pi}/{4} \right)+ {\rm j} \cdot \left[ D(2) - D(6) \right]\cdot \sin \left( {\pi}/{2} \right) + D(4) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}}.$$
- The first three terms give pure real results:
- $${\rm Re}[d(1)] = (1+1) \cdot \frac{1}{\sqrt{2}}-(3+3) \cdot \frac{1}{\sqrt{2}}+ {\rm j} \cdot4{\rm j} \cdot 1 = -\frac{4}{\sqrt{2}}-4\hspace{0.15cm}\underline { \approx -6.829}.$$
- For the imaginary part, we obtain:
- $${\rm Im}[d(1)] = {\rm Im}\left[4 \cdot{\rm j} \cdot (-1) \right] \hspace{0.15cm}\underline {= -4}.$$