Difference between revisions of "Aufgaben:Exercise 1.5: Cosine-Square Spectrum"
| (17 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Properties_of_Nyquist_Systems |
}} | }} | ||
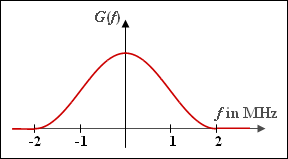
| − | [[File:P_ID1282__Dig_A_1_5.png|right|frame| | + | [[File:P_ID1282__Dig_A_1_5.png|right|frame|Cosine-square Nyquist spectrum]] |
| − | + | The spectrum $G(f)$ with $\cos^{2}$–shaped course is considered according to the sketch. This satisfies the first Nyquist criterion: | |
| − | :$$\sum_{k = -\infty}^{+\infty} G(f - | + | :$$\sum_{k = -\infty}^{+\infty} G(f -{k}/{T} ) = {\rm const.}$$ |
| − | + | Accordingly, the associated pulse $g(t)$ has zero crossings at multiples of $T$, where $T$ remains to be determined. The inverse Fourier transform of $G(f)$ yields the equation for the time course: | |
| − | |||
:$$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot | :$$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot | ||
| − | t/T)^2}\cdot {\rm | + | t/T)^2}\cdot {\rm sinc}( {t}/{T})\hspace{0.5cm} \text{with}\hspace{0.5cm} {\rm sinc}(x)=\sin(\pi x)/(\pi x)\hspace{0.05cm}.$$ |
| − | + | The questions for this exercise refer to the following properties: | |
| − | * | + | *The spectral function $G(f)$ is a special case of the cosine rolloff spectrum, which is point symmetric about the Nyquist frequency $f_{\rm Nyq}$. |
| − | * | + | *The cosine rolloff spectrum is completely characterized by the corner frequencies $f_{1}$ and $f_{2}$. |
| − | * | + | * For $| f | < f_{1}$, $G(f) = g_{0} \cdot T = \rm const.$, while the spectrum for $| f | > f_{2}$ has no components. |
| + | *The relation between the Nyquist frequency and the corner frequencies is: | ||
:$$f_{\rm Nyq}= \frac{f_1 +f_2 } | :$$f_{\rm Nyq}= \frac{f_1 +f_2 } | ||
{2 }\hspace{0.05cm}.$$ | {2 }\hspace{0.05cm}.$$ | ||
| − | * | + | *The edge steepness is characterized by the so-called rolloff factor: |
:$$r = \frac{f_2 -f_1 } | :$$r = \frac{f_2 -f_1 } | ||
{f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$ | {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | === | + | Note: The exercise belongs to the chapter [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems|"Properties of Nyquist Systems"]]. |
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {What are the corner frequencies of this cosine rolloff spectrum? | ||
| + | |type="{}"} | ||
| + | $f_{1} \ = \ $ { 0 3% } $\ \rm MHz$ | ||
| + | $f_{2} \ = \ $ { 2 3% } $\ \rm MHz$ | ||
| + | |||
| + | {What are the Nyquist frequency and the rolloff factor? | ||
| + | |type="{}"} | ||
| + | $f_{\rm Nyq} \ = \ $ { 1 3% } $\ \rm MHz$ | ||
| + | $r \ = \ $ { 1 3% } | ||
| + | |||
| + | {At what time interval $T$ does $g(t)$ have zero crossings? | ||
| + | |type="{}"} | ||
| + | $T \ = \ $ { 0.5 3% } $\ \rm µ s$ | ||
| + | |||
| + | {Which of the following statements is true? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | + $g(t)$ satisfies the first Nyquist criterion because of the $\rm sinc$–term. |
| − | + | + | - $g(t)$ has further zero crossings at $\pm 0.5T, \pm 1.5T, \pm 2.5 T, \text{...}$ |
| + | + The $\cos^{2}$–spectrum also satisfies the second Nyquist criterion. | ||
| − | { | + | {What is the (normalized) value of the pulse at time $t = T/2$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $g(t = T/2)/g_{0} \ = \ $ { 0.5 3% } |
| Line 42: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The upper corner frequency can be read from the diagram: $f_{2} \underline{= 2 \ \rm MHz}$. Since the spectrum is not constant in any range, $f_{1} \underline {= 0}$. |
| − | '''(2)''' | + | |
| − | '''(3)''' | + | |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | '''(2)''' From the given equations we obtain: |
| − | + | :$$f_{\rm Nyq} = \ \frac{f_1 +f_2 } | |
| + | {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' The spacing of equidistant zero crossings is directly related to the Nyquist frequency: | ||
| + | :$$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' <u>Statements 1 and 3</u> are correct: | ||
| + | *The first statement is correct: The function ${\rm sinc}(t/T)$ leads to zero crossings at $\nu T (\nu \neq 0)$. | ||
| + | *The last statement is also true: Because of $g(t) = 0$ for $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ the second Nyquist criterion is also fulfilled. | ||
| + | *On the other hand, the middle statement is false, since $g(t = T/2) \neq 0$. | ||
| + | *The condition for the second Nyquist criterion is in the frequency domain: | ||
| + | :$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - | ||
| + | {k}/{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= | ||
| + | {\rm const.}$$ | ||
| + | *The condition is indeed fulfilled for the cos$^{2}$–spectrum, as can be shown after a longer calculation. | ||
| + | *We restrict ourselves here to the frequency range $| f · T | \leq 1$ and set $g_{0} \cdot T = 1$ for simplicity: | ||
| + | :$$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | ||
| + | - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) | ||
| + | \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | ||
| + | + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) | ||
| + | \cdot T \right ]}\hspace{0.05cm}.$$ | ||
| + | *Further holds: | ||
| + | :$$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac | ||
| + | {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac | ||
| + | {1}{\cos(2x)}\right ]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} | ||
| + | \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | ||
| + | - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | ||
| + | + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$ | ||
| + | * Because of $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos | ||
| + | \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm | ||
| + | \pi f T \right)\text{:}$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin | ||
| + | (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' For $t = T/2$, the given equation yields an indeterminate value ("0 divided by 0"), which can be determined using l'Hospital's rule. | ||
| + | *To do this, form the derivatives of the numerator and denominator and insert the desired time $t = T/2$ into the result: | ||
| + | |||
| + | :$$\frac{g( t = T/2)}{g_0} = \ {{\rm sinc}( \frac{t}{T}) | ||
| + | \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot | ||
| + | t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} | ||
| + | \bigg |_{t = T/2} = \ {{\rm sinc}( \frac{t}{T}) \cdot \frac{- \pi/T \cdot | ||
| + | \sin(\pi \cdot t/T)}{-2 \cdot (2\cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot | ||
| + | \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$ | ||
| + | *A second solution method leads to the expression: | ||
| + | :$$\frac{g( t )}{g_0} = {\rm sinc}( \frac{t}{T}) \cdot | ||
| + | \frac {\pi}{4} \cdot \big [ {\rm sinc}( t/T + 1/2) + | ||
| + | {\rm sinc}(t/T - 1/2)\big] \hspace{0.05cm}.$$ | ||
| + | *The second bracket expression can be transformed as follows: | ||
| + | :$$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} | ||
| + | \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi | ||
| + | \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi | ||
| + | \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = \ \frac {1}{2} \cdot {\rm cos}(\pi | ||
| + | \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 | ||
| + | \cdot t/T - 1}\right] $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} | ||
| + | \bigg ] = \ \frac {1}{2} \cdot {\rm cos}(\pi | ||
| + | \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 | ||
| + | \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 | ||
| + | \cdot t/T)^2}\hspace{0.05cm}.$$ | ||
| + | *It follows that both expressions are actually equal. Thus, for time $t = T/2$, the following is still true: | ||
| + | :$$\frac{g( t = T/2)}{g_0} = {\rm sinc}( 0.5) \cdot \frac | ||
| + | {\pi}{4} \cdot \big [ {\rm sinc}(1 ) + {\rm sinc}(0)\big]= \frac | ||
| + | {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.3 Nyquist System Properties^]] |
Latest revision as of 13:24, 2 May 2022
The spectrum $G(f)$ with $\cos^{2}$–shaped course is considered according to the sketch. This satisfies the first Nyquist criterion:
- $$\sum_{k = -\infty}^{+\infty} G(f -{k}/{T} ) = {\rm const.}$$
Accordingly, the associated pulse $g(t)$ has zero crossings at multiples of $T$, where $T$ remains to be determined. The inverse Fourier transform of $G(f)$ yields the equation for the time course:
- $$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\cdot {\rm sinc}( {t}/{T})\hspace{0.5cm} \text{with}\hspace{0.5cm} {\rm sinc}(x)=\sin(\pi x)/(\pi x)\hspace{0.05cm}.$$
The questions for this exercise refer to the following properties:
- The spectral function $G(f)$ is a special case of the cosine rolloff spectrum, which is point symmetric about the Nyquist frequency $f_{\rm Nyq}$.
- The cosine rolloff spectrum is completely characterized by the corner frequencies $f_{1}$ and $f_{2}$.
- For $| f | < f_{1}$, $G(f) = g_{0} \cdot T = \rm const.$, while the spectrum for $| f | > f_{2}$ has no components.
- The relation between the Nyquist frequency and the corner frequencies is:
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- The edge steepness is characterized by the so-called rolloff factor:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$
Note: The exercise belongs to the chapter "Properties of Nyquist Systems".
Questions
Solution
(2) From the given equations we obtain:
- $$f_{\rm Nyq} = \ \frac{f_1 +f_2 } {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$
(3) The spacing of equidistant zero crossings is directly related to the Nyquist frequency:
- $$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$
(4) Statements 1 and 3 are correct:
- The first statement is correct: The function ${\rm sinc}(t/T)$ leads to zero crossings at $\nu T (\nu \neq 0)$.
- The last statement is also true: Because of $g(t) = 0$ for $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ the second Nyquist criterion is also fulfilled.
- On the other hand, the middle statement is false, since $g(t = T/2) \neq 0$.
- The condition for the second Nyquist criterion is in the frequency domain:
- $$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - {k}/{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$
- The condition is indeed fulfilled for the cos$^{2}$–spectrum, as can be shown after a longer calculation.
- We restrict ourselves here to the frequency range $| f · T | \leq 1$ and set $g_{0} \cdot T = 1$ for simplicity:
- $$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\hspace{0.05cm}.$$
- Further holds:
- $$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac {1}{\cos(2x)}\right ]$$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$
- Because of $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm \pi f T \right)\text{:}$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$
(5) For $t = T/2$, the given equation yields an indeterminate value ("0 divided by 0"), which can be determined using l'Hospital's rule.
- To do this, form the derivatives of the numerator and denominator and insert the desired time $t = T/2$ into the result:
- $$\frac{g( t = T/2)}{g_0} = \ {{\rm sinc}( \frac{t}{T}) \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} \bigg |_{t = T/2} = \ {{\rm sinc}( \frac{t}{T}) \cdot \frac{- \pi/T \cdot \sin(\pi \cdot t/T)}{-2 \cdot (2\cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$
- A second solution method leads to the expression:
- $$\frac{g( t )}{g_0} = {\rm sinc}( \frac{t}{T}) \cdot \frac {\pi}{4} \cdot \big [ {\rm sinc}( t/T + 1/2) + {\rm sinc}(t/T - 1/2)\big] \hspace{0.05cm}.$$
- The second bracket expression can be transformed as follows:
- $$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 \cdot t/T - 1}\right] $$
- $$\Rightarrow \hspace{0.3cm} \frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$
- It follows that both expressions are actually equal. Thus, for time $t = T/2$, the following is still true:
- $$\frac{g( t = T/2)}{g_0} = {\rm sinc}( 0.5) \cdot \frac {\pi}{4} \cdot \big [ {\rm sinc}(1 ) + {\rm sinc}(0)\big]= \frac {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$