Difference between revisions of "Aufgaben:Exercise 1.4: Nyquist Criteria"
| (16 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Properties_of_Nyquist_Systems |
}} | }} | ||
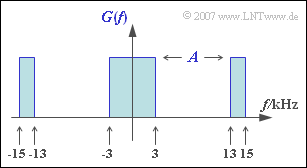
| − | [[File:P_ID1278__Dig_A_1_4.png|right|frame| | + | [[File:P_ID1278__Dig_A_1_4.png|right|frame|Rectangular Nyquist spectrum]] |
| − | + | Given by the sketch is the spectrum $G(f)$ of the basic detection pulse, where the parameter $A$ is still to be determined. Among other things it is to be checked whether this basic detection pulse fulfills one of the two Nyquist criteria. These are: | |
| − | * | + | *The '''first Nyquist criterion''' is fulfilled if for the spectral function holds: |
:$$\sum_{k = -\infty}^{+\infty} G(f - | :$$\sum_{k = -\infty}^{+\infty} G(f - | ||
{k}/{T} ) = {\rm const.}$$ | {k}/{T} ) = {\rm const.}$$ | ||
| − | :In | + | :In this case, the pulse $g(t)$ has zero crossings at $t = ν \cdot T$ for all integer values of $ν$ except $ν = 0$. For the entire exercise, $T = 0.1 \, \rm ms$ is assumed. |
| − | * | + | *If the '''second Nyquist criterion''' is satisfied, $g(t)$ has zero crossings at $\pm 1.5 T$, $\pm 2.5 T$, etc. |
| − | + | ||
| − | * | + | |
| − | + | ||
| − | * | + | Notes: |
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems|"Properties of Nyquist Systems"]]. | ||
| + | |||
| + | *The two equations are assumed to be known: | ||
:$$X(f) = \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad | :$$X(f) = \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}}\hspace{0.15cm}|f| < f_0 \hspace{0.05cm}, |
| − | \\ {\rm{ | + | \\ {\rm{for}}\hspace{0.15cm}|f| > f_0 \hspace{0.08cm} \\ |
\end{array} \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} x(t) | \end{array} \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} x(t) | ||
| − | =2 \cdot A \cdot f_0 \cdot {\rm si}(2 \pi | + | =2 \cdot A \cdot f_0 \cdot {\rm si}(2 \pi f_0 T) \hspace{0.05cm},\hspace{0.4cm} {\rm si} (x) = \sin(x)/x\hspace{0.05cm},$$ |
| − | :$$\sin(\alpha) \cdot \cos (\beta) = \frac{1}{2} \cdot \ | + | :$$\sin(\alpha) \cdot \cos (\beta) = \frac{1}{2} \cdot \big[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\big] |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Does the given pulse $g(t)$ satisfy the first Nyquist criterion? |
| − | |type=" | + | |type="()"} |
| − | + | + | +The first Nyquist criterion is fulfilled. |
| − | - | + | -The first Nyquist criterion is not fulfilled. |
| − | { | + | {Determine the parameter $A$ such that $g(t = 0) = 2\, \rm V$ holds. |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 0.2 3% } $ \ \rm mV/Hz$ | $A \ = \ $ { 0.2 3% } $ \ \rm mV/Hz$ | ||
| − | { | + | {Calculate $g(t)$ from $G(f)$ by applying the inverse Fourier transform. What (normalized) function value is obtained at $t = T$? |
|type="{}"} | |type="{}"} | ||
$ g(t = T)/g(t = 0) \ = \ $ { 0. } | $ g(t = T)/g(t = 0) \ = \ $ { 0. } | ||
| − | { | + | {Which (normalized) value results for $t = 2.5T$? |
|type="{}"} | |type="{}"} | ||
$g(t = 2.5 T)/g(t = 0)\ = \ $ { -0.39346--0.37054 } | $g(t = 2.5 T)/g(t = 0)\ = \ $ { -0.39346--0.37054 } | ||
| − | { | + | {Does the pulse $g(t)$ satisfy the second Nyquist criterion? |
| − | |type=" | + | |type="()"} |
| − | - | + | -The second Nyquist criterion is fulfilled. |
| − | + | + | +The second Nyquist criterion is not fulfilled. |
| Line 57: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
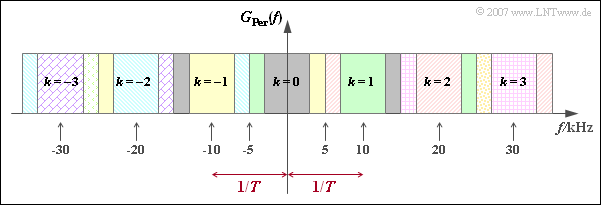
| − | '''(1)''' | + | '''(1)''' The following diagram shows the spectrum (the index "Per" here stands for "Periodic Continuation"): |
| + | [[File:P_ID1280__Dig_A_1_4a.png|right|frame|Illustration of the first Nyquist criterion]] | ||
| + | |||
:$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - | :$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - | ||
\frac{k}{T} ) \hspace{0.05cm}.$$ | \frac{k}{T} ) \hspace{0.05cm}.$$ | ||
| − | + | *The indexing variable $k = 0$ indicates the original spectral function $G(f)$. This is filled in gray. | |
| − | + | *The spectrum shifted to the right by the value $1/T = 10\, \rm kHz$ belongs to $k = 1$ and is marked in green, while $k = -1$ leads to the function highlighted in yellow. | |
| − | + | *The red and blue areas mark the contributions of the indexing variables $k = 2$ and $k = - 2$. | |
| − | + | ||
| + | |||
| + | It can be seen that $G_{\rm Per}(f)$ is constant. From this it follows that the first Nyquist criterion is fulfilled ⇒ <u>solution 1</u> is correct. | ||
| + | |||
| − | '''(2)''' | + | '''(2)''' Due to the Fourier integrals the following relation holds: |
:$$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f | :$$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f | ||
= A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz}$$ | = A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz}$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 2 | + | :$$\Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 0.2 \, {\rm mV/Hz}} \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | '''(3)''' Let $g(t) = g_{1}(t) +g_{2}(t)$, where | ||
| + | *$g_{1}(t)$ contains the spectral components in the interval $\pm 3 \, \rm kHz$ and | ||
| + | *$g_{2}(t)$ those between $13 \, \rm kHz$ and $15 \, \rm kHz$ (and between $-13 \, \rm kHz$ and $-15 \, \rm kHz$). | ||
| − | + | With the Fourier correspondence given, the two components are: | |
| − | |||
:$$g_1(t) \ = \ A \cdot 6\,{\rm kHz} \cdot {\rm si}(\pi \cdot 6\,{\rm kHz} \cdot t) | :$$g_1(t) \ = \ A \cdot 6\,{\rm kHz} \cdot {\rm si}(\pi \cdot 6\,{\rm kHz} \cdot t) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 81: | Line 93: | ||
\cdot 2 \cdot {\rm cos}(2 \pi \cdot 14\,{\rm kHz} \cdot t) | \cdot 2 \cdot {\rm cos}(2 \pi \cdot 14\,{\rm kHz} \cdot t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The second equation follows from the relation: | |
:$$G_2(f) = \left[ \delta(f + 14\,{\rm kHz}) + \delta(f - 14\,{\rm kHz})\right] \star \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad | :$$G_2(f) = \left[ \delta(f + 14\,{\rm kHz}) + \delta(f - 14\,{\rm kHz})\right] \star \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}}\hspace{0.15cm}|f| < 1\,{\rm kHz} \hspace{0.05cm}, |
| − | \\ {\rm{ | + | \\ {\rm{for}}\hspace{0.15cm}|f| > 1\,{\rm kHz} \hspace{0.05cm}. \\ |
\end{array}$$ | \end{array}$$ | ||
| − | + | The bottom diagram shows the numerically determined time history $g(t)$. For the time $t = T = 0.1\, \rm ms$ (yellow square) we get: | |
| − | :$$g_2(t = T ) | + | :$$g_2(t = T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.2 \cdot \pi)\cdot \cos (2.8 \cdot \pi) |
| − | + | = \frac{ A \cdot 4\,{\rm kHz}}{0.2 \cdot \pi}\cdot {\rm sin}(0.2 \cdot \pi | |
| − | + | )\cdot\cos (0.8 \cdot \pi) = \frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot [{\rm sin}(-0.6 \cdot | |
| − | )\cdot\cos (0.8 \cdot \pi) = | + | \pi)+ {\rm sin}(\pi)] $$ |
| − | + | [[File:EN_Dig_A_1_4.png|right|frame|Higher frequency Nyquist pulse]] | |
| − | \pi)+ {\rm sin}(\pi)] = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot | + | :$$\Rightarrow \hspace{0.3cm} g_2(t = T ) = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot |
| − | \pi)$$ | + | \pi).$$ |
| − | :$$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm | + | |
| − | + | For the first component $g_1(t)$, at time $t = T$: | |
| − | )= - g_2(t = T )$$ | + | :$$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm sinc}(0.6 |
| + | )$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}g_1(t = T ) = \frac{ A \cdot 6\,{\rm kHz}}{0.6 \cdot \pi}\cdot {\rm sin}(0.6 \cdot \pi | ||
| + | )$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}g_1(t = T ) = - g_2(t = T )$$ | ||
:$$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$ | ||
| − | + | This result is not surprising because of the Nyquist property. | |
| − | + | <br clear=all> | |
| − | + | '''(4)''' For $t = 2.5 T$ (green square), the following partial results are obtained: | |
| − | '''(4)''' | ||
:$$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi | :$$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi | ||
)= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi | )= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi | ||
| Line 108: | Line 123: | ||
)\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$ | )\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$ | ||
:$$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$ | ||
| − | + | Considering $g(t = 0) = A \cdot 10 \ \rm kHz$, we get: | |
:$$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$ | :$$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | |
| + | '''(5)''' The second Nyquist criterion states that the Nyquist pulse $g(t)$ has zero crossings at $\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ | ||
| + | *According to the result from '''(4)''' this condition is not fulfilled here. Therefore <u>solution 2</u> is correct. | ||
| Line 118: | Line 135: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.3 Nyquist System Properties^]] |
Latest revision as of 08:16, 20 May 2022
Given by the sketch is the spectrum $G(f)$ of the basic detection pulse, where the parameter $A$ is still to be determined. Among other things it is to be checked whether this basic detection pulse fulfills one of the two Nyquist criteria. These are:
- The first Nyquist criterion is fulfilled if for the spectral function holds:
- $$\sum_{k = -\infty}^{+\infty} G(f - {k}/{T} ) = {\rm const.}$$
- In this case, the pulse $g(t)$ has zero crossings at $t = ν \cdot T$ for all integer values of $ν$ except $ν = 0$. For the entire exercise, $T = 0.1 \, \rm ms$ is assumed.
- If the second Nyquist criterion is satisfied, $g(t)$ has zero crossings at $\pm 1.5 T$, $\pm 2.5 T$, etc.
Notes:
- The exercise belongs to the chapter "Properties of Nyquist Systems".
- The two equations are assumed to be known:
- $$X(f) = \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\hspace{0.15cm}|f| < f_0 \hspace{0.05cm}, \\ {\rm{for}}\hspace{0.15cm}|f| > f_0 \hspace{0.08cm} \\ \end{array} \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} x(t) =2 \cdot A \cdot f_0 \cdot {\rm si}(2 \pi f_0 T) \hspace{0.05cm},\hspace{0.4cm} {\rm si} (x) = \sin(x)/x\hspace{0.05cm},$$
- $$\sin(\alpha) \cdot \cos (\beta) = \frac{1}{2} \cdot \big[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\big] \hspace{0.05cm}.$$
Questions
Solution
- $$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} G(f - \frac{k}{T} ) \hspace{0.05cm}.$$
- The indexing variable $k = 0$ indicates the original spectral function $G(f)$. This is filled in gray.
- The spectrum shifted to the right by the value $1/T = 10\, \rm kHz$ belongs to $k = 1$ and is marked in green, while $k = -1$ leads to the function highlighted in yellow.
- The red and blue areas mark the contributions of the indexing variables $k = 2$ and $k = - 2$.
It can be seen that $G_{\rm Per}(f)$ is constant. From this it follows that the first Nyquist criterion is fulfilled ⇒ solution 1 is correct.
(2) Due to the Fourier integrals the following relation holds:
- $$g(t=0) = \int_{-\infty}^{\infty}G(f) \,{\rm d} f = A \cdot ( 2\,{\rm kHz}+6\,{\rm kHz}+2\,{\rm kHz})= A \cdot 10\,{\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm}A = \frac{g(t=0)}{10\,{\rm kHz}} = \frac{2\,{\rm V}}{10\,{\rm kHz}} \hspace{0.1cm}\underline {= 0.2 \, {\rm mV/Hz}} \hspace{0.05cm}.$$
(3) Let $g(t) = g_{1}(t) +g_{2}(t)$, where
- $g_{1}(t)$ contains the spectral components in the interval $\pm 3 \, \rm kHz$ and
- $g_{2}(t)$ those between $13 \, \rm kHz$ and $15 \, \rm kHz$ (and between $-13 \, \rm kHz$ and $-15 \, \rm kHz$).
With the Fourier correspondence given, the two components are:
- $$g_1(t) \ = \ A \cdot 6\,{\rm kHz} \cdot {\rm si}(\pi \cdot 6\,{\rm kHz} \cdot t) \hspace{0.05cm},$$
- $$g_2(t) \ = \ A \cdot 2\,{\rm kHz} \cdot{\rm si}(\pi \cdot 2\,{\rm kHz} \cdot t) \cdot 2 \cdot {\rm cos}(2 \pi \cdot 14\,{\rm kHz} \cdot t) \hspace{0.05cm}.$$
The second equation follows from the relation:
- $$G_2(f) = \left[ \delta(f + 14\,{\rm kHz}) + \delta(f - 14\,{\rm kHz})\right] \star \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\hspace{0.15cm}|f| < 1\,{\rm kHz} \hspace{0.05cm}, \\ {\rm{for}}\hspace{0.15cm}|f| > 1\,{\rm kHz} \hspace{0.05cm}. \\ \end{array}$$
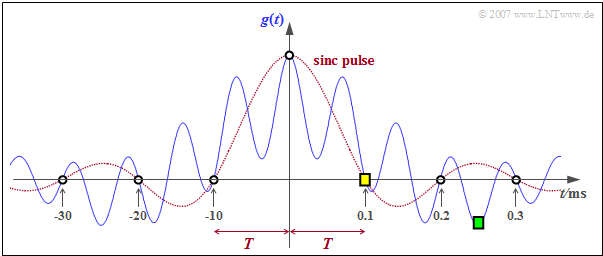
The bottom diagram shows the numerically determined time history $g(t)$. For the time $t = T = 0.1\, \rm ms$ (yellow square) we get:
- $$g_2(t = T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.2 \cdot \pi)\cdot \cos (2.8 \cdot \pi) = \frac{ A \cdot 4\,{\rm kHz}}{0.2 \cdot \pi}\cdot {\rm sin}(0.2 \cdot \pi )\cdot\cos (0.8 \cdot \pi) = \frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot [{\rm sin}(-0.6 \cdot \pi)+ {\rm sin}(\pi)] $$
- $$\Rightarrow \hspace{0.3cm} g_2(t = T ) = -\frac{ A \cdot 10\,{\rm kHz}}{ \pi}\cdot {\rm sin}(0.6 \cdot \pi).$$
For the first component $g_1(t)$, at time $t = T$:
- $$g_1(t = T ) = A \cdot 6\,{\rm kHz} \cdot {\rm sinc}(0.6 )$$
- $$\Rightarrow \hspace{0.3cm}g_1(t = T ) = \frac{ A \cdot 6\,{\rm kHz}}{0.6 \cdot \pi}\cdot {\rm sin}(0.6 \cdot \pi )$$
- $$\Rightarrow \hspace{0.3cm}g_1(t = T ) = - g_2(t = T )$$
- $$\Rightarrow \hspace{0.3cm} g(t = T ) = g_1(t = T ) + g_2(t = T )\hspace{0.1cm}\underline {= 0 } \hspace{0.05cm}.$$
This result is not surprising because of the Nyquist property.
(4) For $t = 2.5 T$ (green square), the following partial results are obtained:
- $$g_1(t = 2.5 T ) = A \cdot 6\,{\rm kHz} \cdot {\rm si}(1.5 \cdot \pi )= \frac{ A \cdot 6\,{\rm kHz}}{1.5 \cdot \pi}\cdot {\rm sin}(1.5 \cdot \pi )= - \frac{ A \cdot 4\,{\rm kHz}}{ \pi}\hspace{0.05cm},$$
- $$g_2(t = 2.5 T ) = 2A \cdot 2\,{\rm kHz} \cdot {\rm si}(0.5 \cdot \pi )\cdot \cos (7 \cdot \pi)=- \frac{ A \cdot 8\,{\rm kHz}}{ \pi} $$
- $$\Rightarrow \hspace{0.3cm} g(t = 2.5 T ) = g_1(t = 2.5 T ) +g_2(t = 2.5 T ) = - \frac{ A \cdot 12\,{\rm kHz}}{ \pi} \hspace{0.05cm}.$$
Considering $g(t = 0) = A \cdot 10 \ \rm kHz$, we get:
- $$\frac{g(t = 2.5 T )}{g(t = 0)} = -\frac{ 1.2}{ \pi} \hspace{0.1cm}\underline {= -0.382 } \hspace{0.05cm}.$$
(5) The second Nyquist criterion states that the Nyquist pulse $g(t)$ has zero crossings at $\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$
- According to the result from (4) this condition is not fulfilled here. Therefore solution 2 is correct.