Difference between revisions of "Aufgaben:Exercise 4.08: Decision Regions at Three Symbols"
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Approximation_of_the_Error_Probability}} |
| − | [[File:P_ID2018__Dig_A_4_8.png|right|frame| | + | [[File:P_ID2018__Dig_A_4_8.png|right|frame|Signal space constellations with $M = 3$ symbols]] |
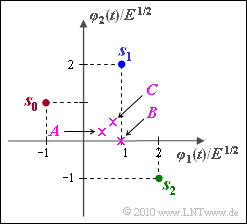
| − | + | We consider a signal space constellation in the two-dimensional space $(N = 2)$ with the signal set: | |
:$$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} | :$$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} | \boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$ | \boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$ | ||
| − | + | in each case referred to the normalization value $\sqrt {E}$. | |
| − | + | The decision regions $I_0$, $I_1$ and $I_2$ are sought, with the following considerations: | |
| − | + | # The region $I_i$ should contain the signal space point $\boldsymbol{s}_i$ ($i = 0,\ 1,\ 2$). | |
| − | + | # The signals $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ are equally probable. | |
| − | + | # The regions are to be determined in such a way that the smallest error probability results for the AWGN channel. | |
| − | + | With these preconditions, the decision boundaries $G_{\it ik}$ between regions $I_i$ and $I_k$ are respectively straight lines exactly midway between $\boldsymbol{s}_i$ and $\boldsymbol{s}_k$ $(i = 0,\ 1,\ 2; \ \ k = 0,\ 1,\ 2; \ \ i ≠ k)$. | |
| − | + | With crosses in the above graph are three received values | |
:$$\boldsymbol{ A } = (0.50, \hspace{0.1cm}0.25)\hspace{0.05cm}, \hspace{0.2cm} | :$$\boldsymbol{ A } = (0.50, \hspace{0.1cm}0.25)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ B } = (1, \hspace{0.1cm}0)\hspace{0.05cm}, \hspace{0.2cm} | \boldsymbol{ B } = (1, \hspace{0.1cm}0)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$ | \boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$ | ||
| − | + | are drawn,nbsp; each of which is to be assigned to a region $I_i$ in subtask '''(5)'''. | |
| − | + | ||
| − | * | + | |
| − | * | + | Notes: |
| + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability|"Approximation of the Error Probability"]]. | ||
| + | |||
| + | * To simplify the notation, the following is used: | ||
:$$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} | :$$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} | ||
y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$ | y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$ | ||
| Line 33: | Line 36: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the equation of the decision boundary $G_{\rm 01}$? |
| − | |type=" | + | |type="()"} |
| − | + $y = 3/2 \, | + | + $y = 3/2 \, -2 \cdot x$, |
- $y = x/3$, | - $y = x/3$, | ||
| − | - $y = \, | + | - $y = \, -3/4 + 3/2 \cdot x$. |
| − | { | + | {What is the equation of the decision boundary $G_{\rm 02}$? |
| − | |type=" | + | |type="()"} |
| − | - $y = 3/2 \, | + | - $y = 3/2 \, -2 \cdot x$, |
- $y = x/3$, | - $y = x/3$, | ||
| − | + $y = \, | + | + $y = \, -3/4 + 3/2 \cdot x$. |
| − | { | + | {What is the equation of the decision boundary $G_{\rm 12}$? |
| − | |type=" | + | |type="()"} |
| − | - $y = 3/2 \, | + | - $y = 3/2 \, -2 \cdot x$, |
+ $y = x/3$, | + $y = x/3$, | ||
| − | - $y = \, | + | - $y = \, -3/4 + 3/2 \cdot x$. |
| − | { | + | {Sketch the three decision regions $I_0$, $I_1$ and $I_2$. Do the decision boundaries $G_{\rm 01}$, $G_{\rm 02}$ and $G_{\rm 12}$ intersect at a point? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {Which of the following decisions are correct? |
|type="[]"} | |type="[]"} | ||
| − | + $\boldsymbol{A} = (0.5, 0.25)$ | + | + $\boldsymbol{A} = (0.5,\ 0.25)$ belongs to region $I_0$. |
| − | + $\boldsymbol{B} = (1, 0)$ | + | + $\boldsymbol{B} = (1,\ 0)$ belongs to region $I_2$. |
| − | + $\boldsymbol{C} = (0.75, 0.5)$ | + | + $\boldsymbol{C} = (0.75,\ 0.5)$ belongs to region $I_1$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
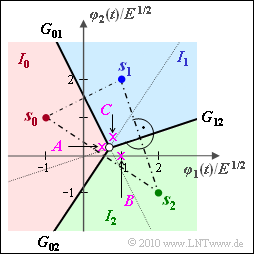
| − | '''(1)''' | + | [[File:P_ID2038__Dig_A_4_8d.png|right|frame|Decision regions]] |
| − | '''(2)''' | + | '''(1)''' <u>Solution 1</u> is correct: |
| − | '''(3)''' | + | *The connecting line between the signal points $\boldsymbol{s}_0 = (–1,\ 1)$ and $\boldsymbol{s}_1 = (1,\ 2)$ has the gradient $1/2$ (see diagram). |
| − | '''(4)''' | + | *The decision boundary intersects the connecting line at $(\boldsymbol{s}_0 + \boldsymbol{s}_1)/2 = (0,\ 1.5)$ and has the gradient $2$ $($rotation of the connecting line by $90^\circ)$. |
| − | '''(5)''' | + | *From this follows: $y = 1.5 - 2 x \hspace{0.05cm}.$ |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Solution 3</u> is correct: | ||
| + | *The connecting line between $\boldsymbol{s}_0 = (–1,\ 1)$ and $\boldsymbol{s}_2 = (2,\ 1)$ has the gradient $–2/3$ and intersects the decision boundary $G_{\rm 02}$ $($with gradient $3/2)$ at $(0.5,\ 0)$. | ||
| + | *From this follows: $y = {3}/{2} \left ( x - {1}/{2} \right ) | ||
| + | = -{3}/{4} + {3}/{2} \cdot x\hspace{0.05cm}.$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Here <u>solution 2</u> is applicable: | ||
| + | *The line connecting $\boldsymbol{s}_1 = (1,\ 2)$ and $\boldsymbol{s}_2 = (2, \, –1)$ intersects the decision boundary $G_{\rm 12}$ at $(1.5,\ 0.5)$ and has gradient $–3$. | ||
| + | *Consequently, the gradient of $G_{\rm 12} = 1/3$ and the equation of the decision boundary $G_{\rm 12}$ is: | ||
| + | :$$y - {1}/{2} = {1}/{3} \cdot \left ( x - {3}/{2} \right ) | ||
| + | = {x}/{3} - {1}/{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y = {x}/{3} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The graph already shows the correct answer ⇒ <u>YES</u>. | ||
| + | *The intersection of $G_{\rm 01}$ and $G_{\rm 12}$ (white circle) is at $(9/14,\ 3/14)$, because of | ||
| + | :$${3}/{2} - 2 x = {x}/{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | {3}/{2} = {7}/{3} \cdot x \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} y = {3}/{14} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The straight line $G_{\rm 02}$ also passes through this point: | ||
| + | :$$y(x = {9}/{14}) =-{3}/{4} + {3}/{2} \cdot x = -{3}/{4} + {3}/{2} \cdot {9}/{14} =\frac{-21+27}{28}= {3}/{14} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' According to the graph: <u>all statements mentioned are correct</u>. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.3 BER Approximation^]] |
Latest revision as of 12:56, 3 September 2022
We consider a signal space constellation in the two-dimensional space $(N = 2)$ with the signal set:
- $$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$
in each case referred to the normalization value $\sqrt {E}$.
The decision regions $I_0$, $I_1$ and $I_2$ are sought, with the following considerations:
- The region $I_i$ should contain the signal space point $\boldsymbol{s}_i$ ($i = 0,\ 1,\ 2$).
- The signals $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ are equally probable.
- The regions are to be determined in such a way that the smallest error probability results for the AWGN channel.
With these preconditions, the decision boundaries $G_{\it ik}$ between regions $I_i$ and $I_k$ are respectively straight lines exactly midway between $\boldsymbol{s}_i$ and $\boldsymbol{s}_k$ $(i = 0,\ 1,\ 2; \ \ k = 0,\ 1,\ 2; \ \ i ≠ k)$.
With crosses in the above graph are three received values
- $$\boldsymbol{ A } = (0.50, \hspace{0.1cm}0.25)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B } = (1, \hspace{0.1cm}0)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$
are drawn,nbsp; each of which is to be assigned to a region $I_i$ in subtask (5).
Notes:
- The exercise belongs to the chapter "Approximation of the Error Probability".
- To simplify the notation, the following is used:
- $$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$
Questions
Solution
(1) Solution 1 is correct:
- The connecting line between the signal points $\boldsymbol{s}_0 = (–1,\ 1)$ and $\boldsymbol{s}_1 = (1,\ 2)$ has the gradient $1/2$ (see diagram).
- The decision boundary intersects the connecting line at $(\boldsymbol{s}_0 + \boldsymbol{s}_1)/2 = (0,\ 1.5)$ and has the gradient $2$ $($rotation of the connecting line by $90^\circ)$.
- From this follows: $y = 1.5 - 2 x \hspace{0.05cm}.$
(2) Solution 3 is correct:
- The connecting line between $\boldsymbol{s}_0 = (–1,\ 1)$ and $\boldsymbol{s}_2 = (2,\ 1)$ has the gradient $–2/3$ and intersects the decision boundary $G_{\rm 02}$ $($with gradient $3/2)$ at $(0.5,\ 0)$.
- From this follows: $y = {3}/{2} \left ( x - {1}/{2} \right ) = -{3}/{4} + {3}/{2} \cdot x\hspace{0.05cm}.$
(3) Here solution 2 is applicable:
- The line connecting $\boldsymbol{s}_1 = (1,\ 2)$ and $\boldsymbol{s}_2 = (2, \, –1)$ intersects the decision boundary $G_{\rm 12}$ at $(1.5,\ 0.5)$ and has gradient $–3$.
- Consequently, the gradient of $G_{\rm 12} = 1/3$ and the equation of the decision boundary $G_{\rm 12}$ is:
- $$y - {1}/{2} = {1}/{3} \cdot \left ( x - {3}/{2} \right ) = {x}/{3} - {1}/{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y = {x}/{3} \hspace{0.05cm}.$$
(4) The graph already shows the correct answer ⇒ YES.
- The intersection of $G_{\rm 01}$ and $G_{\rm 12}$ (white circle) is at $(9/14,\ 3/14)$, because of
- $${3}/{2} - 2 x = {x}/{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {3}/{2} = {7}/{3} \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y = {3}/{14} \hspace{0.05cm}.$$
- The straight line $G_{\rm 02}$ also passes through this point:
- $$y(x = {9}/{14}) =-{3}/{4} + {3}/{2} \cdot x = -{3}/{4} + {3}/{2} \cdot {9}/{14} =\frac{-21+27}{28}= {3}/{14} \hspace{0.05cm}.$$
(5) According to the graph: all statements mentioned are correct.