Difference between revisions of "Aufgaben:Exercise 2.1Z: About the Equivalent Bitrate"
From LNTwww
| (18 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Basics_of_Coded_Transmission |
}} | }} | ||
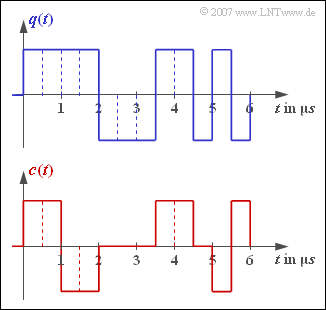
| − | [[File:P_ID1309__Dig_Z_2_1.png|right|frame| | + | [[File:P_ID1309__Dig_Z_2_1.png|right|frame|Source signal (top) and encoder signal (bottom)]] |
| − | + | The upper diagram shows the source signal $q(t)$ of a redundancy-free binary source with bit duration $T_{q}$ and bit rate $R_{q}$. The two signal parameters $T_{q}$ and $R_{q}$ can be taken from the sketch. | |
| − | + | *This binary signal is coded symbol-by-symbol and results in the encoder signal $c(t)$ drawn below. | |
| − | + | *All possible encoder symbols occur in the signal section of duration $6 \ \rm µ s$ shown. | |
| + | *The level number $M_{c}$ and the symbol duration $T_{c}$ can be used to specify the equivalent bit rate of the encoder signal: | ||
:$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$ | :$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$ | ||
| − | + | From this, one obtains the relative redundancy of the code if one assumes, as here, that the source itself is redundancy-free: | |
:$$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$ | :$$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$ | ||
| − | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Basics_of_Coded_Transmission|"Basics of Coded Transmission"]]. | ||
| + | |||
| + | *The transmission code considered here is the second order bipolar code, but this is not important for the solution of this exercise. | ||
| − | |||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Specify bit duration $(T_{q})$ and bit rate $(R_{q})$ of the source. | ||
| + | |type="{}"} | ||
| + | $T_{q} \ = \ $ { 0.5 3% } $\ \rm µ s $ | ||
| + | $R_{q} \ = \ $ { 2 3% } $\ \rm Mbit/s $ | ||
| + | |||
| + | {What are the symbol duration $(T_{c})$ and level number $(M_{c})$ of the encoder signal? | ||
| + | |type="{}"} | ||
| + | $T_{c} \ = \ $ { 0.5 3% } $\ \rm µ s $ | ||
| + | $M_{c} \ = \ $ { 3 3% } | ||
| − | { | + | {What is the equivalent bit rate $R_{c}$ of the encoder signal? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $R_{c} \ = \ $ { 3.17 3% } $\ \rm Mbit/s $ |
| + | {Specify the relative redundancy of the code. | ||
| + | |type="{}"} | ||
| + | $r_{c} \ = \ $ { 36.9 3% } $\ \% $ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The bit duration $T_{q} = \underline{0.5\ \rm µ s}$ can be taken from the graphic. |
| − | '''(2)''' | + | *Since the source is binary and redundancy-free, the following applies to the bit rate of the source: |
| − | '''(3)''' | + | :$$R_{q}= 1/T_{q}\ \underline{= 2\ \rm Mbit/s}.$$ |
| − | '''(4)''' | + | |
| − | + | ||
| − | + | '''(2)''' For symbol-wise coding, $T_{c} = T_{q}$ always applies. | |
| + | *Thus, in the present example, $T_{c}\ \underline{ = 0.5\ \rm µ s}$ is valid. | ||
| + | *The level number $M_{c}\ \underline{ = 3}$ can be read from the sketch below. | ||
| + | |||
| + | |||
| + | '''(3)''' The symbol rate of the encoder signal is $2 \cdot 10^{6}$ ternary symbols per second. | ||
| + | *For the equivalent bit rate, the following applies: | ||
| + | :$$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' For relative code redundancy, when the source is redundancy-free, the general rule is: | ||
| + | :$$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$ | ||
| + | *In the case of the second order biploar code considered here, with parameters $T_{c} = T_{q}$ and $M_{c} = 3$, the following holds: | ||
| + | :$$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 50: | Line 76: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.1 Basics of Coded Transmission^]] |
Latest revision as of 15:54, 3 June 2022
The upper diagram shows the source signal $q(t)$ of a redundancy-free binary source with bit duration $T_{q}$ and bit rate $R_{q}$. The two signal parameters $T_{q}$ and $R_{q}$ can be taken from the sketch.
- This binary signal is coded symbol-by-symbol and results in the encoder signal $c(t)$ drawn below.
- All possible encoder symbols occur in the signal section of duration $6 \ \rm µ s$ shown.
- The level number $M_{c}$ and the symbol duration $T_{c}$ can be used to specify the equivalent bit rate of the encoder signal:
- $$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$
From this, one obtains the relative redundancy of the code if one assumes, as here, that the source itself is redundancy-free:
- $$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Basics of Coded Transmission".
- The transmission code considered here is the second order bipolar code, but this is not important for the solution of this exercise.
Questions
Solution
(1) The bit duration $T_{q} = \underline{0.5\ \rm µ s}$ can be taken from the graphic.
- Since the source is binary and redundancy-free, the following applies to the bit rate of the source:
- $$R_{q}= 1/T_{q}\ \underline{= 2\ \rm Mbit/s}.$$
(2) For symbol-wise coding, $T_{c} = T_{q}$ always applies.
- Thus, in the present example, $T_{c}\ \underline{ = 0.5\ \rm µ s}$ is valid.
- The level number $M_{c}\ \underline{ = 3}$ can be read from the sketch below.
(3) The symbol rate of the encoder signal is $2 \cdot 10^{6}$ ternary symbols per second.
- For the equivalent bit rate, the following applies:
- $$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$
(4) For relative code redundancy, when the source is redundancy-free, the general rule is:
- $$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$
- In the case of the second order biploar code considered here, with parameters $T_{c} = T_{q}$ and $M_{c} = 3$, the following holds:
- $$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$