Difference between revisions of "Aufgaben:Exercise 2.4: Dual Code and Gray Code"
| (14 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Redundancy-Free_Coding |
}} | }} | ||
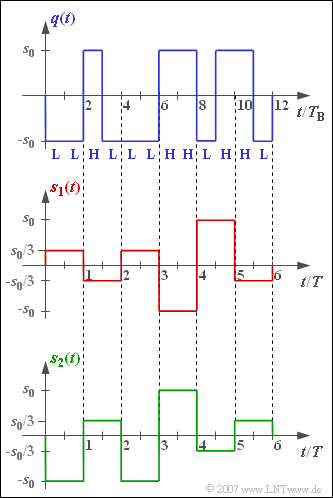
| − | [[File:P_ID1325__Dig_A_2_4.png|right|frame| | + | [[File:P_ID1325__Dig_A_2_4.png|right|frame|Quaternary signals with dual and Gray coding]] |
| − | + | The two shown signals $s_{1}(t)$ and $s_{2}(t)$ are two different realizations of a redundancy-free quaternary transmitted signal, both derived from the blue drawn binary source signal $q(t)$. | |
| + | |||
| + | For one of the transmitted signals, the so-called '''dual code''' with mapping | ||
:$$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} | :$$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} | ||
\mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$ | \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$ | ||
| − | + | was used, for the other one a certain form of a '''Gray code'''. This is characterized by the fact that the binary representation of adjacent amplitude values always differ only in a single bit. | |
| + | |||
| + | The solution of the exercise should be based on the following assumptions: | ||
| + | *The amplitude levels are $±3\, \rm V$ and $±1 \, \rm V$. | ||
| + | |||
| + | *The decision thresholds lie in the middle between two adjacent amplitude values, i.e. at $–2\, \rm V$, $0\, \rm V$ and $+2\, \rm V$. | ||
| + | |||
| + | *The noise rms value $\sigma_{d}$ is to be chosen so that the falsification probability from the outer symbol $(+s_0)$ to the nearest symbol $(+s_{0}/3)$ is exactly $p = 1\%$. | ||
| − | + | *Falsification to non-adjacent symbols can be excluded; in the case of Gaussian perturbations, this simplification is always allowed in practice. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | One distinguishes in principle between | ||
| + | *the "symbol error probability" $p_{\rm S}$ (related to the quaternary signal) and | ||
| + | *the "bit error probability" $p_{B}$ (related to the binary source signal). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | Notes: | ||
| + | *The exercise is part of the chapter [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung|"Basics of Coded Transmission"]]. | ||
| + | |||
| + | *Reference is also made to the chapter [[Digital_Signal_Transmission/Redundanzfreie_Codierung|"Redundancy-Free Coding"]]. | ||
| + | |||
| + | *For numerical evaluation of the Q–function you can use the HTML5/JavaScript applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]]. | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the signals $s_{1}(t)$ or $s_{2}(t)$ uses '''Gray coding'''? |
|type="[]"} | |type="[]"} | ||
| − | +$s_{1}(t)$ | + | +$s_{1}(t)$ uses Gray coding. |
| − | -$s_{2}(t)$ | + | -$s_{2}(t)$ uses Gray coding. |
| − | { | + | {Determine the noise rms value from the given condition. |
|type="{}"} | |type="{}"} | ||
$\sigma_{d} \ = \ $ { 0.43 3% } $\ \rm V$ | $\sigma_{d} \ = \ $ { 0.43 3% } $\ \rm V$ | ||
| − | { | + | {What is the symbol error probability using the '''Gray code'''? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 1.5 3% } $\ \%$ | $p_{\rm S} \ = \ $ { 1.5 3% } $\ \%$ | ||
| − | { | + | {What is the bit error probability with the Gray code? |
|type="{}"} | |type="{}"} | ||
$p_{\rm B} \ = \ $ { 0.75 3% } $\ \%$ | $p_{\rm B} \ = \ $ { 0.75 3% } $\ \%$ | ||
| − | { | + | {What is the symbol error probability with the '''dual code'''? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 1.5 3% } $\ \%$ | $p_{\rm S} \ = \ $ { 1.5 3% } $\ \%$ | ||
| − | { | + | {What is the bit error probability with the dual code? |
|type="{}"} | |type="{}"} | ||
$p_{\rm B} \ = \ $ { 1 3% } $\ \%$ | $p_{\rm B} \ = \ $ { 1 3% } $\ \%$ | ||
| Line 59: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' In the signal $s_{2}(t)$ one recognizes the realization of the dual code indicated at the beginning. On the other hand, in the signal $s_{2}(t)$ a Gray code $\Rightarrow$ <u>solution 1</u> with the following mapping was used: |
| − | :$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0. | + | :$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$ |
| − | '''(2)''' | + | |
| + | '''(2)''' Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that: | ||
:$$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$ | :$$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| + | '''(3)''' The two outer symbols are each falsified with probability $p$, the two inner symbols with double probability $(2p)$. By averaging considering equal symbol occurrence probabilities, we obtain | ||
:$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| + | '''(4)''' Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained: | ||
:$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$ | ||
| − | |||
| − | '''(6)''' | + | '''(5)''' When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask '''(3)''', we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$. |
| + | |||
| + | |||
| + | '''(6)''' The two outer symbols are falsified with $p$ and lead to only one bit error each even with dual code. | ||
| + | * The inner symbols are falsified with $2p$ and now lead to $1.5$ bit errors on average. | ||
| + | *Taking into account the factor $2$ in the denominator – see subtask '''(2)''' – we thus obtain for the bit error probability of the dual code: | ||
:$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$ | ||
| Line 82: | Line 99: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.2 Redundancy-Free Coding^]] |
Latest revision as of 16:46, 16 May 2022
The two shown signals $s_{1}(t)$ and $s_{2}(t)$ are two different realizations of a redundancy-free quaternary transmitted signal, both derived from the blue drawn binary source signal $q(t)$.
For one of the transmitted signals, the so-called dual code with mapping
- $$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$
was used, for the other one a certain form of a Gray code. This is characterized by the fact that the binary representation of adjacent amplitude values always differ only in a single bit.
The solution of the exercise should be based on the following assumptions:
- The amplitude levels are $±3\, \rm V$ and $±1 \, \rm V$.
- The decision thresholds lie in the middle between two adjacent amplitude values, i.e. at $–2\, \rm V$, $0\, \rm V$ and $+2\, \rm V$.
- The noise rms value $\sigma_{d}$ is to be chosen so that the falsification probability from the outer symbol $(+s_0)$ to the nearest symbol $(+s_{0}/3)$ is exactly $p = 1\%$.
- Falsification to non-adjacent symbols can be excluded; in the case of Gaussian perturbations, this simplification is always allowed in practice.
One distinguishes in principle between
- the "symbol error probability" $p_{\rm S}$ (related to the quaternary signal) and
- the "bit error probability" $p_{B}$ (related to the binary source signal).
Notes:
- The exercise is part of the chapter "Basics of Coded Transmission".
- Reference is also made to the chapter "Redundancy-Free Coding".
- For numerical evaluation of the Q–function you can use the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
Questions
Solution
- $$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$
(2) Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that:
- $$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$
(3) The two outer symbols are each falsified with probability $p$, the two inner symbols with double probability $(2p)$. By averaging considering equal symbol occurrence probabilities, we obtain
- $$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$
(4) Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained:
- $$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$
(5) When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask (3), we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$.
(6) The two outer symbols are falsified with $p$ and lead to only one bit error each even with dual code.
- The inner symbols are falsified with $2p$ and now lead to $1.5$ bit errors on average.
- Taking into account the factor $2$ in the denominator – see subtask (2) – we thus obtain for the bit error probability of the dual code:
- $$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$