Difference between revisions of "Aufgaben:Exercise 2.5: Ternary Signal Transmission"
From LNTwww
| (25 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Redundancy-Free_Coding |
}} | }} | ||
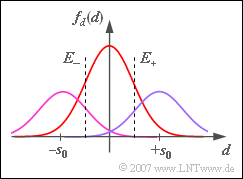
| − | [[File:P_ID1327__Dig_A_2_5.png|right|frame| | + | [[File:P_ID1327__Dig_A_2_5.png|right|frame|Probability density function $\rm (PDF)$ of a noisy ternary signal]] |
| − | + | A ternary transmission system $(M = 3)$ with the possible amplitude values $-s_0$, $0$ and $+s_0$ is considered. | |
| + | *During transmission, additive Gaussian noise with rms value $\sigma_d$ is added to the signal. | ||
| − | + | *The recovery of the three-level digital signal at the receiver is done with the help of two decision thresholds at $E_{–}$ and $E_{+}$. | |
| + | |||
| + | *First, the occurrence probabilities of the three input symbols are assumed to be equally probable: | ||
:$$p_{\rm -} = {\rm Pr}(-s_0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm 0} = {\rm Pr}(0) = {1}/{ 3}, | :$$p_{\rm -} = {\rm Pr}(-s_0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm 0} = {\rm Pr}(0) = {1}/{ 3}, | ||
\hspace{0.15cm} p_{\rm +} = {\rm Pr}(+s_0) ={1}/{ 3}\hspace{0.05cm}.$$ | \hspace{0.15cm} p_{\rm +} = {\rm Pr}(+s_0) ={1}/{ 3}\hspace{0.05cm}.$$ | ||
| − | + | *For the time being, the decision thresholds are centered at $E_{–} = \, –s_0/2$ and $E_{+} = +s_0/2$. | |
| + | |||
| + | *From subtask '''(3)''' on, the symbol probabilities are $p_{–} = p_+ = 1/4$ and $p_0 = 1/2$, as shown in the diagram. | ||
| + | |||
| + | *For this constellation, the symbol error probability $p_{\rm S}$ is to be minimized by varying the decision thresholds $E_{–}$ and $E_+$. | ||
| + | |||
| − | |||
| − | + | ||
| − | * | + | Notes: |
| − | * | + | * The exercise refers to the chapter [[Digital_Signal_Transmission/Redundancy-Free_Coding|"Redundancy-Free Coding"]]. |
| + | |||
| + | * For the symbol error probability $p_{\rm S}$ of a $M$–level transmission system | ||
| + | :*with equally probable input symbols | ||
| + | :*and threshold values exactly in the middle between two adjacent amplitude levels holds: | ||
:$$p_{\rm S} = | :$$p_{\rm S} = | ||
\frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right) | \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * You can numerically determine the error probability values according to our applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]]. |
| − | * | + | |
| − | + | * To check your results, use our (German language) SWF applet [[Applets:Fehlerwahrscheinlichkeit|"Symbol error probability of digital communications systems"]]. | |
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What symbol error probability results with the (normalized) noise rms value $\sigma_d/s_0 = 0.25$ for equally probable symbols? |
| − | |type=" | + | |type="{}"} |
| − | + | + | $p_0 = 1/3, \ \sigma_d = 0.25 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ ${ 3 3% } $\ \%$ |
| − | + | ||
| + | {How does the symbol error probability change with $\sigma_d/s_0 = 0.5$? | ||
| + | |type="{}"} | ||
| + | $p_0 = 1/3, \ \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ ${ 21.2 3% } $\ \%$ | ||
| + | |||
| + | {What value results with $p_{–} = p_+ = 0.25$ and $p_0 = 0.5$? | ||
| + | |type="{}"} | ||
| + | $p_0 = 1/2, \ \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ ${ 23.8 3% } $\ \%$ | ||
| − | { | + | {Determine the optimal thresholds $E_+$ and $E_{–} = \, –E_+$ for $p_0 = 1/2$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_0 = 1/2, \ \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ ${ 0.673 3% } |
| + | |||
| + | {What is the symbol error probability for optimal thresholds? | ||
| + | |type="{}"} | ||
| + | ${\rm optimal \ thresholds} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ ${ 21.7 3% } $\ \%$ | ||
| + | |||
| + | {What are the optimal thresholds for $p_0 = 0.2$ and $ p_{–} = p_+ = 0.4$? | ||
| + | |type="{}"} | ||
| + | $p_0 = 0.2, \ \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ ${ 0.327 3% } | ||
| + | |||
| + | {What is the symbol error probability now? Interpretation. | ||
| + | |type="{}"} | ||
| + | ${\rm optimal \ thresholds} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ ${ 17.4 3% } $\ \%$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the given equation, with $M = 3$ and $\sigma_d/s_0 = 0.25$: |
| − | '''(2)''' | + | :$$p_{\rm S} = |
| − | '''(3)''' | + | \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot |
| − | '''(4)''' | + | \sigma_d}}\right)= {4}/{ 3}\cdot {\rm Q}(2) ={4}/{ 3}\cdot 0.0228\hspace{0.15cm}\underline {\approx 3 \,\%} |
| − | '''(5)''' | + | \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | '''(2)''' When the noise rms value is doubled, the error probability increases significantly: | ||
| + | :$$p_{\rm S} = {4}/{ 3}\cdot {\rm Q}(1)= {4}/{ 3}\cdot 0.1587 \hspace{0.15cm}\underline {\approx 21.2 \,\%} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' The two outer symbols are each falsified with probability $p = {\rm Q}(s_0/(2 \cdot \sigma_d)) = 0.1587$. | ||
| + | *The falsification probability of the symbol $0$ is twice as large (it is limited by two thresholds). | ||
| + | * Considering the individual symbol probabilities, we obtain: | ||
| + | :$$p_{\rm S} = {1}/{ 4}\cdot p + {1}/{ 2}\cdot 2p +{1}/{ 4}\cdot p = 1.5 \cdot p = 1.5 \cdot 0.1587 | ||
| + | \hspace{0.15cm}\underline {\approx | ||
| + | 23.8 \,\%} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
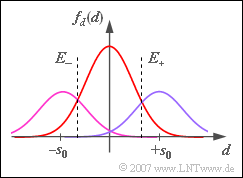
| + | '''(4)''' Since the symbol $0$ occurs more frequently and can also be falsified in both directions, the thresholds should be shifted outward. | ||
| + | *The optimal decision threshold $E_{\rm +, \ opt}$ is obtained from the intersection of the two Gaussian functions shown in the graph. It must hold: | ||
| + | |||
| + | [[File:P_ID1328__Dig_A_2_5e.png|right|frame|Optimal thresholds for subtask '''(4)''']] | ||
| + | |||
| + | :$$\frac{ 1/2}{ \sqrt{2\pi} \cdot \sigma_d} \cdot {\rm exp} \left[ - \frac{ E_{\rm +}^2}{2 \cdot \sigma_d^2}\right] | ||
| + | = \frac{ 1/4}{ \sqrt{2\pi} \cdot \sigma_d} \cdot {\rm exp} \left[ - \frac{ (s_0 -E_{\rm +})^2}{2 \cdot \sigma_d^2}\right]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\rm exp} \left[ \frac{ (s_0 -E_{\rm +})^2 - E_{\rm +}^2}{2 \cdot | ||
| + | \sigma_d^2}\right]= {1}/{ 2} | ||
| + | \Rightarrow \hspace{0.3cm} {\rm exp} \left[ \frac{ 1 -2 \cdot E_{\rm +}/s_0}{2 \cdot | ||
| + | \sigma_d^2/s_0^2}\right]= {1}/{ 2}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}\frac{ E_{\rm +}}{s_0}= \frac{1} | ||
| + | { 2}+ \frac{\sigma_d^2} {s_0^2} \cdot {\rm ln}(2)\hspace{0.15cm}\underline {=0.673}\hspace{0.15cm}\approx | ||
| + | {2}/ {3} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Using the approximate result from subtask '''(4)''', we obtain: | ||
| + | :$$p_{\rm S} \ = \ | ||
| + | { 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{ | ||
| + | \sigma_d}}\right)+ 2 \cdot { 1}/{2} \cdot {\rm Q} \left( {\frac{2s_0/3}{ | ||
| + | \sigma_d}}\right) +{ 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{ | ||
| + | \sigma_d}}\right)$$ | ||
| + | [[File:P_ID1329__Dig_A_2_5g.png|right|frame|Optimal thresholds for subtask '''(6)''']] | ||
| + | |||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm}p_{\rm S} \ = \ = { 1}/{2} \cdot {\rm Q} \left( 2/3 \right)+ {\rm Q} \left( 4/3 | ||
| + | \right)= | ||
| + | { 1}/{2} \cdot 0.251 + 0.092 \hspace{0.15cm}\underline {\approx 21.7 \,\%} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
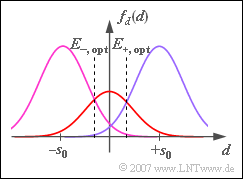
| + | '''(6)''' After a similar calculation as in subtask '''(4)''' we get | ||
| + | *$E_+ = 1 \, –0.0673 \ \underline{= 0.327} \approx 1/3$. | ||
| + | *$E_{–} = \, –E_+$ is still valid. | ||
| + | |||
| + | |||
| + | |||
| + | '''(7)''' Similar to the solution for subtask '''(5)''', we now obtain: | ||
| + | :$$p_{\rm S} \ = \ 0.4 \cdot {\rm Q} \left( 4/3 \right)+ 2 \cdot 0.2 \cdot{\rm Q} \left( 2/3 | ||
| + | \right)+0.4 \cdot {\rm Q} \left( 4/3 \right)$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}p_{\rm S} \ = \ | ||
| + | 0.4 \cdot (0.092 + 0.251 + 0.092) | ||
| + | \hspace{0.15cm}\underline {\approx 17.4 \,\%} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | $\text{Discussion of the result:}$ | ||
| + | *Accordingly, there is a smaller symbol error probability $(17.4 \ \%$ versus $21.2 \ \%)$ than with equal probability amplitude coefficients. | ||
| + | |||
| + | *However, redundancy-free coding is no longer present, even if the amplitude coefficients are statistically independent of each other. | ||
| + | |||
| + | *While for equally probable ternary symbols | ||
| + | :*the entropy is $H = {\rm log}_2(3) = 1.585 \ {\rm bit/ternary \ symbol}$ | ||
| + | :*from which the equivalent bit rate can be calculated according to $R_{\rm B} = H/T$, | ||
| + | :*here applies with probabilities $p_0 = 0.2$ and $p_{–} = p_+ = 0.4$: | ||
| + | ::$$H \ = \ 0.2 \cdot {\rm log_2} (5) + 2 \cdot 0.4 \cdot {\rm log_2} (2.5)= 0.2 \cdot 2.322 + 0.8 \cdot 1.322 \hspace{0.15cm}\underline {\approx 1.522\,\, {\rm | ||
| + | bit/ternary \ symbol}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Thus, the equivalent bit rate here is $\approx 4 \ \%$ smaller than the maximum possible equivalent bit rate for $M = 3$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.2 Redundancy-Free Coding^]] |
Latest revision as of 16:19, 3 June 2022
A ternary transmission system $(M = 3)$ with the possible amplitude values $-s_0$, $0$ and $+s_0$ is considered.
- During transmission, additive Gaussian noise with rms value $\sigma_d$ is added to the signal.
- The recovery of the three-level digital signal at the receiver is done with the help of two decision thresholds at $E_{–}$ and $E_{+}$.
- First, the occurrence probabilities of the three input symbols are assumed to be equally probable:
- $$p_{\rm -} = {\rm Pr}(-s_0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm 0} = {\rm Pr}(0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm +} = {\rm Pr}(+s_0) ={1}/{ 3}\hspace{0.05cm}.$$
- For the time being, the decision thresholds are centered at $E_{–} = \, –s_0/2$ and $E_{+} = +s_0/2$.
- From subtask (3) on, the symbol probabilities are $p_{–} = p_+ = 1/4$ and $p_0 = 1/2$, as shown in the diagram.
- For this constellation, the symbol error probability $p_{\rm S}$ is to be minimized by varying the decision thresholds $E_{–}$ and $E_+$.
Notes:
- The exercise refers to the chapter "Redundancy-Free Coding".
- For the symbol error probability $p_{\rm S}$ of a $M$–level transmission system
- with equally probable input symbols
- and threshold values exactly in the middle between two adjacent amplitude levels holds:
- $$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right) \hspace{0.05cm}.$$
- You can numerically determine the error probability values according to our applet "Complementary Gaussian Error Functions".
- To check your results, use our (German language) SWF applet "Symbol error probability of digital communications systems".
Questions
Solution
(1) According to the given equation, with $M = 3$ and $\sigma_d/s_0 = 0.25$:
- $$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right)= {4}/{ 3}\cdot {\rm Q}(2) ={4}/{ 3}\cdot 0.0228\hspace{0.15cm}\underline {\approx 3 \,\%} \hspace{0.05cm}.$$
(2) When the noise rms value is doubled, the error probability increases significantly:
- $$p_{\rm S} = {4}/{ 3}\cdot {\rm Q}(1)= {4}/{ 3}\cdot 0.1587 \hspace{0.15cm}\underline {\approx 21.2 \,\%} \hspace{0.05cm}.$$
(3) The two outer symbols are each falsified with probability $p = {\rm Q}(s_0/(2 \cdot \sigma_d)) = 0.1587$.
- The falsification probability of the symbol $0$ is twice as large (it is limited by two thresholds).
- Considering the individual symbol probabilities, we obtain:
- $$p_{\rm S} = {1}/{ 4}\cdot p + {1}/{ 2}\cdot 2p +{1}/{ 4}\cdot p = 1.5 \cdot p = 1.5 \cdot 0.1587 \hspace{0.15cm}\underline {\approx 23.8 \,\%} \hspace{0.05cm}.$$
(4) Since the symbol $0$ occurs more frequently and can also be falsified in both directions, the thresholds should be shifted outward.
- The optimal decision threshold $E_{\rm +, \ opt}$ is obtained from the intersection of the two Gaussian functions shown in the graph. It must hold:
- $$\frac{ 1/2}{ \sqrt{2\pi} \cdot \sigma_d} \cdot {\rm exp} \left[ - \frac{ E_{\rm +}^2}{2 \cdot \sigma_d^2}\right] = \frac{ 1/4}{ \sqrt{2\pi} \cdot \sigma_d} \cdot {\rm exp} \left[ - \frac{ (s_0 -E_{\rm +})^2}{2 \cdot \sigma_d^2}\right]$$
- $$\Rightarrow \hspace{0.3cm} {\rm exp} \left[ \frac{ (s_0 -E_{\rm +})^2 - E_{\rm +}^2}{2 \cdot \sigma_d^2}\right]= {1}/{ 2} \Rightarrow \hspace{0.3cm} {\rm exp} \left[ \frac{ 1 -2 \cdot E_{\rm +}/s_0}{2 \cdot \sigma_d^2/s_0^2}\right]= {1}/{ 2}$$
- $$\Rightarrow \hspace{0.3cm}\frac{ E_{\rm +}}{s_0}= \frac{1} { 2}+ \frac{\sigma_d^2} {s_0^2} \cdot {\rm ln}(2)\hspace{0.15cm}\underline {=0.673}\hspace{0.15cm}\approx {2}/ {3} \hspace{0.05cm}.$$
(5) Using the approximate result from subtask (4), we obtain:
- $$p_{\rm S} \ = \ { 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{ \sigma_d}}\right)+ 2 \cdot { 1}/{2} \cdot {\rm Q} \left( {\frac{2s_0/3}{ \sigma_d}}\right) +{ 1}/{4} \cdot {\rm Q} \left( {\frac{s_0/3}{ \sigma_d}}\right)$$
- $$\Rightarrow \hspace{0.3cm}p_{\rm S} \ = \ = { 1}/{2} \cdot {\rm Q} \left( 2/3 \right)+ {\rm Q} \left( 4/3 \right)= { 1}/{2} \cdot 0.251 + 0.092 \hspace{0.15cm}\underline {\approx 21.7 \,\%} \hspace{0.05cm}.$$
(6) After a similar calculation as in subtask (4) we get
- $E_+ = 1 \, –0.0673 \ \underline{= 0.327} \approx 1/3$.
- $E_{–} = \, –E_+$ is still valid.
(7) Similar to the solution for subtask (5), we now obtain:
- $$p_{\rm S} \ = \ 0.4 \cdot {\rm Q} \left( 4/3 \right)+ 2 \cdot 0.2 \cdot{\rm Q} \left( 2/3 \right)+0.4 \cdot {\rm Q} \left( 4/3 \right)$$
- $$\Rightarrow \hspace{0.3cm}p_{\rm S} \ = \ 0.4 \cdot (0.092 + 0.251 + 0.092) \hspace{0.15cm}\underline {\approx 17.4 \,\%} \hspace{0.05cm}.$$
$\text{Discussion of the result:}$
- Accordingly, there is a smaller symbol error probability $(17.4 \ \%$ versus $21.2 \ \%)$ than with equal probability amplitude coefficients.
- However, redundancy-free coding is no longer present, even if the amplitude coefficients are statistically independent of each other.
- While for equally probable ternary symbols
- the entropy is $H = {\rm log}_2(3) = 1.585 \ {\rm bit/ternary \ symbol}$
- from which the equivalent bit rate can be calculated according to $R_{\rm B} = H/T$,
- here applies with probabilities $p_0 = 0.2$ and $p_{–} = p_+ = 0.4$:
- $$H \ = \ 0.2 \cdot {\rm log_2} (5) + 2 \cdot 0.4 \cdot {\rm log_2} (2.5)= 0.2 \cdot 2.322 + 0.8 \cdot 1.322 \hspace{0.15cm}\underline {\approx 1.522\,\, {\rm bit/ternary \ symbol}} \hspace{0.05cm}.$$
- Thus, the equivalent bit rate here is $\approx 4 \ \%$ smaller than the maximum possible equivalent bit rate for $M = 3$.