Difference between revisions of "Channel Coding/Distance Characteristics and Error Probability Bounds"
| (88 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Convolutional Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Decoding of Convolutional Codes |
| − | |Nächste Seite= | + | |Nächste Seite=Soft-in Soft-Out Decoder |
}} | }} | ||
| − | == | + | == Free distance vs. minimum distance == |
<br> | <br> | ||
| − | + | An important parameter regarding the error probability of linear block codes is the "minimum distance" between two code words $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$: | |
| − | :<math>d_{\rm min}(\mathcal{C}) = | + | ::<math>d_{\rm min}(\mathcal{C}) = |
| − | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') |
= | = | ||
\min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *The second part of the equation arises from the fact that every linear code also includes the zero word ⇒ $(\underline{0})$. | |
| − | {{ | + | *It is therefore convenient to set $\underline{x}\hspace{0.05cm}' = \underline{0}$, so that the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding| $\text{Hamming distance}$]] $d_{\rm H}(\underline{x}, \ \underline{0})$ gives the same result as the Hamming weight $w_{\rm H}(\underline{x})$.<br> |
| − | |||
| − | + | {{GraueBox|TEXT= | |
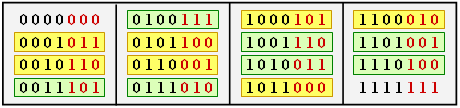
| + | $\text{Example 1:}$ The table shows the $16$ code words of of an exemplary [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|$\text{HC (7, 4, 3)}$]] $($see $\text{Examples 6 and 7})$.<br> | ||
| + | [[File:P ID2684 KC T 3 5 S1 neu.png|right|frame| Code words of the considered $(7, 4, 3)$ Hamming code|class=fit]] | ||
| − | + | You can see: | |
| + | *All code words except the null word $(\underline{0})$ contain at least three ones ⇒ $d_{\rm min} = 3$. | ||
| + | |||
| + | *There are | ||
| + | :#seven code words with three "ones" $($highlighted in yellow$)$, | ||
| + | :#seven with four "ones" $($highlighted in green$)$, and | ||
| + | :#one each with no "ones" and seven "ones".}} | ||
| + | <br clear=all> | ||
| − | :<math>d_{\rm F}(\mathcal{CC}) = | + | The »<b>free distance</b>« $d_{\rm F}$ of a convolutional code $(\mathcal{CC})$ is formulaically no different from the minimum distance of a linear block code: |
| − | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | + | |
| + | ::<math>d_{\rm F}(\mathcal{CC}) = | ||
| + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') | ||
= | = | ||
\min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | In | + | [[File:P ID2685 KC T 3 5 S1c v1.png|right|frame| Some paths wih $w(\underline{x}) = d_{\rm F} = 5$|class=fit]] |
| − | * | + | In the literature instead of "$d_{\rm F}$" sometimes is also used "$d_{∞}$". |
| + | |||
| + | The graph shows three of the infinite paths with the minimum Hamming weight $w_{\rm H, \ min}(\underline{x}) = d_{\rm F} = 5$.<br> | ||
| + | |||
| + | *Major difference to the minimal distance $d_{\rm min}$ of other codes is | ||
| + | :#that in convolutional codes not information words and code words are to be considered, | ||
| + | :#but sequences with the property [[Channel_Coding/Basics_of_Convolutional_Coding#Requirements_and_definitions| »$\text{semi–infinite}$«]]. | ||
| + | |||
| + | *Each encoded sequence $\underline{x}$ describes a path through the trellis. | ||
| + | |||
| + | *The "free distance" is the smallest possible Hamming weight of such a path $($except for the zero path$)$.<br> | ||
| − | |||
| − | |||
| − | |||
| − | == | + | == Path weighting enumerator function== |
<br> | <br> | ||
| − | + | For any linear block code, a weight enumerator function can be given in a simple way because of the finite number of code words $\underline{x}$. | |
| − | + | For the [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Free_distance_vs._minimum_distance|$\text{Example 1}$]] in the previous section this is: | |
| − | + | ::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.</math> | |
| − | + | [[File:P ID2686 KC T 3 5 S2a v1.png|right|frame|Some paths and their path weightings|class=fit]] | |
| − | + | In the case of a $($non-terminated$)$ convolutional code, no such weight function can be given, since there are infinitely many, infinitely long encoded sequences $\underline{x}$ and thus also infinitely many trellis paths. | |
| − | + | To get a grip on this problem, we now assume the following: | |
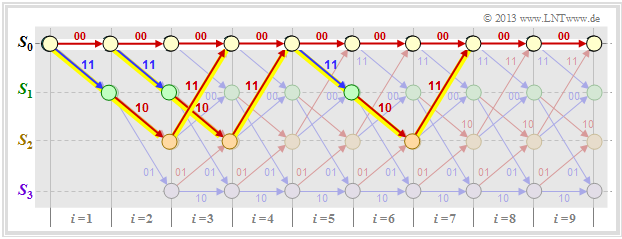
| + | *As a reference for the trellis diagram, we always choose the path of the encoded sequence $\underline{x} = \underline{0}$ and call this the "zero path" $\varphi_0$.<br> | ||
| − | + | *We now consider only paths $\varphi_j ∈ {\it \Phi}$ that all deviate from the zero path at a given time $t$ and return to it at some point later.<br> | |
| − | + | *Although only a fraction of all paths belong to the set ${\it \Phi}$, contains the remainder quantity ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} \}$ still an unbounded set of paths $\varphi_0$ is not one of them.<br> | |
| − | |||
| − | |||
| − | * | + | In the above trellis some paths $\varphi_j ∈ {\it \Phi}$ are drawn: |
| + | *The yellow path $\varphi_1$ belongs to the sequence $\underline{x}_1 = (11, 10, 11)$ with Hamming weight $w_{\rm H}(\underline{x}_1) = 5$. Thus, the path weighting $w(\varphi_1) = 5$. Due to the definition of the branching time $t$ only this single path $\varphi_1$ has the free distance $d_{\rm F} = 5$ to the zero path ⇒ $A_5 = 1$.<br> | ||
| − | + | *For the two green paths with corresponding sequences $\underline{x}_2 = (11, 01, 01, 11)$ resp. $\underline{x}_3 = (11, 10, 00, 10, 11)$ ⇒ $w(\varphi_2) = w(\varphi_3) = 6$. No other path exhibits the path weighting $6$. We take this fact into account by the coefficient $A_6 = 2$.<br> | |
| − | :<math>T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + ... \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ ... \hspace{0.1cm} | + | *Also drawn is the gray path $\varphi_4$, associated with the sequence $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Also, the sequences $\underline{x}_5 = (11, 01, 01, 00, 10, 11)$, $\underline{x}_6 = (11, 10, 00, 01, 01, 11)$ and $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$ have the same path weighting "$7$" ⇒ $A_7 = 4$.<br><br> |
| + | |||
| + | Thus, the path weighting enumerator function is for this example: | ||
| + | |||
| + | ::<math>T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | The definition of this function $T(X)$ follows.<br> | |
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ For the »<b>path weighting enumerator function</b>« of a convolutional code holds: | |
| − | |||
| − | :<math>T(X) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w = d_{\rm F}}^{\infty}\hspace{0.1cm} A_w \cdot X^w | + | ::<math>T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | # ${\it \Phi}$ denotes the set of all paths that leave the zero path $\varphi_0$ exactly at the specified time $t$ and return to it $($sometime$)$ later.<br> | |
| + | # According to the second equation part, the summands are ordered by their path weightings $w$ where $A_w$ denotes the number of paths with weighting $w$. | ||
| + | # The sum starts with $w = d_{\rm F}$.<br> | ||
| + | # The path weighting $w(\varphi_j)$ is equal to the Hamming weight $($number of "ones"$)$ of the encoded sequence $\underline{x}_j$ associated to the path $\varphi_j$: $w({\varphi_j) = w_{\rm H}(\underline {x} }_j) \hspace{0.05cm}.$}} | ||
| − | |||
| − | + | <u>Note:</u> The weight enumerator function $W(X)$ defined for linear block codes and the path weight function $T(X)$ of convolutional codes have many similarities; however, they are not identical. We consider again | |
| + | *the weight enumerator function of the $(7, 4, 3)$ Hamming code: | ||
| − | ::<math> | + | ::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},</math> |
| − | |||
| − | + | * and the path weighting enumerator function of our "standard convolutional encoder": | |
| − | |||
| − | + | ::<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} </math> | |
| − | : | + | # Noticeable is the "$1$" in the first equation, which is missing in the second one. That is: |
| + | # For the linear block codes, the reference code word $\underline{x}_i = \underline{0}$ is counted. | ||
| + | # But the zero encoded sequence $\underline{x}_i = \underline{0}$ and the zero path $\varphi_0$ are excluded by definition for convolutional codes. | ||
| − | |||
| − | : | + | {{GraueBox|TEXT= |
| + | $\text{Author's personal opinion:}$ | ||
| + | |||
| + | One could have defined $W(X)$ without the "$1$" as well. This would have avoided among other things, that the Bhattacharyya–bound for linear block codes and that for convolutional codes differ by "$-1$", as can be seen from the following equations:<br> | ||
| − | + | *[[Channel_Coding/Bounds_for_Block_Error_Probability#The_upper_bound_according_to_Bhattacharyya| "Bhattacharyya bound for $\text{linear block codes}$"]]: ${\rm Pr(block\:error)} \le W(X = \beta) -1 | |
| + | \hspace{0.05cm},$ | ||
| − | [[ | + | *[[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Burst_error_probability_and_Bhattacharyya_bound| "Bhattacharyya bound for $\text{convolutional codes}$"]]: ${\rm Pr(burst\:error)} \le T(X = \beta) |
| + | \hspace{0.05cm}.$}} | ||
| − | |||
| − | |||
| − | + | == Enhanced path weighting enumerator function == | |
| + | <br> | ||
| + | The path weighting enumerator function $T(X)$ only provides information regarding the weights of the encoded sequence $\underline{x}$. | ||
| + | *More information is obtained if the weights of the information sequence $\underline{u}$ are also collected. | ||
| + | |||
| + | *One then needs two formal parameters $X$ and $U$, as can be seen from the following definition.<br> | ||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ The »<b>enhanced path weight enumerator function</b>« $\rm (EPWEF)$ is: | ||
| − | + | ::<math>T_{\rm enh}(X,\ U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} | |
| − | |||
| − | |||
| − | |||
| − | :<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | All specifications for the $T(X)$ definition in the last section apply. In addition, note: | |
| − | + | # The path input weight $u(\varphi_j)$ is equal to the Hamming weight of the information sequence $\underline{u}_j$ associated to the path. | |
| + | # It is expressed as a power of the formal parameter $U$ .<br> | ||
| + | # $A_{w, \ u}$ denotes the number of paths $\varphi_j$ with path output weight $w(\varphi_j)$ and path input weight $u(\varphi_j)$. Control variable for the second portion is $u$.<br> | ||
| + | # Setting the formal parameter $U = 1$ in the enhanced path weighting enumerator function yields the original weighting enumerator function $T(X)$.<br> | ||
| − | |||
| − | + | For many $($and all relevant$)$ convolutional codes, upper equation can still be simplified: | |
| − | + | ::<math>T_{\rm enh}(X,\ U) =\hspace{0.1cm} \sum_{w \ = \ d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} | |
| + | \hspace{0.05cm}.</math>}}<br> | ||
| − | + | {{GraueBox|TEXT= | |
| − | \ | + | $\text{Example 2:}$ Thus, the enhanced path weighting enumerator function of our standard encoder is: |
| − | + | ::<math>T_{\rm enh}(X,\ U) = U \cdot X^5 + 2 \cdot U^2 \cdot X^6 + 4 \cdot U^3 \cdot X^7+ \text{ ...} \hspace{0.1cm} | |
| + | \hspace{0.05cm}.</math> | ||
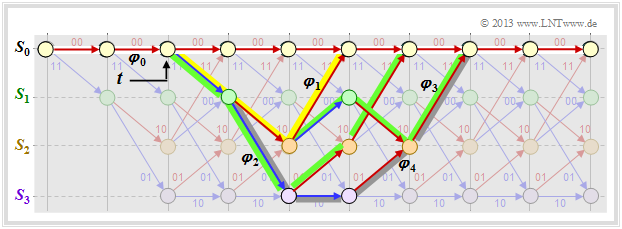
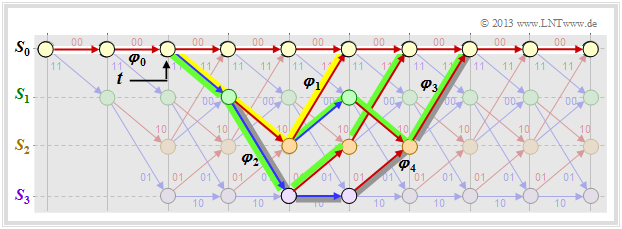
| − | : | + | [[File:P ID2702 KC T 3 5 S2a v1.png|right|frame|Some paths and their path weightings|class=fit]] |
| − | + | Comparing this result with the trellis shown below, we can see: | |
| + | *The yellow highlighted path – in $T(X)$ marked by $X^5$ – is composed of a blue arrow $(u_i = 1)$ and two red arrows $(u_i = 0)$. Thus $X^5$ becomes the extended term $U X^5$.<br> | ||
| − | + | *The sequences of the two green paths are | |
| − | * | + | :$$\underline{u}_2 = (1, 1, 0, 0) \hspace{0.15cm} ⇒ \hspace{0.15cm} \underline{x}_2 = (11, 01, 01, 11),$$ |
| + | :$$\underline{u}_3 = (1, 0, 1, 0, 0) \hspace{0.15cm} ⇒ \hspace{0.15cm} \underline{x}_3 = (11, 10, 00, 10, 11).$$ | ||
| + | :This gives the second term $2 \cdot U^2X^6$.<br> | ||
| − | * | + | *The gray path $($and the three undrawn paths$)$ together make the contribution $4 \cdot U^3X^7$. Each of these paths contains three blue arrows ⇒ three "ones" in the associated information sequence.<br>}} |
| − | |||
| − | |||
| − | == | + | == Path weighting enumerator function from state transition diagram == |
<br> | <br> | ||
| − | + | There is an elegant way to determine the path weighting enumerator function $T(X)$ and its enhancement directly from the state transition diagram. This will be demonstrated here and in the following sections using our [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#State_definition_for_a_memory_register|$\text{standard convolutional encoder}$]] as an example.<br> | |
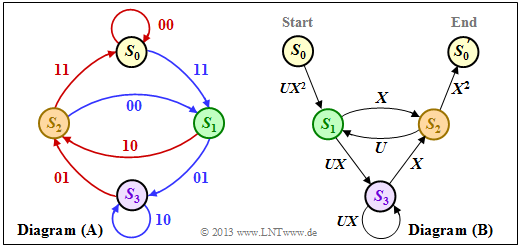
| − | + | First, the state transition diagram must be redrawn for this purpose. The graphic shows this on the left in the previous form as diagram $\rm (A)$, while the new diagram $\rm (B)$ is given on the right. It can be seen: | |
| − | [[File: | + | [[File:KC_T_3_5_Diagram_v3.png|right|frame|State transition diagram in two different variants|class=fit]] |
| − | + | # The state $S_0$ is split into the start state $S_0$ and the end state $S_0\hspace{0.01cm}'$. Thus, all paths of the trellis that start in state $S_0$ and return to it at some point can also be traced in the right graph $\rm (B)$. Excluded are direct transitions from $S_0$ to $S_0\hspace{0.01cm}'$ and thus also the zero path.<br> | |
| − | + | # In diagram $\rm (A)$ the transitions are distinguishable by the colors red $($for $u_i = 0)$ and blue $($for $u_i = 1)$. | |
| + | # The code words $\underline{x}_i ∈ \{00, 01, 10, 11\}$ are noted at the transitions. In diagram $\rm (B)$ $(00)$ is expressed by $X^0 = 1$ and $(11)$ by $X^2$. | ||
| + | # The code words $(01)$ and $(10)$ are now indistinguishable, but they are uniformly denoted by $X$ .<br> | ||
| + | # Phrased another way: The code word $\underline{x}_i$ is now represented as $X^w$ where $X$ is a dummy variable associated with the output. | ||
| + | # $w = w_{\rm H}(\underline{x}_i)$ indicates the Hamming weight of the code word $\underline{x}_i$. For a rate $1/2$ code, the exponent $w$ is either $0, \ 1$ or $2$.<br> | ||
| + | # Also diagram $\rm (B)$ omits the color coding. The information bit $u_i = 1$ is now denoted by $U^1 = U$ and bit $u_i = 0$ by $U^0 = 1$. The dummy variable $U$ is thus assigned to the input sequence $\underline{u}$ .<br> | ||
| + | |||
| + | == Rules for manipulating the state transition diagram == | ||
| + | <br> | ||
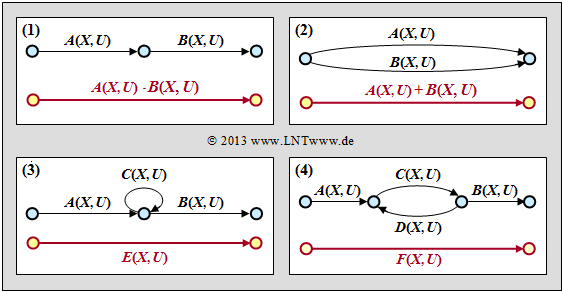
| + | Goal of our calculations will be to characterize the $($arbitrarily complicated$)$ path from $S_0$ to $S_0\hspace{0.01cm}'$ by the extended path weighting enumerator function $T_{\rm enh}(X, \ U)$. For this we need rules to simplify the graph stepwise.<br> | ||
| − | + | »'''Serial transitions'''« | |
| + | [[File:KC_T_3_5_Einzelteile_neu.png|right|frame|Reduction of serial transitions '''(1)''', parallel transitions '''(2)''', a ring | ||
| + | '''(3)''', a feedback '''(4)''' ]] | ||
| − | + | Two serial connections – denoted by $A(X, \ U)$ and $B(X, \ U)$ – can be replaced by a single connection with the product of these ratings.<br> | |
| − | + | »'''Parallel transitions'''« | |
| − | + | Two parallel connections – denoted by $A(X, \ U)$ and $B(X, \ U)$ – are combined by the sum of their valuation functions.<br> | |
| − | + | »'''Ring'''« | |
| − | |||
| − | |||
| − | + | The adjacent constellation can be replaced by a single connection, and the following applies to the replacement: | |
| − | + | ::<math>E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} | |
| − | + | \hspace{0.05cm}.</math> | |
| − | |||
| − | + | »'''Feedback'''« | |
| − | + | Due to the feedback, two states can alternate here as often as desired. For this constellation applies: | |
| + | ::<math>F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} | ||
| + | \hspace{0.05cm}.</math> | ||
| − | + | The equations for ring and feedback given here are to be proved in the [[Aufgaben:Exercise_3.12Z:_Ring_and_Feedback|"Exercise 3.12Z"]] . | |
| − | + | <br clear=all> | |
| − | + | {{GraueBox|TEXT= | |
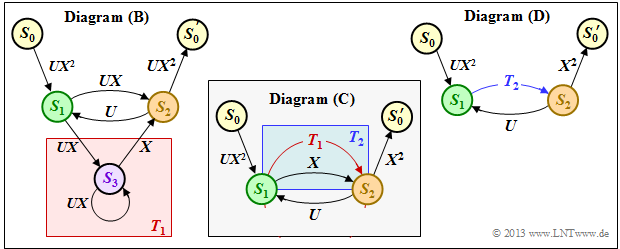
| + | $\text{Example 3:}$ | ||
| + | The above rules are now to be applied to our standard example. In the graphic on the left you can see the modified diagram $\rm (B)$. | ||
| − | + | [[File:EN_KC_T_3_5_S48.png|right|frame|Reduction of state transitions|class=fit]] | |
| − | |||
| − | + | *First we replace the red highlighted detour from $S_1$ to $S_2$ via $S_3$ in the diagram $\rm (B)$ by the red connection $T_1(X, \hspace{0.05cm} U)$ drawn in the diagram $\rm (C)$. | |
| − | \hspace{0.05cm}. | ||
| − | + | *According to the upper classification, it is a "ring" with the labels $A = C = U \cdot X$ and $B = X$, and we obtain for the first reduction function: | |
| − | |||
| − | :<math> | + | ::<math>T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *Now we summarize the parallel connections according to the blue background in the diagram $\rm (C)$ and replace it with the blue connection in the diagram $\rm (D)$. The second reduction function is thus: | |
| − | + | :$$T_2(X, \hspace{0.03cm}U) = T_1(X, \hspace{0.03cm}U) \hspace{-0.03cm}+\hspace{-0.03cm} X\hspace{-0.03cm} $$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm} T_2(X, \hspace{0.05cm}U) =\hspace{-0.03cm} \frac{U X^2\hspace{-0.03cm} +\hspace{-0.03cm} X \cdot (1-UX)}{1- U X}= \frac{X}{1- U X}\hspace{0.05cm}.$$ | |
| − | + | ||
| − | + | *The entire graph $\rm (D)$ can then be replaced by a single connection from $S_0$ to $S_0\hspace{0.01cm}'$. According to the feedback rule, one obtains for the "enhanced path weighting enumerator function": | |
| − | ::<math> | + | ::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *With the series expansion $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $ can also be written for this purpose: |
| − | ::<math> | + | ::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \big [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + \text{...} \hspace{0.05cm} \big ] |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Setting the formal input variable $U = 1$, we obtain the "simple path weighting enumerator function", which alone allows statements about the weighting distribution of the output sequence $\underline{x}$: |
| − | ::<math> | + | ::<math>T(X) = X^5 \cdot \big [ 1 + 2 X + 4 X^2 + 8 X^3 +\text{...}\hspace{0.05cm} \big ] |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | We have already read the same result from the trellis diagram in section [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Path_weighting_enumerator_function| "Path weighting enumerator function"]] . There was | |
| + | **one gray path with weight $5$, | ||
| + | **two yellow paths with weighting $6$ | ||
| + | ** four green paths with weighting $7$ | ||
| + | ** and ... .}}<br> | ||
| − | + | == Block error probability vs. burst error probability == | |
| − | + | <br> | |
| + | The simple model according to the sketch is valid for linear block codes as well as for convolutional codes.<br> | ||
| + | |||
| + | [[File:EN_KC_T_3_5_S5.png|right|frame|Simple transmission model including encoding and decoding|class=fit]] | ||
| − | |||
| − | + | »'''Block codes'''« | |
| − | + | For block codes denote $\underline{u} = (u_1, \ \text{...} \hspace{0.05cm}, \ u_i, \ \text{...} \hspace{0.05cm}, \ u_k)$ and $\underline{v} = (v_1, \ \text{...} \hspace{0.05cm}, v_i, \ \text{...} \hspace{0.05cm} \ , \ v_k)$ the information blocks at the input and output of the system. | |
| − | \hspace{0.05cm}. | ||
| − | + | Thus, the following descriptive variables can be specified: | |
| + | *the »block error probability« ${\rm Pr(block\:error)} = {\rm Pr}(\underline{v} ≠ \underline{u}),$ | ||
| − | = | + | *the »bit error probability« ${\rm Pr(bit\:error)} = {\rm Pr}(v_i ≠ u_i).$<br><br> |
| − | <br> | ||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Please note:}$ In real transmission systems, due to thermal noise the following always applies: | ||
| + | :$${\rm Pr(bit\:error)} > 0\hspace{0.05cm},\hspace{0.5cm}{\rm Pr(block\:error)} > {\rm Pr(bit\:error)} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | For this a simple explanation attempt: If the decoder decides in each block of length $k$ exactly one bit wrong, | |
| − | * | + | *so the average bit error probability ${\rm Pr(bit\:error)}= 1/k$, |
| − | * | + | *while for the block error probability ${\rm Pr(block\:error)}\equiv 1$ holds.}}<br> |
| − | |||
| − | + | »'''Convolutional codes'''« | |
| − | |||
| − | + | For convolutional codes, the block error probability cannot be specified, since here $\underline{u} = (u_1, \ u_2, \ \text{...} \hspace{0.05cm})$ and $\underline{\upsilon} = (v_1, \ v_2, \ \text{...} \hspace{0.05cm})$ represent sequences. | |
| − | + | [[File:P ID2706 KC T 3 5 S5b v1.png|right|frame|Zero path ${\it \varphi}_0$ and deviation paths ${\it \varphi}_i$|class=fit]] | |
| − | + | <br><br>Even the smallest possible code parameter $k = 1$, leads here to the sequence length $k \hspace{0.05cm}' → ∞$, and | |
| + | * the block error probability would always result in ${\rm Pr(block\hspace{0.1cm} error)}\equiv 1$, | ||
| − | + | *even if the bit error probability is extremely small $\hspace{0.05cm}$ $($but non-zero$)$. | |
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ For the »<b>burst error probability</b> « of a convolutional code holds: | ||
| − | :<math>{\rm Pr( | + | ::<math>{\rm Pr(burst\:error)} = {\rm Pr}\big \{ {\rm Decoder\hspace{0.15cm} leaves\hspace{0.15cm} the\hspace{0.15cm} correct\hspace{0.15cm}path}\hspace{0.15cm}{\rm at\hspace{0.15cm}time \hspace{0.10cm}\it t}\big \} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *To simplify the notation for the following derivation, we always assume the zero sequence $\underline{0}$ which is shown in red in the drawn trellis as the "zero path" $\varphi_0$. | |
| + | |||
| + | *All other paths $\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} $ $($and many more$)$ leave $\varphi_0$ at time $t$. | ||
| + | |||
| + | *They all belong to the path set ${\it \Phi}$ which is defined as "Viterbi decoder leaves the correct path at time $t$". This probability is calculated in the next section.}}<br> | ||
| − | == | + | == Burst error probability and Bhattacharyya bound == |
<br> | <br> | ||
| − | + | [[File:EN_KC_T_3_5_S5c.png|right|frame|Calculation of the burst error probability|class=fit]] | |
| + | We proceed as in the earlier chapter [[Channel_Coding/Bounds_for_Block_Error_Probability#Union_Bound_of_the_block_error_probability|"Bounds for block error probability"]] | ||
| + | *from the pairwise error probability ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ | ||
| + | |||
| + | *that instead of the path $\varphi_0$ | ||
| + | |||
| + | *the decoder <b>could</b> select the path $\varphi_i$. | ||
| − | |||
| − | + | All considered paths $\varphi_i$ leave the zero path $\varphi_0$ at time $t$; thus they all belong to the path set ${\it \Phi}$.<br> | |
| − | : | + | The sought "burst error probability" is equal to the following union set: |
| − | + | :$${\rm Pr(burst\:error)}= {\rm Pr}\left (\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}\big] \hspace{0.05cm}\cup\hspace{0.05cm}\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}\big]\hspace{0.05cm}\cup\hspace{0.05cm} \text{... }\hspace{0.05cm} \right )$$ | |
| + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr(burst\:error)}= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} \big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big] \right )\hspace{0.05cm}.$$ | ||
| − | :<math>{\rm Pr( | + | *An upper bound for this is provided by the so-called [[Channel_Coding/Bounds_for_Block_Error_Probability#Union_Bound_of_the_block_error_probability|$\text{Union Bound}$]]: |
| − | {\rm Pr}\ | + | |
| + | ::<math>{\rm Pr(Burst\:error)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} | ||
| + | {\rm Pr}\big [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big ] = {\rm Pr(union \hspace{0.15cm}bound)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *The pairwise error probability can be estimated using the [[Channel_Coding/Bounds_for_Block_Error_Probability#The_upper_bound_according_to_Bhattacharyya|$\text{Bhattacharyya bound}$]]: | |
| − | :<math>{\rm Pr}\ | + | ::<math>{\rm Pr}\big [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\big ] |
\le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] | {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] | ||
| Line 279: | Line 339: | ||
\hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.</math> | \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.</math> | ||
| − | + | :Here denotes | |
| + | |||
| + | :*$w_{\rm H}(\underline{x}_i)$ is the Hamming weight of the possible encoded sequence $\underline{x}_i,$ | ||
| + | |||
| + | :*$\ w(\varphi_i)$ is the path weight of the corresponding path $\varphi_i ∈ {\it \Phi},$ | ||
| + | |||
| + | :*$\beta$ is the so-called [[Channel_Coding/Bounds_for_Block_Error_Probability#The_upper_bound_according_to_Bhattacharyya|$\text{Bhattacharyya parameter}$]].<br> | ||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | T(X) | + | By »'''summing over all paths'''« and comparing with the (simple) [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Path_weighting_enumerator_function|$\text{path weighting function}$]] $T(X)$ we get the result: |
| − | |||
| − | + | ::<math>{\rm Pr(burst\:error)} \le T(X = \beta),\hspace{0.5cm}{\rm with}\hspace{0.5cm} | |
| + | T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi} }\hspace{0.15cm} | ||
| + | \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.</math>}} | ||
| − | :<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + ... \hspace{0.1cm} | + | |
| − | = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ ... \hspace{0.1cm}) | + | {{GraueBox|TEXT= |
| + | $\text{Example 4: }$ For our standard encoder with | ||
| + | * code rate $R = 1/2$, | ||
| + | |||
| + | *memory $m = 2$, | ||
| + | |||
| + | * D– transfer function $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D)$, | ||
| + | |||
| + | |||
| + | we have obtained the following [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Path_weighting_enumerator_function|$\text{path weighting enumerator function}$]]: | ||
| + | |||
| + | ::<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + \ \text{...} \hspace{0.1cm} | ||
| + | = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ \ \text{...} \hspace{0.1cm}) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \hspace{0.15cm} $ can also be written for this purpose: | |
| − | :<math>T(X) = \frac{X^5}{1-2 \cdot X} | + | ::<math>T(X) = \frac{X^5}{1-2 \cdot X} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *The BSC model provides the following Bhattacharyya bound with the falsification probability $\varepsilon$: | |
| − | :<math>{\rm Pr( | + | ::<math>{\rm Pr(Burst\:error)} \le T(X = \beta) = T\big ( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)} \big ) |
= \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.</math> | = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.</math> | ||
| + | *In the [[Aufgaben:Exercise_3.14:_Error_Probability_Bounds|"Exercise 3.14"]] this equation is to be evaluated numerically.}}<br> | ||
| + | |||
| + | == Bit error probability and Viterbi bound == | ||
| + | <br> | ||
| + | Finally, an upper bound is given for the bit error probability. According to the graph, we proceed as in [Liv10]<ref name='Liv10'>Liva, G.: Channel Coding. Lecture manuscript, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.</ref> assume the following conditions:<br> | ||
| − | + | *The zero sequence $\underline{x} = \underline{0}$ was sent ⇒ Path $\varphi_0$.<br> | |
| − | + | *The duration of a path deviation $($"error burst duration"$)$ is denoted by $L$ .<br> | |
| − | |||
| − | |||
| − | + | *The distance between two bursts $($"inter burst time"$)$ we call $N$.<br> | |
| − | * | + | *The Hamming weight of the error bundle be $H$.<br> |
| − | |||
| − | |||
| − | + | For a rate $1/n$ convolutional code ⇒ $k = 1$ ⇒ one information bit per clock, the expected values ${\rm E}\big[L \big]$, ${\rm E}\big[N \big]$ and ${\rm E}\big[H\big]$ of the random variables defined above to give an upper bound for the bit error probability: | |
| − | + | [[File:P ID2715 KC T 3 5 S6a v1.png|right|frame|For the definition of the description variables $L$, $N$ and $H$|class=fit]] | |
| − | :<math>{\rm Pr( | + | ::<math>{\rm Pr(bit\:error)} = \frac{{\rm E}\big[H\big]}{{\rm E}[L] + {\rm E}\big[N\big]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}\big[H\big]}{{\rm E}\big[N\big]} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | It is assumed that | |
| + | # the (mean) duration of an error burst is in practice much smaller than the expected distance between two bursts, | ||
| + | # the (mean) inter burst time $E\big[N\big]$ is equal to the inverse of the burst error probability, | ||
| + | # the expected value in the numerator is estimated as follows: | ||
| − | :<math>{\rm E}[H] \le \frac{1}{\rm Pr( | + | ::<math>{\rm E}\big[H \big] \le \frac{1}{\rm Pr(burst\:error)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} |
\hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} | \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | In deriving this bound, the "pairwise error probability" ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ and the "Bhattacharyya estimation" are used. Thus we obtain with | |
| − | * | + | *the path input weighting $u(\varphi_i),$ |
| + | |||
| + | *the path output weighting $w(\varphi_i),$ and | ||
| − | * | + | *the Bhattacharyya parameter $\beta$ |
| − | |||
| − | + | the following estimation for the bit error probability and refer to it as the »<b>Viterbi bound</b>«: | |
| − | :<math>{\rm Pr( | + | ::<math>{\rm Pr(bit\:error)}\le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} |
| − | \hspace{0. | + | \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | This intermediate result can also be represented in another form. We recall the [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Enhanced_path_weighting_enumerator_function|$\text{enhanced path weighting enumerator function}$]] | ||
| − | + | ::<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} | |
| + | \hspace{0.05cm}.</math> | ||
| − | + | If we derive this function according to the dummy input variable $U$, we get | |
| − | |||
| − | |||
| − | :<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} | + | ::<math>\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Finally, if we set $U = 1$ for the dummy input variable, than we see the connection to the above result: | |
| − | :<math>\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \ | + | ::<math>\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.</math> |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Conclusion:}$ The »<b>bit error probability</b>« of a convolutional code can be estimated using the extended path weighting enumerator function in closed form: | ||
| + | ::<math>{\rm Pr(bit\:error)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{ {\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1} } | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *One speaks of the »<b>Viterbi bound</b>». Here one derives the enhanced path weighting enumerator function after the second parameter $U$ and then sets | |
| + | ::$$X = \beta,\hspace{0.4cm} U = 1.$$}}<br> | ||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 5:}$ The graph illustrates the good correction capability ⇒ small bit error rate $\rm (BER)$ of convolutional codes at the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\text{$\rm AWGN$ channel}$]]. | ||
| + | [[File:EN_KC_T_3_5_S6.png|right|frame|AWGN bit error probability of convolutional codes]] | ||
| + | |||
| + | *Red circles denote the $\rm BER$ for our "rate $1/2$ standard encoder" with memory $m = 2$.<br> | ||
| − | |||
| − | + | *Green crosses mark a convolutional code with $m = 6$, the so-called [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance|$\text{industry standard code}$]].<br> | |
| − | |||
| − | |||
| − | + | * Codes with large memory $m$ lead to large gains over uncoded transmission. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br><br><br><br> | |
| + | <u>Note:</u> | ||
| − | == | + | In [[Aufgaben:Exercise_3.14:_Error_Probability_Bounds|"Exercise 3.14"]], the "Viterbi bound" and the "Bhattacharyya bound" are evaluated numerically for the "rate $1/2$ standard encoder" and the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC model}$]]. |
| + | }} | ||
| + | |||
| + | |||
| + | == Exercises for the chapter == | ||
<br> | <br> | ||
| − | [[Aufgaben:3.12 | + | [[Aufgaben:Exercise_3.12:_Path_Weighting_Function|Exercise 3.12: Path Weighting Function]] |
| + | |||
| + | [[Aufgaben:Exercise_3.12Z:_Ring_and_Feedback|Exercise 3.12Z: Ring and Feedback]] | ||
| − | [[ | + | [[Aufgaben:Exercise_3.13:_Path_Weighting_Function_again|Exercise 3.13: Path Weighting Function again]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.14:_Error_Probability_Bounds|Exercise 3.14: Error Probability Bounds]] |
| − | + | ==References== | |
| + | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 18:24, 20 December 2022
Contents
- 1 Free distance vs. minimum distance
- 2 Path weighting enumerator function
- 3 Enhanced path weighting enumerator function
- 4 Path weighting enumerator function from state transition diagram
- 5 Rules for manipulating the state transition diagram
- 6 Block error probability vs. burst error probability
- 7 Burst error probability and Bhattacharyya bound
- 8 Bit error probability and Viterbi bound
- 9 Exercises for the chapter
- 10 References
Free distance vs. minimum distance
An important parameter regarding the error probability of linear block codes is the "minimum distance" between two code words $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
- The second part of the equation arises from the fact that every linear code also includes the zero word ⇒ $(\underline{0})$.
- It is therefore convenient to set $\underline{x}\hspace{0.05cm}' = \underline{0}$, so that the $\text{Hamming distance}$ $d_{\rm H}(\underline{x}, \ \underline{0})$ gives the same result as the Hamming weight $w_{\rm H}(\underline{x})$.
$\text{Example 1:}$ The table shows the $16$ code words of of an exemplary $\text{HC (7, 4, 3)}$ $($see $\text{Examples 6 and 7})$.
You can see:
- All code words except the null word $(\underline{0})$ contain at least three ones ⇒ $d_{\rm min} = 3$.
- There are
- seven code words with three "ones" $($highlighted in yellow$)$,
- seven with four "ones" $($highlighted in green$)$, and
- one each with no "ones" and seven "ones".
The »free distance« $d_{\rm F}$ of a convolutional code $(\mathcal{CC})$ is formulaically no different from the minimum distance of a linear block code:
- \[d_{\rm F}(\mathcal{CC}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
In the literature instead of "$d_{\rm F}$" sometimes is also used "$d_{∞}$".
The graph shows three of the infinite paths with the minimum Hamming weight $w_{\rm H, \ min}(\underline{x}) = d_{\rm F} = 5$.
- Major difference to the minimal distance $d_{\rm min}$ of other codes is
- that in convolutional codes not information words and code words are to be considered,
- but sequences with the property »$\text{semi–infinite}$«.
- Each encoded sequence $\underline{x}$ describes a path through the trellis.
- The "free distance" is the smallest possible Hamming weight of such a path $($except for the zero path$)$.
Path weighting enumerator function
For any linear block code, a weight enumerator function can be given in a simple way because of the finite number of code words $\underline{x}$.
For the $\text{Example 1}$ in the previous section this is:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
In the case of a $($non-terminated$)$ convolutional code, no such weight function can be given, since there are infinitely many, infinitely long encoded sequences $\underline{x}$ and thus also infinitely many trellis paths.
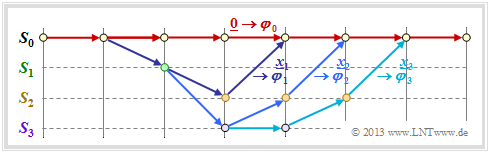
To get a grip on this problem, we now assume the following:
- As a reference for the trellis diagram, we always choose the path of the encoded sequence $\underline{x} = \underline{0}$ and call this the "zero path" $\varphi_0$.
- We now consider only paths $\varphi_j ∈ {\it \Phi}$ that all deviate from the zero path at a given time $t$ and return to it at some point later.
- Although only a fraction of all paths belong to the set ${\it \Phi}$, contains the remainder quantity ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} \}$ still an unbounded set of paths $\varphi_0$ is not one of them.
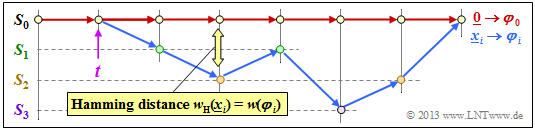
In the above trellis some paths $\varphi_j ∈ {\it \Phi}$ are drawn:
- The yellow path $\varphi_1$ belongs to the sequence $\underline{x}_1 = (11, 10, 11)$ with Hamming weight $w_{\rm H}(\underline{x}_1) = 5$. Thus, the path weighting $w(\varphi_1) = 5$. Due to the definition of the branching time $t$ only this single path $\varphi_1$ has the free distance $d_{\rm F} = 5$ to the zero path ⇒ $A_5 = 1$.
- For the two green paths with corresponding sequences $\underline{x}_2 = (11, 01, 01, 11)$ resp. $\underline{x}_3 = (11, 10, 00, 10, 11)$ ⇒ $w(\varphi_2) = w(\varphi_3) = 6$. No other path exhibits the path weighting $6$. We take this fact into account by the coefficient $A_6 = 2$.
- Also drawn is the gray path $\varphi_4$, associated with the sequence $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Also, the sequences $\underline{x}_5 = (11, 01, 01, 00, 10, 11)$, $\underline{x}_6 = (11, 10, 00, 01, 01, 11)$ and $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$ have the same path weighting "$7$" ⇒ $A_7 = 4$.
Thus, the path weighting enumerator function is for this example:
- \[T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} \hspace{0.05cm}.\]
The definition of this function $T(X)$ follows.
$\text{Definition:}$ For the »path weighting enumerator function« of a convolutional code holds:
- \[T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \hspace{0.05cm}.\]
- ${\it \Phi}$ denotes the set of all paths that leave the zero path $\varphi_0$ exactly at the specified time $t$ and return to it $($sometime$)$ later.
- According to the second equation part, the summands are ordered by their path weightings $w$ where $A_w$ denotes the number of paths with weighting $w$.
- The sum starts with $w = d_{\rm F}$.
- The path weighting $w(\varphi_j)$ is equal to the Hamming weight $($number of "ones"$)$ of the encoded sequence $\underline{x}_j$ associated to the path $\varphi_j$: $w({\varphi_j) = w_{\rm H}(\underline {x} }_j) \hspace{0.05cm}.$
Note: The weight enumerator function $W(X)$ defined for linear block codes and the path weight function $T(X)$ of convolutional codes have many similarities; however, they are not identical. We consider again
- the weight enumerator function of the $(7, 4, 3)$ Hamming code:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},\]
- and the path weighting enumerator function of our "standard convolutional encoder":
- \[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} \]
- Noticeable is the "$1$" in the first equation, which is missing in the second one. That is:
- For the linear block codes, the reference code word $\underline{x}_i = \underline{0}$ is counted.
- But the zero encoded sequence $\underline{x}_i = \underline{0}$ and the zero path $\varphi_0$ are excluded by definition for convolutional codes.
$\text{Author's personal opinion:}$
One could have defined $W(X)$ without the "$1$" as well. This would have avoided among other things, that the Bhattacharyya–bound for linear block codes and that for convolutional codes differ by "$-1$", as can be seen from the following equations:
- "Bhattacharyya bound for $\text{linear block codes}$": ${\rm Pr(block\:error)} \le W(X = \beta) -1 \hspace{0.05cm},$
- "Bhattacharyya bound for $\text{convolutional codes}$": ${\rm Pr(burst\:error)} \le T(X = \beta) \hspace{0.05cm}.$
Enhanced path weighting enumerator function
The path weighting enumerator function $T(X)$ only provides information regarding the weights of the encoded sequence $\underline{x}$.
- More information is obtained if the weights of the information sequence $\underline{u}$ are also collected.
- One then needs two formal parameters $X$ and $U$, as can be seen from the following definition.
$\text{Definition:}$ The »enhanced path weight enumerator function« $\rm (EPWEF)$ is:
- \[T_{\rm enh}(X,\ U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
All specifications for the $T(X)$ definition in the last section apply. In addition, note:
- The path input weight $u(\varphi_j)$ is equal to the Hamming weight of the information sequence $\underline{u}_j$ associated to the path.
- It is expressed as a power of the formal parameter $U$ .
- $A_{w, \ u}$ denotes the number of paths $\varphi_j$ with path output weight $w(\varphi_j)$ and path input weight $u(\varphi_j)$. Control variable for the second portion is $u$.
- Setting the formal parameter $U = 1$ in the enhanced path weighting enumerator function yields the original weighting enumerator function $T(X)$.
For many $($and all relevant$)$ convolutional codes, upper equation can still be simplified:
- \[T_{\rm enh}(X,\ U) =\hspace{0.1cm} \sum_{w \ = \ d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
$\text{Example 2:}$ Thus, the enhanced path weighting enumerator function of our standard encoder is:
- \[T_{\rm enh}(X,\ U) = U \cdot X^5 + 2 \cdot U^2 \cdot X^6 + 4 \cdot U^3 \cdot X^7+ \text{ ...} \hspace{0.1cm} \hspace{0.05cm}.\]
Comparing this result with the trellis shown below, we can see:
- The yellow highlighted path – in $T(X)$ marked by $X^5$ – is composed of a blue arrow $(u_i = 1)$ and two red arrows $(u_i = 0)$. Thus $X^5$ becomes the extended term $U X^5$.
- The sequences of the two green paths are
- $$\underline{u}_2 = (1, 1, 0, 0) \hspace{0.15cm} ⇒ \hspace{0.15cm} \underline{x}_2 = (11, 01, 01, 11),$$
- $$\underline{u}_3 = (1, 0, 1, 0, 0) \hspace{0.15cm} ⇒ \hspace{0.15cm} \underline{x}_3 = (11, 10, 00, 10, 11).$$
- This gives the second term $2 \cdot U^2X^6$.
- The gray path $($and the three undrawn paths$)$ together make the contribution $4 \cdot U^3X^7$. Each of these paths contains three blue arrows ⇒ three "ones" in the associated information sequence.
Path weighting enumerator function from state transition diagram
There is an elegant way to determine the path weighting enumerator function $T(X)$ and its enhancement directly from the state transition diagram. This will be demonstrated here and in the following sections using our $\text{standard convolutional encoder}$ as an example.
First, the state transition diagram must be redrawn for this purpose. The graphic shows this on the left in the previous form as diagram $\rm (A)$, while the new diagram $\rm (B)$ is given on the right. It can be seen:
- The state $S_0$ is split into the start state $S_0$ and the end state $S_0\hspace{0.01cm}'$. Thus, all paths of the trellis that start in state $S_0$ and return to it at some point can also be traced in the right graph $\rm (B)$. Excluded are direct transitions from $S_0$ to $S_0\hspace{0.01cm}'$ and thus also the zero path.
- In diagram $\rm (A)$ the transitions are distinguishable by the colors red $($for $u_i = 0)$ and blue $($for $u_i = 1)$.
- The code words $\underline{x}_i ∈ \{00, 01, 10, 11\}$ are noted at the transitions. In diagram $\rm (B)$ $(00)$ is expressed by $X^0 = 1$ and $(11)$ by $X^2$.
- The code words $(01)$ and $(10)$ are now indistinguishable, but they are uniformly denoted by $X$ .
- Phrased another way: The code word $\underline{x}_i$ is now represented as $X^w$ where $X$ is a dummy variable associated with the output.
- $w = w_{\rm H}(\underline{x}_i)$ indicates the Hamming weight of the code word $\underline{x}_i$. For a rate $1/2$ code, the exponent $w$ is either $0, \ 1$ or $2$.
- Also diagram $\rm (B)$ omits the color coding. The information bit $u_i = 1$ is now denoted by $U^1 = U$ and bit $u_i = 0$ by $U^0 = 1$. The dummy variable $U$ is thus assigned to the input sequence $\underline{u}$ .
Rules for manipulating the state transition diagram
Goal of our calculations will be to characterize the $($arbitrarily complicated$)$ path from $S_0$ to $S_0\hspace{0.01cm}'$ by the extended path weighting enumerator function $T_{\rm enh}(X, \ U)$. For this we need rules to simplify the graph stepwise.
»Serial transitions«
Two serial connections – denoted by $A(X, \ U)$ and $B(X, \ U)$ – can be replaced by a single connection with the product of these ratings.
»Parallel transitions«
Two parallel connections – denoted by $A(X, \ U)$ and $B(X, \ U)$ – are combined by the sum of their valuation functions.
»Ring«
The adjacent constellation can be replaced by a single connection, and the following applies to the replacement:
- \[E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.\]
»Feedback«
Due to the feedback, two states can alternate here as often as desired. For this constellation applies:
- \[F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} \hspace{0.05cm}.\]
The equations for ring and feedback given here are to be proved in the "Exercise 3.12Z" .
$\text{Example 3:}$ The above rules are now to be applied to our standard example. In the graphic on the left you can see the modified diagram $\rm (B)$.
- First we replace the red highlighted detour from $S_1$ to $S_2$ via $S_3$ in the diagram $\rm (B)$ by the red connection $T_1(X, \hspace{0.05cm} U)$ drawn in the diagram $\rm (C)$.
- According to the upper classification, it is a "ring" with the labels $A = C = U \cdot X$ and $B = X$, and we obtain for the first reduction function:
- \[T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} \hspace{0.05cm}.\]
- Now we summarize the parallel connections according to the blue background in the diagram $\rm (C)$ and replace it with the blue connection in the diagram $\rm (D)$. The second reduction function is thus:
- $$T_2(X, \hspace{0.03cm}U) = T_1(X, \hspace{0.03cm}U) \hspace{-0.03cm}+\hspace{-0.03cm} X\hspace{-0.03cm} $$
- $$\Rightarrow \hspace{0.3cm} T_2(X, \hspace{0.05cm}U) =\hspace{-0.03cm} \frac{U X^2\hspace{-0.03cm} +\hspace{-0.03cm} X \cdot (1-UX)}{1- U X}= \frac{X}{1- U X}\hspace{0.05cm}.$$
- The entire graph $\rm (D)$ can then be replaced by a single connection from $S_0$ to $S_0\hspace{0.01cm}'$. According to the feedback rule, one obtains for the "enhanced path weighting enumerator function":
- \[T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} \hspace{0.05cm}.\]
- With the series expansion $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $ can also be written for this purpose:
- \[T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \big [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.\]
- Setting the formal input variable $U = 1$, we obtain the "simple path weighting enumerator function", which alone allows statements about the weighting distribution of the output sequence $\underline{x}$:
- \[T(X) = X^5 \cdot \big [ 1 + 2 X + 4 X^2 + 8 X^3 +\text{...}\hspace{0.05cm} \big ] \hspace{0.05cm}.\]
We have already read the same result from the trellis diagram in section "Path weighting enumerator function" . There was
- one gray path with weight $5$,
- two yellow paths with weighting $6$
- four green paths with weighting $7$
- and ... .
Block error probability vs. burst error probability
The simple model according to the sketch is valid for linear block codes as well as for convolutional codes.
»Block codes«
For block codes denote $\underline{u} = (u_1, \ \text{...} \hspace{0.05cm}, \ u_i, \ \text{...} \hspace{0.05cm}, \ u_k)$ and $\underline{v} = (v_1, \ \text{...} \hspace{0.05cm}, v_i, \ \text{...} \hspace{0.05cm} \ , \ v_k)$ the information blocks at the input and output of the system.
Thus, the following descriptive variables can be specified:
- the »block error probability« ${\rm Pr(block\:error)} = {\rm Pr}(\underline{v} ≠ \underline{u}),$
- the »bit error probability« ${\rm Pr(bit\:error)} = {\rm Pr}(v_i ≠ u_i).$
$\text{Please note:}$ In real transmission systems, due to thermal noise the following always applies:
- $${\rm Pr(bit\:error)} > 0\hspace{0.05cm},\hspace{0.5cm}{\rm Pr(block\:error)} > {\rm Pr(bit\:error)} \hspace{0.05cm}.$$
For this a simple explanation attempt: If the decoder decides in each block of length $k$ exactly one bit wrong,
- so the average bit error probability ${\rm Pr(bit\:error)}= 1/k$,
- while for the block error probability ${\rm Pr(block\:error)}\equiv 1$ holds.
»Convolutional codes«
For convolutional codes, the block error probability cannot be specified, since here $\underline{u} = (u_1, \ u_2, \ \text{...} \hspace{0.05cm})$ and $\underline{\upsilon} = (v_1, \ v_2, \ \text{...} \hspace{0.05cm})$ represent sequences.
Even the smallest possible code parameter $k = 1$, leads here to the sequence length $k \hspace{0.05cm}' → ∞$, and
- the block error probability would always result in ${\rm Pr(block\hspace{0.1cm} error)}\equiv 1$,
- even if the bit error probability is extremely small $\hspace{0.05cm}$ $($but non-zero$)$.
$\text{Definition:}$ For the »burst error probability « of a convolutional code holds:
- \[{\rm Pr(burst\:error)} = {\rm Pr}\big \{ {\rm Decoder\hspace{0.15cm} leaves\hspace{0.15cm} the\hspace{0.15cm} correct\hspace{0.15cm}path}\hspace{0.15cm}{\rm at\hspace{0.15cm}time \hspace{0.10cm}\it t}\big \} \hspace{0.05cm}.\]
- To simplify the notation for the following derivation, we always assume the zero sequence $\underline{0}$ which is shown in red in the drawn trellis as the "zero path" $\varphi_0$.
- All other paths $\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} $ $($and many more$)$ leave $\varphi_0$ at time $t$.
- They all belong to the path set ${\it \Phi}$ which is defined as "Viterbi decoder leaves the correct path at time $t$". This probability is calculated in the next section.
Burst error probability and Bhattacharyya bound
We proceed as in the earlier chapter "Bounds for block error probability"
- from the pairwise error probability ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$
- that instead of the path $\varphi_0$
- the decoder could select the path $\varphi_i$.
All considered paths $\varphi_i$ leave the zero path $\varphi_0$ at time $t$; thus they all belong to the path set ${\it \Phi}$.
The sought "burst error probability" is equal to the following union set:
- $${\rm Pr(burst\:error)}= {\rm Pr}\left (\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}\big] \hspace{0.05cm}\cup\hspace{0.05cm}\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}\big]\hspace{0.05cm}\cup\hspace{0.05cm} \text{... }\hspace{0.05cm} \right )$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr(burst\:error)}= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} \big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big] \right )\hspace{0.05cm}.$$
- An upper bound for this is provided by the so-called $\text{Union Bound}$:
- \[{\rm Pr(Burst\:error)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} {\rm Pr}\big [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big ] = {\rm Pr(union \hspace{0.15cm}bound)} \hspace{0.05cm}.\]
- The pairwise error probability can be estimated using the $\text{Bhattacharyya bound}$:
- \[{\rm Pr}\big [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\big ] \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] \le \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.\]
- Here denotes
- $w_{\rm H}(\underline{x}_i)$ is the Hamming weight of the possible encoded sequence $\underline{x}_i,$
- $\ w(\varphi_i)$ is the path weight of the corresponding path $\varphi_i ∈ {\it \Phi},$
- $\beta$ is the so-called $\text{Bhattacharyya parameter}$.
- $\beta$ is the so-called $\text{Bhattacharyya parameter}$.
By »summing over all paths« and comparing with the (simple) $\text{path weighting function}$ $T(X)$ we get the result:
- \[{\rm Pr(burst\:error)} \le T(X = \beta),\hspace{0.5cm}{\rm with}\hspace{0.5cm} T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi} }\hspace{0.15cm} \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.\]
$\text{Example 4: }$ For our standard encoder with
- code rate $R = 1/2$,
- memory $m = 2$,
- D– transfer function $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D)$,
we have obtained the following $\text{path weighting enumerator function}$:
- \[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + \ \text{...} \hspace{0.1cm} = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ \ \text{...} \hspace{0.1cm}) \hspace{0.05cm}.\]
- Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \hspace{0.15cm} $ can also be written for this purpose:
- \[T(X) = \frac{X^5}{1-2 \cdot X} \hspace{0.05cm}.\]
- The BSC model provides the following Bhattacharyya bound with the falsification probability $\varepsilon$:
- \[{\rm Pr(Burst\:error)} \le T(X = \beta) = T\big ( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)} \big ) = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.\]
- In the "Exercise 3.14" this equation is to be evaluated numerically.
Bit error probability and Viterbi bound
Finally, an upper bound is given for the bit error probability. According to the graph, we proceed as in [Liv10][1] assume the following conditions:
- The zero sequence $\underline{x} = \underline{0}$ was sent ⇒ Path $\varphi_0$.
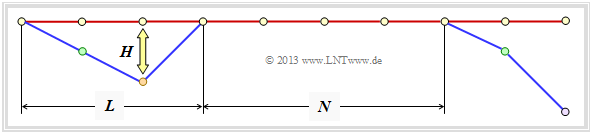
- The duration of a path deviation $($"error burst duration"$)$ is denoted by $L$ .
- The distance between two bursts $($"inter burst time"$)$ we call $N$.
- The Hamming weight of the error bundle be $H$.
For a rate $1/n$ convolutional code ⇒ $k = 1$ ⇒ one information bit per clock, the expected values ${\rm E}\big[L \big]$, ${\rm E}\big[N \big]$ and ${\rm E}\big[H\big]$ of the random variables defined above to give an upper bound for the bit error probability:
- \[{\rm Pr(bit\:error)} = \frac{{\rm E}\big[H\big]}{{\rm E}[L] + {\rm E}\big[N\big]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}\big[H\big]}{{\rm E}\big[N\big]} \hspace{0.05cm}.\]
It is assumed that
- the (mean) duration of an error burst is in practice much smaller than the expected distance between two bursts,
- the (mean) inter burst time $E\big[N\big]$ is equal to the inverse of the burst error probability,
- the expected value in the numerator is estimated as follows:
- \[{\rm E}\big[H \big] \le \frac{1}{\rm Pr(burst\:error)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
In deriving this bound, the "pairwise error probability" ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ and the "Bhattacharyya estimation" are used. Thus we obtain with
- the path input weighting $u(\varphi_i),$
- the path output weighting $w(\varphi_i),$ and
- the Bhattacharyya parameter $\beta$
the following estimation for the bit error probability and refer to it as the »Viterbi bound«:
- \[{\rm Pr(bit\:error)}\le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
This intermediate result can also be represented in another form. We recall the $\text{enhanced path weighting enumerator function}$
- \[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.05cm}.\]
If we derive this function according to the dummy input variable $U$, we get
- \[\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} \hspace{0.05cm}.\]
Finally, if we set $U = 1$ for the dummy input variable, than we see the connection to the above result:
- \[\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.\]
$\text{Conclusion:}$ The »bit error probability« of a convolutional code can be estimated using the extended path weighting enumerator function in closed form:
- \[{\rm Pr(bit\:error)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{ {\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1} } \hspace{0.05cm}.\]
- One speaks of the »Viterbi bound». Here one derives the enhanced path weighting enumerator function after the second parameter $U$ and then sets
- $$X = \beta,\hspace{0.4cm} U = 1.$$
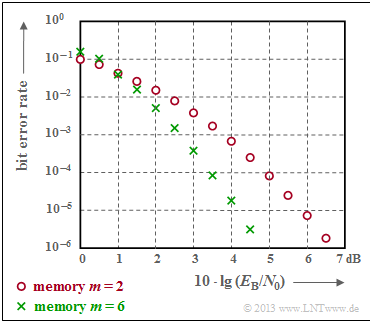
$\text{Example 5:}$ The graph illustrates the good correction capability ⇒ small bit error rate $\rm (BER)$ of convolutional codes at the $\text{$\rm AWGN$ channel}$.
- Red circles denote the $\rm BER$ for our "rate $1/2$ standard encoder" with memory $m = 2$.
- Green crosses mark a convolutional code with $m = 6$, the so-called $\text{industry standard code}$.
- Codes with large memory $m$ lead to large gains over uncoded transmission.
Note:
In "Exercise 3.14", the "Viterbi bound" and the "Bhattacharyya bound" are evaluated numerically for the "rate $1/2$ standard encoder" and the $\text{BSC model}$.
Exercises for the chapter
Exercise 3.12: Path Weighting Function
Exercise 3.12Z: Ring and Feedback
Exercise 3.13: Path Weighting Function again
Exercise 3.14: Error Probability Bounds
References
- ↑ Liva, G.: Channel Coding. Lecture manuscript, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.