Difference between revisions of "Channel Coding/Basics of Convolutional Coding"
| (52 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Convolutional Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Error Probability and Areas of Application |
| − | |Nächste Seite= | + | |Nächste Seite=Algebraic and Polynomial Description |
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE THIRD MAIN CHAPTER # == |
| + | <br> | ||
| + | This third main chapter discusses »'''convolutional codes'''«, first described in 1955 by [https://en.wikipedia.org/wiki/Peter_Elias $\text{Peter Elias}$] [Eli55]<ref name='Eli55'>Elias, P.: Coding for Noisy Channels. In: IRE Conv. Rec. Part 4, pp. 37-47, 1955.</ref>. | ||
| − | + | *While for linear block codes $($see [[Channel_Coding/Objective_of_Channel_Coding#.23_OVERVIEW_OF_THE_FIRST_MAIN_CHAPTER_.23|$\text{first main chapter}$]]$)$ and Reed-Solomon codes $($see [[Channel_Coding/Some_Basics_of_Algebra#.23_OVERVIEW_OF_THE_SECOND_MAIN_CHAPTER_.23|$\text{second main chapter}$]]$)$ the code word length is $n$ in each case, | |
| − | + | *the theory of convolutional codes is based on "semi-infinite" information and encoded sequences. Similarly, "maximum likelihood decoding" using the [[Channel_Coding/Decoding_of_Convolutional_Codes#Viterbi_algorithm_based_on_correlation_and_metrics|$\text{Viterbi algorithm}$]] per se yields the entire sequence. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Specifically, this chapter discusses: | ||
| − | == | + | #Important definitions for convolutional codes: »code rate«, »memory«, » influence length«, » free distance«, |
| + | #»similarities« and »differences« to linear block codes, | ||
| + | #»generator matrix« and »transfer function matrix« of a convolutional code, | ||
| + | #»fractional-rational transfer functions« for systematic convolutional codes, | ||
| + | #description with »state transition diagram« and »trellis diagram«, | ||
| + | #»termination« and »puncturing« of convolutional codes, | ||
| + | #»decoding« of convolutional codes ⇒ »Viterbi algorithm«, | ||
| + | #»weight enumerator functions« and approximations for the »bit error probability«. | ||
| + | |||
| + | |||
| + | |||
| + | == Requirements and definitions == | ||
<br> | <br> | ||
| − | + | We consider in this chapter an infinite binary information sequence $\underline{u}$ and divide it into information blocks $\underline{u}_i$ of $k$ bits each. One can formalize this fact as follows: | |
| − | ::<math>\underline{\it u} = \left ( \underline{\it u}_1, \underline{\it u}_2, ... \hspace{0. | + | ::<math>\underline{\it u} = \left ( \underline{\it u}_1, \underline{\it u}_2, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \underline{\it u}_i , \hspace{0.05cm} \text{...} \hspace{0.05cm}\right ) \hspace{0.3cm}{\rm with}\hspace{0.3cm} \underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, u_i^{(k)}\right )\hspace{0.05cm},</math> |
| − | ::<math>u_i^{(j)}\in {\rm GF(2)}\hspace{0.3cm}{\rm | + | ::<math>u_i^{(j)}\in {\rm GF(2)}\hspace{0.3cm}{\rm for} \hspace{0.3cm}1 \le j \le k |
\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \underline{\it u}_i \in {\rm GF}(2^k)\hspace{0.05cm}.</math> | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \underline{\it u}_i \in {\rm GF}(2^k)\hspace{0.05cm}.</math> | ||
| − | + | Such a sequence without negative indices is called »'''semi–infinite'''«.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ In a »<b>binary convolutional code</b>«, a code word $\underline{x}_i$ consisting of $n$ code bit is output at time $i$: |
| + | |||
| + | ::<math>\underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, x_i^{(n)}\right )\in {\rm GF}(2^n)\hspace{0.05cm}.</math> | ||
| + | |||
| + | This results according to | ||
| + | *the $k$ bit of the current information block $\underline{u}_i$, and <br> | ||
| − | + | *the $m$ previous information blocks $\underline{u}_{i-1}$, ... , $\underline{u}_{i-m}$.<br>}}<br> | |
| − | + | [[File:EN_KC_T_3_1_S1_neu.png|right|frame|Dependencies for a convolutional encoder with $m = 2$|class=fit]] | |
| − | |||
| − | + | The diagram opposite illustrates this fact for the parameters | |
| + | :$$k = 4, \ n = 7, \ m = 2,\ i = 4.$$ | ||
| − | + | The $n = 7$ code bits $x_4^{(1)}$, ... , $x_4^{(7)}$ generated at time $i = 4$ may depend $($directly$)$ on the $k \cdot (m+1) = 12$ information bits marked in red and are generated by modulo-2 additions.<br> | |
| − | + | Drawn in yellow is a $(n, k)$ convolutional encoder. Note that the vector $\underline{u}_i$ and the sequence $\underline{u}^{(i)}$ are fundamentally different: | |
| + | *While $\underline{u}_i = (u_i^{(1)}, u_i^{(2)}$, ... , $u_i^{(k)})$ summarizes $k$ parallel information bits at time $i$, | ||
| − | + | * $\underline{u}^i = (u_1^{(i)}$, $u_2^{(i)}, \ \text{...})$ denotes the $($horizontal$)$ sequence at $i$–th input of the convolutional encoder. | |
| − | * | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Some definitions related to convolutional codes:}$ |
| − | * | + | *The »<b>code rate</b>« results as for the block codes to $R = k/n$.<br> |
| − | * | + | *Perceive $m$ as the »<b>memory</b>« of the code and the "convolutional code" itself with ${\rm CC} \ (n, k, m)$.<br> |
| − | * | + | *This gives the »<b>constraint length</b>« $\nu = m + 1$ of the convolutional code.<br> |
| − | * | + | *For $k > 1$ one often gives these parameters also in bits: $m_{\rm bit} = m \cdot k$ resp. $\nu_{\rm bit} = (m + 1) \cdot k$.<br>}} |
| − | == | + | == Similarities and differences compared to block codes == |
<br> | <br> | ||
| − | + | From the [[Channel_Coding/Basics_of_Convolutional_Coding#Requirements_and_definitions| $\text{definition}$]] in the previous section, it is evident that a binary convolutional code with $m = 0$ $($i.e., without memory$)$ would be identical to a binary block code as described in the first main chapter. We exclude this limiting case and therefore assume always for the following: | |
| − | * | + | *The memory $m$ be greater than or equal to $1$.<br> |
| − | * | + | *The influence length $\nu$ be greater than or equal to $2$.<br><br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ For a $(7, 4)$ block code, the code word $\underline {x}_4$ depends only on the information word $\underline{u}_4$ but not on $\underline{u}_2$ and $\underline{u}_3$, as in the [[Channel_Coding/Basics_of_Convolutional_Coding#Requirements_and_definitions| $\text{example convolutional codes}$]] $($with $m = 2)$ in the last section.<br> |
| − | [[File: | + | [[File:EN_KC_T_3_1_S2.png|right|frame|Dependencies on a $(7, 4)$ block code at time $i = 4$|class=fit]] |
| − | |||
| − | |||
| − | |||
| + | For example, if | ||
| + | :$$x_4^{(1)} = u_4^{(1)}, \ x_4^{(2)} = u_4^{(2)},$$ | ||
| + | :$$x_4^{(3)} = u_4^{(3)}, \ x_4^{(4)} = u_4^{(4)}$$ | ||
| + | as well as | ||
:$$x_4^{(5)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(3)}\hspace{0.05cm},$$ | :$$x_4^{(5)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(3)}\hspace{0.05cm},$$ | ||
:$$x_4^{(6)} = u_4^{(2)}+ u_4^{(3)}+u_4^{(4)}\hspace{0.05cm},$$ | :$$x_4^{(6)} = u_4^{(2)}+ u_4^{(3)}+u_4^{(4)}\hspace{0.05cm},$$ | ||
:$$x_4^{(7)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(4)}\hspace{0.05cm},$$ | :$$x_4^{(7)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(4)}\hspace{0.05cm},$$ | ||
| − | so | + | applies then it is a so-called [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes| $\text{systematic Hamming code}$]] $\text{HS (7, 4, 3)}$. In the graph, these special dependencies for $x_4^{(1)}$ and $x_4^{(7)}$ are drawn in red.}}<br> |
| − | In | + | In a sense, one could also interpret a $(n, k)$ convolutional code with memory $m ≥ 1$ as a block code whose code parameters $n\hspace{0.05cm}' \gg n$ and $k\hspace{0.05cm}' \gg k$ would have to assume much larger values than those of the present convolutional code. |
| − | |||
| − | + | However, because of the large differences in description, properties, and especially decoding, we consider convolutional codes to be something completely new in this learning tutorial. The reasons for this are as follows: | |
| + | # A block encoder converts block-by-block information words of length $k$ bits into code words of length $n$ bits each. In this case, the larger its code word length $n$, the more powerful the block code is. For a given code rate $R = k/n$ this also requires a large information word length $k$.<br> | ||
| + | # In contrast, the correction capability of a convolutional code is essentially determined by its memory $m$. The code parameters $k$ and $n$ are mostly chosen very small here $(1, \ 2, \ 3, \ \text{...})$. Thus, only very few and, moreover, very simple convolutional codes are of practical importance.<br> | ||
| + | # Even with small values for $k$ and $n$, a convolutional encoder transfers a whole sequence of information bits $(k\hspace{0.05cm}' → ∞)$ into a very long sequence of code bits $(n\hspace{0.05cm}' = k\hspace{0.05cm}'/R)$. Such a code thus often provides a large correction capability as well.<br> | ||
| + | # There are efficient convolutional decoders, for example the [[Channel_Coding/Decoding_of_Convolutional_Codes#Viterbi_algorithm_based_on_correlation_and_metrics|$\text{Viterbi algorithm}$]] and the [[Channel_Coding/Soft-in_Soft-Out_Decoder#BCJR_decoding:_Forward-backward_algorithm| $\text{BCJR algorithm}$]], which can process reliability information about the channel ⇒ "soft decision input" and provide reliability information about the decoding result ⇒ "soft decision output".<br> | ||
| + | # Please note: The terms "convolutional code" and "convolutional encoder" should not be confused: | ||
| + | ::*The "convolutional code" ${\rm CC} \ (n, \ k, \ m)$ ⇒ $R = k/n$ is understood as "the set of all possible encoded sequences $\underline{x}$ $($at the output$)$ that can be generated with this code considering all possible information sequences $\underline{u}$ $($at the input$)$". | ||
| + | |||
| + | ::*There are several "convolutional encoders" that realize the same "convolutional code".<br> | ||
| − | + | == Rate 1/2 convolutional encoder == | |
| + | <br> | ||
| + | [[File:EN_KC_T_3_1_S3ab.png|right|frame|Convolutional encoder $(n = 2, \hspace{0.05cm} k = 1)$ for one bit $u_i$ $($upper graphic$)$ and for the information sequence $\underline{u}$ $($lower graphic$)$|class=fit]] | ||
| − | + | The upper graph shows a $(n = 2, \hspace{0.05cm} k = 1)$ convolutional encoder. | |
| − | = | + | *At clock time $i$ the information bit $u_i$ is present at the encoder input and the $2$–bit code block $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ is output. |
| − | + | ||
| − | + | *To generate two code bits $x_i^{(1)}$ and $x_i^{(2)}$ from a single information bit, the convolutional encoder must include at least one memory element: | |
| − | + | :$$k = 1\hspace{0.05cm}, \ n = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} m \ge 1 | |
| + | \hspace{0.05cm}.$$ | ||
| − | + | *Taking into account the $($half–infinite$)$ long information sequence $\underline{u}$ the model results according to the lower graph. | |
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ The graphic shows a convolutional encoder for the parameters $k = 1, \ n = 2$ and $m = 1$. | ||
| − | [[File: | + | [[File:EN_KC_T_3_1_S3c.png|right|frame|Convolutional encoder with $k = 1, \ n = 2, \ m = 1$ and example sequences; the square with label $D$ $($"delay"$)$ indicates a memory element. |class=fit]] |
| − | |||
| − | * | + | *This is a "systematic" convolutional encoder, characterized by |
| − | + | :$$x_i^{(1)} = u_i.$$ | |
| − | + | *The second output returns $x_i^{(2)} = u_i + u_{i-1}$. | |
| − | |||
| − | { | + | *In the example output sequence $\underline{x}$ after multiplexing |
| − | $ | + | :*all $x_i^{(1)}$ are labeled red, |
| − | + | :*all $x_i^{(2)}$ are labeled blue.}}<br> | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 3:}$ | ||
| + | The graphic shows a $(n = 2, \ k = 1)$ convolutional encoder with $m = 2$ memory elements: | ||
| + | |||
| + | *On the left is shown the equivalent circuit. | ||
| − | + | *On the right you see a realization form of this encoder. | |
| − | + | *The two information bits are: | |
| − | + | [[File:EN_KC_T_3_1_S3d_neu.png|right|frame|Convolutional encoder $(k = 1, \ n = 2, \ m = 2)$ in two different representations|class=fit]] | |
| − | |||
| − | [[File: | ||
| − | + | ::<math>x_i^{(1)} = u_{i} + u_{i-1}+ u_{i-2} \hspace{0.05cm},</math> | |
| + | ::<math>x_i^{(2)} = u_{i} + u_{i-2} \hspace{0.05cm}.</math> | ||
| − | + | *Because $x_i^{(1)} ≠ u_i$ this is not a systematic code. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | It can be seen: | |
| + | # The input sequence $\underline{u}$ is stored in a shift register of length $L = m + 1 = 3$ .<br> | ||
| + | #At clock time $i$ the left memory element contains the current information bit $u_i$, which is shifted one place to the right at each of the next clock times.<br> | ||
| + | #The number of yellow squares gives the memory $m = 2$ of the encoder.<br><br> | ||
| − | + | ⇒ From these plots it is clear that $x_i^{(1)}$ and $x_i^{(2)}$ can each be interpreted as the output of a [[Theory_of_Stochastic_Signals/Digital_Filters|$\text{digital filter}$]] over the Galois field ${\rm GF(2)}$ where both filters operate in parallel with the same input sequence $\underline{u}$ . | |
| − | + | ⇒ Since $($in general terms$)$, the output signal of a filter results from the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_time_domain|$\text{convolution}$]] of the input signal with the filter impulse response, this is referred to as "convolutional coding".<br>}} | |
| − | + | == Convolutional encoder with two inputs == | |
| + | <br> | ||
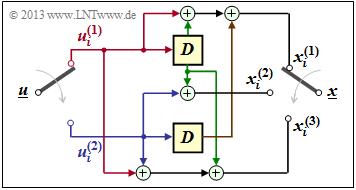
| + | [[File:P ID2598 KC T 3 1 S4 v1.png|right|frame|Convolutional encoder with $k = 2$ and $n = 3$]] | ||
| + | Now consider a convolutional encoder that generates $n = 3$ code bits from $k = 2$ information bits. | ||
| + | *The information sequence $\underline{u}$ is divided into blocks of two bits each. | ||
| + | |||
| + | *At the clock time $i$: The bit $u_i^{(1)}$ is present at the upper input and $u_i^{(2)}$ at the lower input. | ||
| − | + | *Then holds for the $n = 3$ code bits at time $i$: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
::<math>x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},</math> | ::<math>x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},</math> | ||
::<math>x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},</math> | ::<math>x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},</math> | ||
::<math>x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.</math> | ::<math>x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.</math> | ||
| − | In | + | In the graph, the info–bits $u_i^{(1)}$ and $u_i^{(2)}$ are marked red resp. blue, and the previous info–bits $u_{i-1}^{(1)}$ resp. $u_{i-1}^{(2)}$ are marked green and brown, respectively |
| − | + | To be noted: | |
| − | + | # The "memory" $m$ is equal to the maximum memory cell count in a branch ⇒ here $m = 1$. | |
| + | # The "influence length" $\nu$ is equal to the sum of all memory elements ⇒ here $\nu = 2$.<br> | ||
| + | # All memory elements are set to zero at the beginning of the coding $($"initialization"$)$. | ||
| + | # The code defined herewith is the set of all possible encoded sequences $\underline{x}$, which result when all possible information sequences $\underline{u}$ are entered. | ||
| + | # Both $\underline{u}$ and $\underline{x}$ are thereby (temporally) unbounded.<br> | ||
| − | |||
| − | * | + | {{GraueBox|TEXT= |
| + | $\text{Example 4:}$ Let the information sequence be $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1, \ \text{ ...})$. This gives the subsequences | ||
| + | *$\underline{u}^{(1)} = (0, 1, 0, 1, \ \text{ ...})$, | ||
| + | *$\underline{u}^{(2)} = (1, 0, 0, 1, \ \text{ ...})$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | With the specification $u_0^{(1)} = u_0^{(2)} = 0$ it follows from the above equations for the $n = 3$ code bits. | |
| − | * | + | *at the first coding step $(i = 1)$: |
::<math>x_1^{(1)} = u_{1}^{(1)} = 0 \hspace{0.05cm},\hspace{0.4cm} | ::<math>x_1^{(1)} = u_{1}^{(1)} = 0 \hspace{0.05cm},\hspace{0.4cm} | ||
| Line 173: | Line 197: | ||
x_1^{(3)} = u_{1}^{(1)} + u_{1}^{(2)} = 0+1 = 1 \hspace{0.05cm},</math> | x_1^{(3)} = u_{1}^{(1)} + u_{1}^{(2)} = 0+1 = 1 \hspace{0.05cm},</math> | ||
| − | * | + | *at the second coding step $(i = 2)$: |
::<math>x_2^{(1)} =u_{2}^{(1)} + u_{1}^{(1)}+ u_{1}^{(2)} = 1 + 0 + 1 = 0\hspace{0.05cm},\hspace{0.4cm} | ::<math>x_2^{(1)} =u_{2}^{(1)} + u_{1}^{(1)}+ u_{1}^{(2)} = 1 + 0 + 1 = 0\hspace{0.05cm},\hspace{0.4cm} | ||
| Line 179: | Line 203: | ||
x_2^{(3)} = u_{2}^{(1)} + u_{2}^{(2)}+ u_{1}^{(1)} = 1 + 0+0 =1\hspace{0.05cm},</math> | x_2^{(3)} = u_{2}^{(1)} + u_{2}^{(2)}+ u_{1}^{(1)} = 1 + 0+0 =1\hspace{0.05cm},</math> | ||
| − | * | + | *at the third coding step $(i = 3)$: |
::<math>x_3^{(1)} =u_{3}^{(1)} + u_{2}^{(1)}+ u_{2}^{(2)} = 0+1+0 = 1\hspace{0.05cm},\hspace{0.4cm} | ::<math>x_3^{(1)} =u_{3}^{(1)} + u_{2}^{(1)}+ u_{2}^{(2)} = 0+1+0 = 1\hspace{0.05cm},\hspace{0.4cm} | ||
| Line 185: | Line 209: | ||
x_3^{(3)} =u_{3}^{(1)} + u_{3}^{(2)}+ u_{2}^{(1)} = 0+0+1 =1\hspace{0.05cm},</math> | x_3^{(3)} =u_{3}^{(1)} + u_{3}^{(2)}+ u_{2}^{(1)} = 0+0+1 =1\hspace{0.05cm},</math> | ||
| − | * | + | *and finally at the fourth coding step $(i = 4)$: |
::<math>x_4^{(1)} = u_{4}^{(1)} + u_{3}^{(1)}+ u_{3}^{(2)} = 1+0+0 = 1\hspace{0.05cm},\hspace{0.4cm} | ::<math>x_4^{(1)} = u_{4}^{(1)} + u_{3}^{(1)}+ u_{3}^{(2)} = 1+0+0 = 1\hspace{0.05cm},\hspace{0.4cm} | ||
| Line 191: | Line 215: | ||
x_4^{(3)}= u_{4}^{(1)} + u_{4}^{(2)}+ u_{3}^{(1)} = 1+1+0 =0\hspace{0.05cm}.</math> | x_4^{(3)}= u_{4}^{(1)} + u_{4}^{(2)}+ u_{3}^{(1)} = 1+1+0 =0\hspace{0.05cm}.</math> | ||
| − | + | Thus the encoded sequence is after the multiplexer: $\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, \ \text{...})$.}}<br> | |
| − | == | + | == Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.1:_Analysis_of_a_Convolutional_Encoder|Exercise 3.1: Analysis of a Convolutional Encoder]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.1Z:_Convolution_Codes_of_Rate_1/2|Exercise 3.1Z: Convolution Codes of Rate 1/2]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:02, 7 December 2022
Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
This third main chapter discusses »convolutional codes«, first described in 1955 by $\text{Peter Elias}$ [Eli55][1].
- While for linear block codes $($see $\text{first main chapter}$$)$ and Reed-Solomon codes $($see $\text{second main chapter}$$)$ the code word length is $n$ in each case,
- the theory of convolutional codes is based on "semi-infinite" information and encoded sequences. Similarly, "maximum likelihood decoding" using the $\text{Viterbi algorithm}$ per se yields the entire sequence.
Specifically, this chapter discusses:
- Important definitions for convolutional codes: »code rate«, »memory«, » influence length«, » free distance«,
- »similarities« and »differences« to linear block codes,
- »generator matrix« and »transfer function matrix« of a convolutional code,
- »fractional-rational transfer functions« for systematic convolutional codes,
- description with »state transition diagram« and »trellis diagram«,
- »termination« and »puncturing« of convolutional codes,
- »decoding« of convolutional codes ⇒ »Viterbi algorithm«,
- »weight enumerator functions« and approximations for the »bit error probability«.
Requirements and definitions
We consider in this chapter an infinite binary information sequence $\underline{u}$ and divide it into information blocks $\underline{u}_i$ of $k$ bits each. One can formalize this fact as follows:
- \[\underline{\it u} = \left ( \underline{\it u}_1, \underline{\it u}_2, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \underline{\it u}_i , \hspace{0.05cm} \text{...} \hspace{0.05cm}\right ) \hspace{0.3cm}{\rm with}\hspace{0.3cm} \underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, u_i^{(k)}\right )\hspace{0.05cm},\]
- \[u_i^{(j)}\in {\rm GF(2)}\hspace{0.3cm}{\rm for} \hspace{0.3cm}1 \le j \le k \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \underline{\it u}_i \in {\rm GF}(2^k)\hspace{0.05cm}.\]
Such a sequence without negative indices is called »semi–infinite«.
$\text{Definition:}$ In a »binary convolutional code«, a code word $\underline{x}_i$ consisting of $n$ code bit is output at time $i$:
- \[\underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm} \text{...} \hspace{0.05cm}, x_i^{(n)}\right )\in {\rm GF}(2^n)\hspace{0.05cm}.\]
This results according to
- the $k$ bit of the current information block $\underline{u}_i$, and
- the $m$ previous information blocks $\underline{u}_{i-1}$, ... , $\underline{u}_{i-m}$.
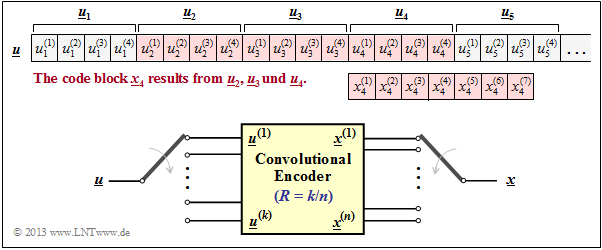
The diagram opposite illustrates this fact for the parameters
- $$k = 4, \ n = 7, \ m = 2,\ i = 4.$$
The $n = 7$ code bits $x_4^{(1)}$, ... , $x_4^{(7)}$ generated at time $i = 4$ may depend $($directly$)$ on the $k \cdot (m+1) = 12$ information bits marked in red and are generated by modulo-2 additions.
Drawn in yellow is a $(n, k)$ convolutional encoder. Note that the vector $\underline{u}_i$ and the sequence $\underline{u}^{(i)}$ are fundamentally different:
- While $\underline{u}_i = (u_i^{(1)}, u_i^{(2)}$, ... , $u_i^{(k)})$ summarizes $k$ parallel information bits at time $i$,
- $\underline{u}^i = (u_1^{(i)}$, $u_2^{(i)}, \ \text{...})$ denotes the $($horizontal$)$ sequence at $i$–th input of the convolutional encoder.
$\text{Some definitions related to convolutional codes:}$
- The »code rate« results as for the block codes to $R = k/n$.
- Perceive $m$ as the »memory« of the code and the "convolutional code" itself with ${\rm CC} \ (n, k, m)$.
- This gives the »constraint length« $\nu = m + 1$ of the convolutional code.
- For $k > 1$ one often gives these parameters also in bits: $m_{\rm bit} = m \cdot k$ resp. $\nu_{\rm bit} = (m + 1) \cdot k$.
Similarities and differences compared to block codes
From the $\text{definition}$ in the previous section, it is evident that a binary convolutional code with $m = 0$ $($i.e., without memory$)$ would be identical to a binary block code as described in the first main chapter. We exclude this limiting case and therefore assume always for the following:
- The memory $m$ be greater than or equal to $1$.
- The influence length $\nu$ be greater than or equal to $2$.
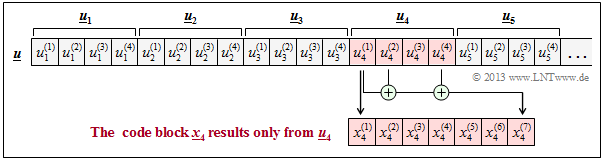
$\text{Example 1:}$ For a $(7, 4)$ block code, the code word $\underline {x}_4$ depends only on the information word $\underline{u}_4$ but not on $\underline{u}_2$ and $\underline{u}_3$, as in the $\text{example convolutional codes}$ $($with $m = 2)$ in the last section.
For example, if
- $$x_4^{(1)} = u_4^{(1)}, \ x_4^{(2)} = u_4^{(2)},$$
- $$x_4^{(3)} = u_4^{(3)}, \ x_4^{(4)} = u_4^{(4)}$$
as well as
- $$x_4^{(5)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(3)}\hspace{0.05cm},$$
- $$x_4^{(6)} = u_4^{(2)}+ u_4^{(3)}+u_4^{(4)}\hspace{0.05cm},$$
- $$x_4^{(7)} = u_4^{(1)}+ u_4^{(2)}+u_4^{(4)}\hspace{0.05cm},$$
applies then it is a so-called $\text{systematic Hamming code}$ $\text{HS (7, 4, 3)}$. In the graph, these special dependencies for $x_4^{(1)}$ and $x_4^{(7)}$ are drawn in red.
In a sense, one could also interpret a $(n, k)$ convolutional code with memory $m ≥ 1$ as a block code whose code parameters $n\hspace{0.05cm}' \gg n$ and $k\hspace{0.05cm}' \gg k$ would have to assume much larger values than those of the present convolutional code.
However, because of the large differences in description, properties, and especially decoding, we consider convolutional codes to be something completely new in this learning tutorial. The reasons for this are as follows:
- A block encoder converts block-by-block information words of length $k$ bits into code words of length $n$ bits each. In this case, the larger its code word length $n$, the more powerful the block code is. For a given code rate $R = k/n$ this also requires a large information word length $k$.
- In contrast, the correction capability of a convolutional code is essentially determined by its memory $m$. The code parameters $k$ and $n$ are mostly chosen very small here $(1, \ 2, \ 3, \ \text{...})$. Thus, only very few and, moreover, very simple convolutional codes are of practical importance.
- Even with small values for $k$ and $n$, a convolutional encoder transfers a whole sequence of information bits $(k\hspace{0.05cm}' → ∞)$ into a very long sequence of code bits $(n\hspace{0.05cm}' = k\hspace{0.05cm}'/R)$. Such a code thus often provides a large correction capability as well.
- There are efficient convolutional decoders, for example the $\text{Viterbi algorithm}$ and the $\text{BCJR algorithm}$, which can process reliability information about the channel ⇒ "soft decision input" and provide reliability information about the decoding result ⇒ "soft decision output".
- Please note: The terms "convolutional code" and "convolutional encoder" should not be confused:
- The "convolutional code" ${\rm CC} \ (n, \ k, \ m)$ ⇒ $R = k/n$ is understood as "the set of all possible encoded sequences $\underline{x}$ $($at the output$)$ that can be generated with this code considering all possible information sequences $\underline{u}$ $($at the input$)$".
- There are several "convolutional encoders" that realize the same "convolutional code".
- There are several "convolutional encoders" that realize the same "convolutional code".
Rate 1/2 convolutional encoder
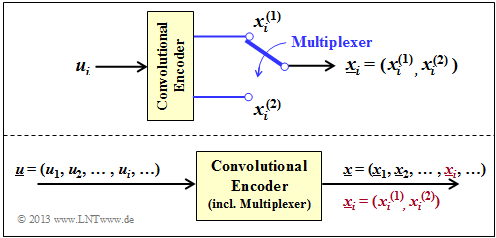
The upper graph shows a $(n = 2, \hspace{0.05cm} k = 1)$ convolutional encoder.
- At clock time $i$ the information bit $u_i$ is present at the encoder input and the $2$–bit code block $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ is output.
- To generate two code bits $x_i^{(1)}$ and $x_i^{(2)}$ from a single information bit, the convolutional encoder must include at least one memory element:
- $$k = 1\hspace{0.05cm}, \ n = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} m \ge 1 \hspace{0.05cm}.$$
- Taking into account the $($half–infinite$)$ long information sequence $\underline{u}$ the model results according to the lower graph.
$\text{Example 2:}$ The graphic shows a convolutional encoder for the parameters $k = 1, \ n = 2$ and $m = 1$.
- This is a "systematic" convolutional encoder, characterized by
- $$x_i^{(1)} = u_i.$$
- The second output returns $x_i^{(2)} = u_i + u_{i-1}$.
- In the example output sequence $\underline{x}$ after multiplexing
- all $x_i^{(1)}$ are labeled red,
- all $x_i^{(2)}$ are labeled blue.
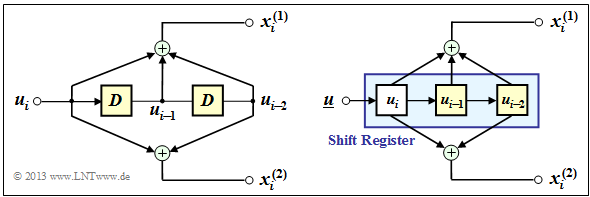
$\text{Example 3:}$ The graphic shows a $(n = 2, \ k = 1)$ convolutional encoder with $m = 2$ memory elements:
- On the left is shown the equivalent circuit.
- On the right you see a realization form of this encoder.
- The two information bits are:
- \[x_i^{(1)} = u_{i} + u_{i-1}+ u_{i-2} \hspace{0.05cm},\]
- \[x_i^{(2)} = u_{i} + u_{i-2} \hspace{0.05cm}.\]
- Because $x_i^{(1)} ≠ u_i$ this is not a systematic code.
It can be seen:
- The input sequence $\underline{u}$ is stored in a shift register of length $L = m + 1 = 3$ .
- At clock time $i$ the left memory element contains the current information bit $u_i$, which is shifted one place to the right at each of the next clock times.
- The number of yellow squares gives the memory $m = 2$ of the encoder.
⇒ From these plots it is clear that $x_i^{(1)}$ and $x_i^{(2)}$ can each be interpreted as the output of a $\text{digital filter}$ over the Galois field ${\rm GF(2)}$ where both filters operate in parallel with the same input sequence $\underline{u}$ .
⇒ Since $($in general terms$)$, the output signal of a filter results from the $\text{convolution}$ of the input signal with the filter impulse response, this is referred to as "convolutional coding".
Convolutional encoder with two inputs
Now consider a convolutional encoder that generates $n = 3$ code bits from $k = 2$ information bits.
- The information sequence $\underline{u}$ is divided into blocks of two bits each.
- At the clock time $i$: The bit $u_i^{(1)}$ is present at the upper input and $u_i^{(2)}$ at the lower input.
- Then holds for the $n = 3$ code bits at time $i$:
- \[x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\]
- \[x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\]
- \[x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]
In the graph, the info–bits $u_i^{(1)}$ and $u_i^{(2)}$ are marked red resp. blue, and the previous info–bits $u_{i-1}^{(1)}$ resp. $u_{i-1}^{(2)}$ are marked green and brown, respectively
To be noted:
- The "memory" $m$ is equal to the maximum memory cell count in a branch ⇒ here $m = 1$.
- The "influence length" $\nu$ is equal to the sum of all memory elements ⇒ here $\nu = 2$.
- All memory elements are set to zero at the beginning of the coding $($"initialization"$)$.
- The code defined herewith is the set of all possible encoded sequences $\underline{x}$, which result when all possible information sequences $\underline{u}$ are entered.
- Both $\underline{u}$ and $\underline{x}$ are thereby (temporally) unbounded.
$\text{Example 4:}$ Let the information sequence be $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1, \ \text{ ...})$. This gives the subsequences
- $\underline{u}^{(1)} = (0, 1, 0, 1, \ \text{ ...})$,
- $\underline{u}^{(2)} = (1, 0, 0, 1, \ \text{ ...})$.
With the specification $u_0^{(1)} = u_0^{(2)} = 0$ it follows from the above equations for the $n = 3$ code bits.
- at the first coding step $(i = 1)$:
- \[x_1^{(1)} = u_{1}^{(1)} = 0 \hspace{0.05cm},\hspace{0.4cm} x_1^{(2)} = u_{1}^{(2)} = 1 \hspace{0.05cm},\hspace{0.4cm} x_1^{(3)} = u_{1}^{(1)} + u_{1}^{(2)} = 0+1 = 1 \hspace{0.05cm},\]
- at the second coding step $(i = 2)$:
- \[x_2^{(1)} =u_{2}^{(1)} + u_{1}^{(1)}+ u_{1}^{(2)} = 1 + 0 + 1 = 0\hspace{0.05cm},\hspace{0.4cm} x_2^{(2)} = u_{2}^{(2)} + u_{1}^{(1)} = 0+0 = 0\hspace{0.05cm},\hspace{0.4cm} x_2^{(3)} = u_{2}^{(1)} + u_{2}^{(2)}+ u_{1}^{(1)} = 1 + 0+0 =1\hspace{0.05cm},\]
- at the third coding step $(i = 3)$:
- \[x_3^{(1)} =u_{3}^{(1)} + u_{2}^{(1)}+ u_{2}^{(2)} = 0+1+0 = 1\hspace{0.05cm},\hspace{0.4cm} x_3^{(2)} = u_{3}^{(2)} + u_{2}^{(1)} = 0+1=1\hspace{0.05cm},\hspace{0.4cm} x_3^{(3)} =u_{3}^{(1)} + u_{3}^{(2)}+ u_{2}^{(1)} = 0+0+1 =1\hspace{0.05cm},\]
- and finally at the fourth coding step $(i = 4)$:
- \[x_4^{(1)} = u_{4}^{(1)} + u_{3}^{(1)}+ u_{3}^{(2)} = 1+0+0 = 1\hspace{0.05cm},\hspace{0.4cm} x_4^{(2)} = u_{4}^{(2)} + u_{3}^{(1)} = 1+0=1\hspace{0.05cm},\hspace{0.4cm} x_4^{(3)}= u_{4}^{(1)} + u_{4}^{(2)}+ u_{3}^{(1)} = 1+1+0 =0\hspace{0.05cm}.\]
Thus the encoded sequence is after the multiplexer: $\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, \ \text{...})$.
Exercises for the chapter
Exercise 3.1: Analysis of a Convolutional Encoder
Exercise 3.1Z: Convolution Codes of Rate 1/2
References
- ↑ Elias, P.: Coding for Noisy Channels. In: IRE Conv. Rec. Part 4, pp. 37-47, 1955.