Difference between revisions of "Aufgaben:Exercise 4.5: On the Extrinsic L-values again"
| (37 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} |
| − | [[File:P_ID3026__KC_A_4_5_v2.png|right|frame| | + | [[File:P_ID3026__KC_A_4_5_v2.png|right|frame|Table for first $L_{\rm E}(i)$ approach]] |
| − | + | We assume as in the [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"theory section"]] the "single parity–check code" $\rm SPC \, (3, \, 2, \, 2)$. | |
| − | + | ||
| + | The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} | ||
\{ \underline{x}_0,\hspace{0.05cm} | \{ \underline{x}_0,\hspace{0.05cm} | ||
\underline{x}_1,\hspace{0.05cm} | \underline{x}_1,\hspace{0.05cm} | ||
\underline{x}_2,\hspace{0.05cm} | \underline{x}_2,\hspace{0.05cm} | ||
| − | \underline{x}_3\} | + | \underline{x}_3\}$ with |
| − | :$$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm | + | :$$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} |
\underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$ | \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$ | ||
| − | :$$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm | + | :$$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} |
\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$ | \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$ | ||
| − | :$$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm | + | :$$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} |
\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$ | \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$ | ||
| − | :$$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm | + | :$$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} |
\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$ | \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$ | ||
| − | In | + | In the exercise we mostly use the second (bipolar) representation of the code symbols: |
| + | :$$x_i ∈ \{+1, -1\}.$$ | ||
| − | + | Note: | |
| + | #It is not that the $\rm SPC \, (3, \, 2, \, 2)$ would be of much practical interest, since, for example, in "hard decision" because of $d_{\rm min} = 2$ only one error can be detected and none can be corrected. | ||
| + | #However, the code is well suited for demonstration purposes because of the manageable effort involved. | ||
| + | #With "iterative symbol-wise decoding" one can also correct one error. | ||
| + | #In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation: | ||
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$ | ||
| − | + | :Here $\underline{x}^{(-1)}$ denotes all symbols except $x_i$ and is thus a vector of length $n - 1 = 2$. | |
| − | |||
| − | |||
| − | + | ⇒ As the »'''first $L_{\rm E}(i)$ approach'''« we refer to the approach corresponding to the equations | |
:$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | ||
:$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | ||
:$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | :$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | ||
| − | + | '''(1)''' This $L_{\rm E}(i)$ approach underlies the results table above $($red entries$)$, assuming the following a-posteriori $L$–values: | |
| − | :$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm} | + | :$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} |
| − | L_1 = +1.0\hspace{0.05cm},\hspace{0. | + | L_1 = +1.0\hspace{0.05cm},\hspace{0.15cm} |
| − | L_2 = +0.4\hspace{0.05cm},\hspace{0. | + | L_2 = +0.4\hspace{0.05cm},\hspace{0.15cm} |
L_3 = -1.0\hspace{0.05cm}.$$ | L_3 = -1.0\hspace{0.05cm}.$$ | ||
| − | + | '''(2)''' The extrinsic $L$–values for the zeroth iteration result in $($derivation in [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|$\text{Exercise 4.5Z})$]]: | |
| + | :$$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$ | ||
| − | + | '''(3)''' The a-posteriori $L$–values at the beginning of the first iteration are thus | |
| − | :$$\underline{ | + | :$$\underline{L_{\rm APP} }^{(I=1)} = \underline{L_{\rm APP} }^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = |
(+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | ||
\hspace{0.05cm} . $$ | \hspace{0.05cm} . $$ | ||
| − | + | '''(4)''' From this, the new extrinsic $L$–values for the iteration loop $I = 1$ are as follows: | |
| − | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \ | + | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$ |
| − | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \ | + | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$ |
| − | + | Further, one can see from the above table: | |
| − | * | + | * A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$ code word. |
| − | |||
| − | |||
| + | * But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$. | ||
| − | + | *Also in later graphs, the rows with correct hard decisions for the first time are highlighted in blue. | |
| − | :$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)]\hspace{0.05cm},$$ | + | |
| + | * Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general. | ||
| + | |||
| + | |||
| + | Besides, in this exercise we consider a »'''second $L_{\rm E}(i)$ approach'''«, which is given here for the example of the first symbol $(i = 1)$: | ||
| + | :$${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},$$ | ||
:$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ | :$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ | ||
| − | + | This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better $($larger$)$ the input log likelihood ratio is completely disregarded. | |
| + | |||
| + | Let us consider two examples for this: | ||
| + | |||
| + | |||
| + | '''(1)''' For $L_2 = 1.0$ and $L_3 = 5.0$ we get | ||
| + | * after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$ | ||
| + | |||
| + | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$ | ||
| + | |||
| + | |||
| + | '''(2)''' On the other hand one obtains for $L_2 = L_3 = 1.0$ | ||
| + | * according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$ | ||
| − | + | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$ | |
| − | * | ||
| − | : | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | One can see the clear discrepancy between the two approaches. The second approach $($approximation$)$ is clearly more positive than the first $($correct$)$ approach. However, it is actually only important that the iterations lead to the desired decoding result. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | <u>Hints:</u> | ||
| + | *The exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. | ||
| + | |||
| + | *Referred to in particular [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"Calculation of extrinsic log likelihood ratios"]]. | ||
| + | |||
| + | * Only the '''second solution approach''' is treated here. | ||
| + | |||
| + | * For the first solution approach we refer to [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|$\text{Exercise 4.5Z}$]] . | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {It holds $\underline{L} = (+1.0, +0.4, -1.0)$. Determine the extrinsic $L$–values according to the '''second $L_{\rm E}(i)$–approach''' without previous iteration $\underline{(I = 0)}$. |
| + | |type="{}"} | ||
| + | $L_{\rm E}(1) \ = \ ${ -0.412--0.388 } | ||
| + | $L_{\rm E}(2) \ = \ ${ -1.03--0.97 } | ||
| + | $L_{\rm E}(3) \ = \ ${ 0.4 3% } | ||
| + | |||
| + | {What are the a-posteriori $L$–values $L_i = L_{\rm APP} (i)$ for the first iteration $\underline{(I = 1)}$? | ||
| + | |type="{}"} | ||
| + | $L_1 \ = \ ${ 0.6 3% } | ||
| + | $L_2 \ = \ ${ -0.618--0.582 } | ||
| + | $L_3 \ = \ ${ -0.618--0.582 } | ||
| + | |||
| + | {Which of the following statements are true for $\underline{L} = (+1.0, +0.4, -1.0)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + Hard decision after $I = 1$ leads to the code word $\underline{x}_1 = (+1, -1, -1)$. |
| − | - | + | + This does not change after further iterations. |
| + | - Further iterations do not increase the reliability for $\underline{x}_1$ . | ||
| − | { | + | {Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.4)$? |
| − | |type="{}"} | + | |type="[]"} |
| − | $ | + | + The iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. |
| + | - The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | ||
| + | + Hard decision also returns this result for $I \ge 1$. | ||
| + | |||
| + | {Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.8)$? | ||
| + | |type="[]"} | ||
| + | - The iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. | ||
| + | + The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | ||
| + | + Hard decision also returns this result for $I \ge 1$. | ||
| + | |||
| + | {Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.6)$? | ||
| + | |type="[]"} | ||
| + | - Iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. | ||
| + | - The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | ||
| + | + The iterative decoding does not lead to the result here. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | [[File:P_ID3027__KC_A_4_5a_v2.png|right|frame|Results for $\underline{L}=(+1.0, +0.4, –1.0)$]] |
| − | '''(2)''' | + | '''(1)''' According to the second $L_{\rm E}(i)$ approach holds: |
| − | '''(3)''' | + | :$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$ |
| − | '''(4)''' | + | :$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4$$ |
| − | '''(5)''' | + | :$$\Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$ |
| + | |||
| + | *In the same way you get: | ||
| + | :$$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, $$ | ||
| + | :$$L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' The a-posteriori $L$–values at the beginning of the first iteration $(I = 1)$ are the sum | ||
| + | *of the previous $L$–values $($for $I = 0$) | ||
| + | *and the extrinsic values calculated in subtask '''(1)''': | ||
| + | :$$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$ | ||
| + | :$$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$ | ||
| + | :$$L_3 = L_{\rm APP}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (-1.0) + 0.4\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' As can be seen from the above table, the <u>solutions 1 and 2</u> are correct in contrast to answer 3: | ||
| + | *With each new iteration, the magnitudes of $L(1), \ L(2)$ and $L(3)$ become significantly larger. | ||
| + | |||
| + | |||
| + | [[File:P_ID3030__KC_A_4_5d_v2.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.4)$]] | ||
| + | <br><br> | ||
| + | '''(4)''' As can be seen from the adjacent table, | ||
| + | the <u>answers 1 and 3</u> are correct: | ||
| + | *So the decision is made for the code word $\underline{x}_0 = (+1, +1, +1)$. | ||
| + | |||
| + | *From $I = 1$ this would also be the decision of "hard decision". | ||
| + | <br clear=all> | ||
| + | [[File:P_ID3028__KC_A_4_5e_v2.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.8)$]] | ||
| + | '''(5)''' Correct are the <u>answers 2 and 3</u>: | ||
| + | *Because of $|L(3)| > |L(1)|$ the following is valid for $I /ge 1$: $L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | L_3 < 0 \hspace{0.05cm}.$ | ||
| + | |||
| + | *From this iteration loop, hard decision returns the code word $\underline{x}_2 = (-1, +1, -1)$. | ||
| + | <br clear=all> | ||
| + | [[File: P_ID3029__KC_A_4_5f_v1.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.6)$]] | ||
| + | '''(6)''' Correct is the <u>proposed solution 3</u>: | ||
| + | *The adjacent table shows that under the condition $|L(1)| = |L(3)|$, starting from the iteration loop $I = 1$, all extrinsic $L$–values are zero. | ||
| + | |||
| + | *Thus, the a-posteriori $L$– values remain constantly equal to $\underline{L} = (0., +0.4, 0.)$ even for $I > 1$, which cannot be assigned to any code word. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 106: | Line 193: | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^4.1 Soft–in Soft–out Decoder^]] |
Latest revision as of 16:06, 4 December 2022
We assume as in the "theory section" the "single parity–check code" $\rm SPC \, (3, \, 2, \, 2)$.
The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} \{ \underline{x}_0,\hspace{0.05cm} \underline{x}_1,\hspace{0.05cm} \underline{x}_2,\hspace{0.05cm} \underline{x}_3\}$ with
- $$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$
- $$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$
In the exercise we mostly use the second (bipolar) representation of the code symbols:
- $$x_i ∈ \{+1, -1\}.$$
Note:
- It is not that the $\rm SPC \, (3, \, 2, \, 2)$ would be of much practical interest, since, for example, in "hard decision" because of $d_{\rm min} = 2$ only one error can be detected and none can be corrected.
- However, the code is well suited for demonstration purposes because of the manageable effort involved.
- With "iterative symbol-wise decoding" one can also correct one error.
- In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$
- Here $\underline{x}^{(-1)}$ denotes all symbols except $x_i$ and is thus a vector of length $n - 1 = 2$.
⇒ As the »first $L_{\rm E}(i)$ approach« we refer to the approach corresponding to the equations
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$
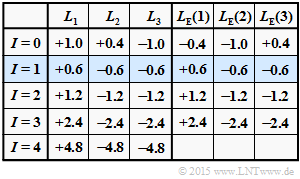
(1) This $L_{\rm E}(i)$ approach underlies the results table above $($red entries$)$, assuming the following a-posteriori $L$–values:
- $$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} L_1 = +1.0\hspace{0.05cm},\hspace{0.15cm} L_2 = +0.4\hspace{0.05cm},\hspace{0.15cm} L_3 = -1.0\hspace{0.05cm}.$$
(2) The extrinsic $L$–values for the zeroth iteration result in $($derivation in $\text{Exercise 4.5Z})$:
- $$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$
(3) The a-posteriori $L$–values at the beginning of the first iteration are thus
- $$\underline{L_{\rm APP} }^{(I=1)} = \underline{L_{\rm APP} }^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) \hspace{0.05cm} . $$
(4) From this, the new extrinsic $L$–values for the iteration loop $I = 1$ are as follows:
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$
Further, one can see from the above table:
- A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$ code word.
- But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$.
- Also in later graphs, the rows with correct hard decisions for the first time are highlighted in blue.
- Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general.
Besides, in this exercise we consider a »second $L_{\rm E}(i)$ approach«, which is given here for the example of the first symbol $(i = 1)$:
- $${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},$$
- $$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$
This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better $($larger$)$ the input log likelihood ratio is completely disregarded.
Let us consider two examples for this:
(1) For $L_2 = 1.0$ and $L_3 = 5.0$ we get
- after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$
(2) On the other hand one obtains for $L_2 = L_3 = 1.0$
- according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$
One can see the clear discrepancy between the two approaches. The second approach $($approximation$)$ is clearly more positive than the first $($correct$)$ approach. However, it is actually only important that the iterations lead to the desired decoding result.
Hints:
- The exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Referred to in particular "Calculation of extrinsic log likelihood ratios".
- Only the second solution approach is treated here.
- For the first solution approach we refer to $\text{Exercise 4.5Z}$ .
Questions
Solution
(1) According to the second $L_{\rm E}(i)$ approach holds:
- $${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$
- $$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4$$
- $$\Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$
- In the same way you get:
- $$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, $$
- $$L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$
(2) The a-posteriori $L$–values at the beginning of the first iteration $(I = 1)$ are the sum
- of the previous $L$–values $($for $I = 0$)
- and the extrinsic values calculated in subtask (1):
- $$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$
- $$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$
- $$L_3 = L_{\rm APP}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (-1.0) + 0.4\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm}.$$
(3) As can be seen from the above table, the solutions 1 and 2 are correct in contrast to answer 3:
- With each new iteration, the magnitudes of $L(1), \ L(2)$ and $L(3)$ become significantly larger.
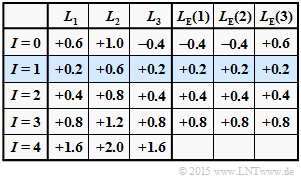
(4) As can be seen from the adjacent table,
the answers 1 and 3 are correct:
- So the decision is made for the code word $\underline{x}_0 = (+1, +1, +1)$.
- From $I = 1$ this would also be the decision of "hard decision".
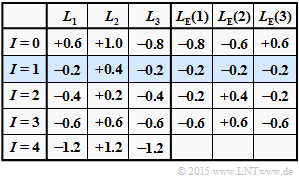
(5) Correct are the answers 2 and 3:
- Because of $|L(3)| > |L(1)|$ the following is valid for $I /ge 1$: $L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} L_3 < 0 \hspace{0.05cm}.$
- From this iteration loop, hard decision returns the code word $\underline{x}_2 = (-1, +1, -1)$.
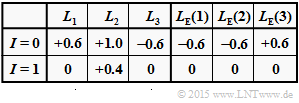
(6) Correct is the proposed solution 3:
- The adjacent table shows that under the condition $|L(1)| = |L(3)|$, starting from the iteration loop $I = 1$, all extrinsic $L$–values are zero.
- Thus, the a-posteriori $L$– values remain constantly equal to $\underline{L} = (0., +0.4, 0.)$ even for $I > 1$, which cannot be assigned to any code word.