Difference between revisions of "Aufgaben:Exercise 2.1: Linear? Or Non-Linear?"
From LNTwww
m (Guenter verschob die Seite 2.1 Linear? - Nichtlinear? nach Aufgabe 2.1: Linear? - Nichtlinear?) |
|||
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions}} |
| − | }} | ||
| − | [[File:P_ID879__LZI_A_2_1.png|right| | + | [[File:P_ID879__LZI_A_2_1.png|right|frame|Interconnected system]] |
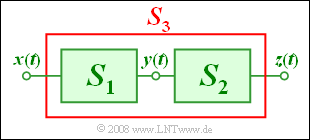
| − | + | We consider the sketched arrangement with input $x(t)$ and output $z(t)$: | |
| − | * | + | *The system $S_1$ is describable by the following equation: |
:$$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$ | :$$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$ | ||
| − | * | + | *Nothing else is known about the system $S_2$ with input $y(t)$ and output $z(t)$ . |
| − | * | + | *The system $S_3$ is the interconnection of $S_1$ and $S_2$. |
| − | An | + | An oscillation with frequency $f_0 = 5 \ \rm kHz$ is applied to the input: |
:$$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$ | :$$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$ | ||
| − | + | Hence, at the output of the overall system $S_3$ the following is obtained: | |
:$$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$ | :$$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Please note:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|Classification of the Distortions]]. | ||
| + | |||
| + | *The following trigonometric relation is given: | ||
| + | :$$\cos^2(\alpha) = {1}/{2} \cdot \big[ 1 + \cos(2\alpha)\big].$$ | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the signal $y(t)$? What is the signal value at time zero? |
|type="{}"} | |type="{}"} | ||
| − | $y(t = 0) \ $ | + | $y(t = 0) \ = \ $ { 6 1% } $\ \rm V$ |
| − | { | + | {What correct conclusions could be drawn by an observer who only knows the signals $x(t)$ and $z(t)$ but not the structure of $S_3$? |
|type="[]"} | |type="[]"} | ||
| − | - $S_3$ | + | - $S_3$ is an ideal system. |
| − | + $S_3$ | + | + $S_3$ is a distortion-free system. |
| − | + $S_3$ | + | + $S_3$ is a linearly distorting system. |
| − | - $S_3$ | + | - $S_3$ is a non-linearly distorting system. |
| − | { | + | {What conclusions would the observer have to draw if all the information from the information section is known to them? |
|type="[]"} | |type="[]"} | ||
| − | - $S_2$ | + | - $S_2$ is a distortion-free system. |
| − | + $S_2$ | + | + $S_2$ is a linearly distorting system. |
| − | - $S_2$ | + | - $S_2$ is a non-linearly distorting system. |
| − | { | + | {What signal $z(t)$ could arise as a result with the input frequency $f_0 = 10 \ \rm kHz$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The signal $z(t)$ is zero for all times. |
| − | - | + | - A signal of the form $z(t) = A \cdot {\rm cos}(2\pi \cdot 10 \ {\rm kHz} \cdot t ) ,$ with $A \ne 0.$ |
| − | + | + | + A signal of the form $z(t) = A \cdot {\rm cos}(2\pi \cdot 20 \ {\rm kHz} \cdot t ) ,$ with $A \ne 0.$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The following holds due to the characteristic curve with linear and quadratic components: |
| − | $$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, | + | :$$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, |
\rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 | \rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 | ||
| − | t ) = {2 \, \rm V} \cdot \ | + | t ) = {2 \, \rm V} \cdot \big[ 1 + {\rm cos}(2\pi \cdot f_0 \cdot t |
| − | ) +{\rm cos}(2\pi \cdot 2f_0 \cdot t ) \ | + | ) +{\rm cos}(2\pi \cdot 2f_0 \cdot t ) \big].$$ |
| − | + | *Therefore, the <u>signal value 6 V</u> occurs at time $t= 0$ . | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(2)''' <u>Alternatives 2 snd 3</u> are possible: |
| − | $ | + | *An ideal system is out of the question because of $z(t) ≠ x(t)$ . |
| − | + | *With only one input frequency $(f_0 = 5 \ \rm kHz)$ in the test signal it is not possible to make a statement about whether a second frequency component with $f \ne f_0$ would also be attenuated by $\alpha = 0.5$ and delayed by $\tau = T_0/4 = 50 \ µ\rm s$ . | |
| − | + | *If for the second frequency component $\alpha = 0.5$ and $\tau = T_0/4 = 50 \ µ \rm s$ arose as a result, a ''distortion-free system'' could exist. | |
| + | *If for the second frequency component $\alpha \ne 0.5$ and/or $\tau \ne T_0/4$ arose as a result, then the system would be ''linearly distorting''. | ||
| + | *The last alternative would have to be logically denied – although partially true – by the observer. | ||
| − | + | ||
| − | $$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm | + | |
| + | '''(3)''' <u>Approach 2</u> is correct: | ||
| + | *The observer would realise that $S_2$ is a linearly distorting system. | ||
| + | *For a distortion-free system, $z(t)$ would additionally have to include a direct (DC) component and a $10 \ \rm kHz$–component, | ||
| + | *for a non-linearly distorting system, even larger frequency components $($at multiples of $10 \ \rm kHz)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' In this case the following would hold: | ||
| + | :$$y(t) = {2 \, \rm V} \cdot \big[ 1 + {\rm cos}(2\pi \cdot 10 \ {\rm kHz} \cdot t | ||
| + | ) +{\rm cos}(2\pi \cdot 20 \ {\rm kHz} \cdot t ) \big].$$ | ||
| + | *That is: $Y(f)$ would have spectral lines at $f = 0$, $10 \ \rm kHz$ and $20 \ \rm kHz$ . | ||
| + | |||
| + | *However, the measurement described in the information section with $f_0 = 5 \ \rm kHz$ has shown that $H_2(f = 0) = H_2(f = 10 \ {\rm kHz}) = 0$ must hold. | ||
| + | *The only possible signal form is therefore | ||
| + | :$$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm | ||
cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$ | cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$ | ||
| − | + | *So, <u>approaches 1 and 3</u> are possible depending on whether the system $S_2$ suppresses or passes the frequency $20 \ {\rm kHz}$ . | |
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^2.1 Classification of the Distortions^]] |
Latest revision as of 13:45, 17 November 2022
We consider the sketched arrangement with input $x(t)$ and output $z(t)$:
- The system $S_1$ is describable by the following equation:
- $$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$
- Nothing else is known about the system $S_2$ with input $y(t)$ and output $z(t)$ .
- The system $S_3$ is the interconnection of $S_1$ and $S_2$.
An oscillation with frequency $f_0 = 5 \ \rm kHz$ is applied to the input:
- $$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$
Hence, at the output of the overall system $S_3$ the following is obtained:
- $$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$
Please note:
- The exercise belongs to the chapter Classification of the Distortions.
- The following trigonometric relation is given:
- $$\cos^2(\alpha) = {1}/{2} \cdot \big[ 1 + \cos(2\alpha)\big].$$
Questions
Solution
(1) The following holds due to the characteristic curve with linear and quadratic components:
- $$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, \rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 t ) = {2 \, \rm V} \cdot \big[ 1 + {\rm cos}(2\pi \cdot f_0 \cdot t ) +{\rm cos}(2\pi \cdot 2f_0 \cdot t ) \big].$$
- Therefore, the signal value 6 V occurs at time $t= 0$ .
(2) Alternatives 2 snd 3 are possible:
- An ideal system is out of the question because of $z(t) ≠ x(t)$ .
- With only one input frequency $(f_0 = 5 \ \rm kHz)$ in the test signal it is not possible to make a statement about whether a second frequency component with $f \ne f_0$ would also be attenuated by $\alpha = 0.5$ and delayed by $\tau = T_0/4 = 50 \ µ\rm s$ .
- If for the second frequency component $\alpha = 0.5$ and $\tau = T_0/4 = 50 \ µ \rm s$ arose as a result, a distortion-free system could exist.
- If for the second frequency component $\alpha \ne 0.5$ and/or $\tau \ne T_0/4$ arose as a result, then the system would be linearly distorting.
- The last alternative would have to be logically denied – although partially true – by the observer.
(3) Approach 2 is correct:
- The observer would realise that $S_2$ is a linearly distorting system.
- For a distortion-free system, $z(t)$ would additionally have to include a direct (DC) component and a $10 \ \rm kHz$–component,
- for a non-linearly distorting system, even larger frequency components $($at multiples of $10 \ \rm kHz)$.
(4) In this case the following would hold:
- $$y(t) = {2 \, \rm V} \cdot \big[ 1 + {\rm cos}(2\pi \cdot 10 \ {\rm kHz} \cdot t ) +{\rm cos}(2\pi \cdot 20 \ {\rm kHz} \cdot t ) \big].$$
- That is: $Y(f)$ would have spectral lines at $f = 0$, $10 \ \rm kHz$ and $20 \ \rm kHz$ .
- However, the measurement described in the information section with $f_0 = 5 \ \rm kHz$ has shown that $H_2(f = 0) = H_2(f = 10 \ {\rm kHz}) = 0$ must hold.
- The only possible signal form is therefore
- $$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$
- So, approaches 1 and 3 are possible depending on whether the system $S_2$ suppresses or passes the frequency $20 \ {\rm kHz}$ .