Difference between revisions of "Aufgaben:Exercise 3.6Z: Two Imaginary Poles"
From LNTwww
m (Guenter verschob die Seite 3.6Z Zwei imaginäre Pole nach Aufgabe 3.6Z: Zwei imaginäre Pole) |
|||
| (23 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform |
}} | }} | ||
| − | [[File:P_ID1786__LZI_Z_3_6.png|right| | + | [[File:P_ID1786__LZI_Z_3_6.png|right|frame|Two imaginary poles <br>and one zero ]] |
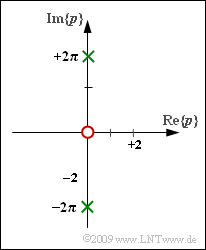
| − | In | + | In this exercise, we consider a causal signal $x(t)$ with the Laplace transform |
| − | $$X_{\rm L}(p) = | + | :$$X_{\rm L}(p) = |
\frac { p} { p^2 + 4 \pi^2}= | \frac { p} { p^2 + 4 \pi^2}= | ||
\frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} | \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | + | corresponding to the graph (one red zero and two green poles). | |
| − | + | *In contrast, the signal $y(t)$ has the Laplace spectral function | |
:$$Y_{\rm L}(p) = | :$$Y_{\rm L}(p) = | ||
\frac { 1} { p^2 + 4 \pi^2} | \frac { 1} { p^2 + 4 \pi^2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | :Thus, the red zero does not belong to $Y_{\rm L}(p)$. | |
| − | + | *Finally, the signal $z(t)$ with the Laplace tansform | |
| − | $$Z_{\rm L}(p) = | + | :$$Z_{\rm L}(p) = |
\frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | + | :is considered, in particular the limiting case for $\beta → 0$. | |
| − | + | ||
| − | * | + | |
| − | * | + | |
| − | + | ||
| − | * | + | Please note: |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. |
| − | :$$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p | + | *The frequency variable $p$ is normalized such that time $t$ is in microseconds after applying the residue theorem. |
| − | \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \it | + | *A result $t = 1$ is thus to be interpreted as $t = T$ with $T = 1 \ \rm µ s$ . |
| + | *The [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] is as follows using the example of the function $X_{\rm L}(p)$ with two simple poles at $ \pm {\rm j} \cdot \beta$: | ||
| + | :$$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p\hspace{0.05cm} \cdot | ||
| + | \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it | ||
\beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p | \beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p | ||
| − | \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \it | + | \hspace{0.05cm} \cdot\hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it |
\beta}} | \beta}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the signal $x(t)$. Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | + $x(t)$ | + | + $x(t)$ is a causal cosine signal. |
| − | - $x(t)$ | + | - $x(t)$ is a causal sinusoidal signal. |
| − | + | + | + The amplitude of $x(t)$ is $1$. |
| − | + | + | + The period of $x(t)$ is $T = 1 \ \rm µ s$. |
| − | { | + | {Compute the signal $y(t)$. Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - $y(t)$ | + | - $y(t)$ is a causal cosine signal. |
| − | + $y(t)$ | + | + $y(t)$ is a causal sinusoidal signal. |
| − | - | + | - The amplitude of $y(t)$ is $1$. |
| − | + | + | + The period of $y(t)$ is $T = 1 \ \rm µ s$. |
| − | { | + | {Which statements are true for the signal $z(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For $ \beta > 0$, $z(t)$ is cosine-shaped. |
| − | - | + | - For $ \beta > 0$, $z(t)$ is sinusoidal. |
| − | + | + | + The limiting case $\beta → 0$ results in the step function $\gamma(t)$. |
| Line 66: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>suggested solutions 1, 3 and 4</u> are correct: |
| − | $$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | + | *The following is obtained for signal $x(t)$ for positive times by applying the residue theorem: |
| − | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | + | :$$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} |
| + | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t}\}= | ||
\frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | \frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | ||
| − | \hspace{0.05cm}t} | + | \hspace{0.05cm}\cdot \hspace{0.05cm}t} |
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | ||
\frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,$$ | \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,$$ | ||
| − | $$ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} | + | :$$ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} |
| − | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= | + | \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\}= |
\frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | \frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p | ||
| − | \hspace{0.05cm}t} | + | \hspace{0.05cm}\cdot \hspace{0.05cm}t} |
\bigg |_{p \hspace{0.05cm}= -{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | \bigg |_{p \hspace{0.05cm}= -{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= | ||
\frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} | \frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | $$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = | + | :$$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = |
{1}/{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | {1}/{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | ||
t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | ||
t}\right ] = \cos(2\pi t) | t}\right ] = \cos(2\pi t) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | |||
| − | '''(2)''' | + | |
| − | $$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi | + | '''(2)''' The <u>suggested solutions 2 and 4</u> are correct: |
| + | *In principle, this subtask could be solved in the same way as subtask '''(1)'''. | ||
| + | *However, the integration theorem can also be used. | ||
| + | *This says among other things that multiplication by $1/p$ in the spectral domain corresponds to integration in the time domain: | ||
| + | :$$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi | ||
\tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t) | \tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | |||
| − | + | Please note: The causal cosine signal $x(t)$ and the causal sine signal $y(t)$ are shown on the information page of [[Aufgaben:Exercise_3.6:_Transient_Behavior|Exercise 3.6]] as $c_{\rm K}(t)$ and $s_{\rm K}(t)$, respectively. | |
| − | |||
| − | + | '''(3)''' The <u>suggested solutions 1 and 3</u> are correct: | |
| − | $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} | + | *A comparison with the computation of $x(t)$ shows that $z(t) = \cos (\beta \cdot t)$ holds for $t \ge 0$ and $z(t) = 0$ for $t < 0$. |
| + | *The limit process for $\beta → 0$ thus results in the step function $\gamma(t)$. | ||
| + | *The same result is obtained by consideration in the spectral domain: | ||
| + | :$$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
z(t) = \gamma(t) | z(t) = \gamma(t) | ||
| Line 110: | Line 118: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^3.3 Inverse Laplace Transform^]] |
Latest revision as of 17:33, 9 December 2021
In this exercise, we consider a causal signal $x(t)$ with the Laplace transform
- $$X_{\rm L}(p) = \frac { p} { p^2 + 4 \pi^2}= \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} \hspace{0.05cm}$$
corresponding to the graph (one red zero and two green poles).
- In contrast, the signal $y(t)$ has the Laplace spectral function
- $$Y_{\rm L}(p) = \frac { 1} { p^2 + 4 \pi^2} \hspace{0.05cm}.$$
- Thus, the red zero does not belong to $Y_{\rm L}(p)$.
- Finally, the signal $z(t)$ with the Laplace tansform
- $$Z_{\rm L}(p) = \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} \hspace{0.05cm}$$
- is considered, in particular the limiting case for $\beta → 0$.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
- The frequency variable $p$ is normalized such that time $t$ is in microseconds after applying the residue theorem.
- A result $t = 1$ is thus to be interpreted as $t = T$ with $T = 1 \ \rm µ s$ .
- The residue theorem is as follows using the example of the function $X_{\rm L}(p)$ with two simple poles at $ \pm {\rm j} \cdot \beta$:
- $$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p\hspace{0.05cm} \cdot \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it \beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm} \cdot\hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it \beta}} \hspace{0.05cm}.$$
Questions
Solution
(1) The suggested solutions 1, 3 and 4 are correct:
- The following is obtained for signal $x(t)$ for positive times by applying the residue theorem:
- $$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t}\}= \frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,$$
- $$ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\}= \frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= -{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} \hspace{0.05cm} .$$
- $$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = {1}/{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\right ] = \cos(2\pi t) \hspace{0.05cm} .$$
(2) The suggested solutions 2 and 4 are correct:
- In principle, this subtask could be solved in the same way as subtask (1).
- However, the integration theorem can also be used.
- This says among other things that multiplication by $1/p$ in the spectral domain corresponds to integration in the time domain:
- $$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi \tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t) \hspace{0.05cm} .$$
Please note: The causal cosine signal $x(t)$ and the causal sine signal $y(t)$ are shown on the information page of Exercise 3.6 as $c_{\rm K}(t)$ and $s_{\rm K}(t)$, respectively.
(3) The suggested solutions 1 and 3 are correct:
- A comparison with the computation of $x(t)$ shows that $z(t) = \cos (\beta \cdot t)$ holds for $t \ge 0$ and $z(t) = 0$ for $t < 0$.
- The limit process for $\beta → 0$ thus results in the step function $\gamma(t)$.
- The same result is obtained by consideration in the spectral domain:
- $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z(t) = \gamma(t) \hspace{0.05cm} .$$