Difference between revisions of "Aufgaben:Exercise 1.2: Bit Error Rate"
m (Guenter verschob die Seite 1.2 Bitfehlerquote (BER) nach Aufgabe 1.2: Bitfehlerquote (BER)) |
|||
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission |
}} | }} | ||
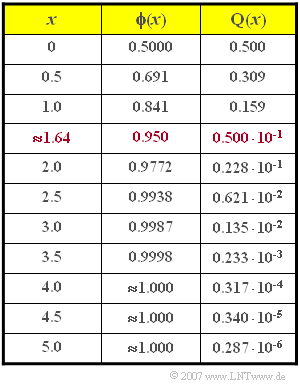
| − | [[File:P_ID1264__Dig_A_1_2.png|right|frame| | + | [[File:P_ID1264__Dig_A_1_2.png|right|frame|Table of two Gaussian error functions]] |
| − | + | It is known from a digital transmission system that it can be approximated by a | |
| − | BSC& | + | BSC model ("Binary Symmetrical Channel") with error probability $p$. |
| − | + | For verification, the bit error rate is to be determined by comparing the sink symbol sequence $ \langle v_\nu \rangle $ with the source symbol sequence | |
| − | $ \langle q_\nu \rangle $ | + | $ \langle q_\nu \rangle $ and finding the error sequence $ \langle e_\nu \rangle $. Thereby holds: |
| − | $$e_\nu = \left\{ \begin{array}{c} 0 \\ | + | :$$e_\nu = \left\{ \begin{array}{c} 0 \\ |
1 \\ \end{array} \right.\quad | 1 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}} |
| − | \\ {\rm{ | + | \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |
v_\nu = q_\nu \hspace{0.05cm}, \\ | v_\nu = q_\nu \hspace{0.05cm}, \\ | ||
v_\nu \ne q_\nu . \\ | v_\nu \ne q_\nu . \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | The bit error rate is an approximation for the bit error probability $p$: | |
:$${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$ | :$${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$ | ||
| − | + | The larger the simulation parameter $N$ is chosen, the more accurate is this approximation. | |
| − | + | From [[Aufgaben:Exercise_3.7:_Bit_Error_Rate_(BER)|"Exercise 3.7"]] in the book "Stochastic Signal Theory" it is known that the random variable "BER" is actually binomially distributed, but can be approximated with good approximation by a (discrete) Gaussian distribution with mean $p$ and standard deviation $\sigma$: | |
:$$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$ | :$$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission|"Error Probability for Baseband Transmission"]]. | ||
| + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|"Gaussian Distributed Random Variables"]] in the book "Stochastic Signal Theory". | ||
| + | *In the table some values of the Gaussian error functions ${\rm \phi}(x)$ and ${\rm Q}(x)$ are given. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What does $\rm BER$ describe in terms of probability theory? |
|type="[]"} | |type="[]"} | ||
| − | - $\rm BER$ | + | - $\rm BER$ is a probability. |
| − | + $\rm BER$ | + | + $\rm BER$ is a relative frequency. |
| − | - | + | - If $N$ is sufficiently large, $\rm BER$ coincides <b>exactly</b> with $p$. |
| − | { | + | {Calculate the standard deviation $\sigma$ for $N = 10^6$ and $p = 10^{-2}$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma \ =\ $ { 1 3% } $\ \cdot 10^{ -4 }\ $ |
| − | { | + | {What is the probability that the bit error rate differs in magnitude by more than $5\%$ from the probability $\underline{p = 10^{-2}}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}(|{\rm BER} – p| > 0.05 · p) \ =\ ${ 0.00574 10% } $\ \cdot 10^{ -4 }\ $ |
| − | { | + | {What is the same probability with $\underline{p = 10^{-4}}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}(|{\rm BER} – p| > 0.05 · p) \ =\ $ { 0.618 3% } |
| − | { | + | {What would be the minimum size of $N$ for $\underline{p = 10^{-4}}$ to be no more than $10\%$ outside the interval of $0.95 \cdot 10^{-4}$ ... $1.05 \cdot 10^{-4}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_{\rm min} \ =\ $ { 10.8 10% } $\ \cdot 10^{ 6 }\ $ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Only the second statement</u> is correct: |
| − | *$\rm BER$ | + | *$\rm BER$ is the quotient of the number $n_{\rm B}$ of detected symbol errors and the number $N$ of all simulated symbols and thus actually a relative frequency. |
| − | * | + | *The probability that ${\rm BER} = p$ is always exactly zero, since $\rm BER$ is a continuous random variable. |
| − | * | + | *However, the probability that $\rm BER$ lies in a narrow interval around $p$ increases as $N$ increases. |
| − | '''(2)''' | + | |
| + | '''(2)''' The standard deviation of the Gaussian random variable $\rm BER$ with $N = 10^6$ and $p = 10^{-2}$ is given by | ||
:$$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | :$$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| − | $0.95 \cdot p$ ... $1.05 \cdot p$ | + | '''(3)''' The probability that the $\rm BER$ takes a value outside the range |
| + | $0.95 \cdot p$ ... $1.05 \cdot p$ is obtained with $\varepsilon = 5 \cdot 10^{-4}$ $(p = 10^{-2})$ as follows. | ||
:$${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) | :$${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) | ||
= {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) | = {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) | ||
| Line 81: | Line 86: | ||
= 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-4}}{10^{-4}} \right) = 2 \cdot 0.287 \cdot 10^{-6}\hspace{0.1cm}\underline {= 0.00574 \cdot 10^{-4}}\hspace{0.05cm}.$$ | = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-4}}{10^{-4}} \right) = 2 \cdot 0.287 \cdot 10^{-6}\hspace{0.1cm}\underline {= 0.00574 \cdot 10^{-4}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| + | '''(4)''' With $p = 10^{-4}$, the comparable probability is: | ||
:$${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) | :$${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) | ||
= 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} | = 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} | ||
\right);\hspace{0.5cm} | \right);\hspace{0.5cm} | ||
| − | \text{ | + | \text{with}\hspace{0.5cm}\sigma \approx \sqrt{{ p}/{N}}= |
10^{-5}\hspace{0.05cm}, \hspace{0.3cm}\varepsilon = 5 \cdot | 10^{-5}\hspace{0.05cm}, \hspace{0.3cm}\varepsilon = 5 \cdot | ||
10^{-6}\text{:}$$ | 10^{-6}\text{:}$$ | ||
| Line 91: | Line 97: | ||
= 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-6}}{10^{-5}} \right) = 2 \cdot 0.309 \hspace{0.1cm}\underline {= 0.618} \hspace{0.05cm}.$$ | = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-6}}{10^{-5}} \right) = 2 \cdot 0.309 \hspace{0.1cm}\underline {= 0.618} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | |
| + | '''(5)''' This condition can be formulated with $\varepsilon = 5 \cdot 10^{-6}$ as follows: | ||
:$${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 | {\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 | ||
| Line 106: | Line 113: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.2 BER for Baseband Systems^]] |
Latest revision as of 15:51, 9 May 2022
It is known from a digital transmission system that it can be approximated by a BSC model ("Binary Symmetrical Channel") with error probability $p$.
For verification, the bit error rate is to be determined by comparing the sink symbol sequence $ \langle v_\nu \rangle $ with the source symbol sequence $ \langle q_\nu \rangle $ and finding the error sequence $ \langle e_\nu \rangle $. Thereby holds:
- $$e_\nu = \left\{ \begin{array}{c} 0 \\ 1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} v_\nu = q_\nu \hspace{0.05cm}, \\ v_\nu \ne q_\nu . \\ \end{array}$$
The bit error rate is an approximation for the bit error probability $p$:
- $${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$
The larger the simulation parameter $N$ is chosen, the more accurate is this approximation.
From "Exercise 3.7" in the book "Stochastic Signal Theory" it is known that the random variable "BER" is actually binomially distributed, but can be approximated with good approximation by a (discrete) Gaussian distribution with mean $p$ and standard deviation $\sigma$:
- $$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$
Notes:
- The exercise belongs to the chapter "Error Probability for Baseband Transmission".
- Reference is also made to the chapter "Gaussian Distributed Random Variables" in the book "Stochastic Signal Theory".
- In the table some values of the Gaussian error functions ${\rm \phi}(x)$ and ${\rm Q}(x)$ are given.
Questions
Solution
- $\rm BER$ is the quotient of the number $n_{\rm B}$ of detected symbol errors and the number $N$ of all simulated symbols and thus actually a relative frequency.
- The probability that ${\rm BER} = p$ is always exactly zero, since $\rm BER$ is a continuous random variable.
- However, the probability that $\rm BER$ lies in a narrow interval around $p$ increases as $N$ increases.
(2) The standard deviation of the Gaussian random variable $\rm BER$ with $N = 10^6$ and $p = 10^{-2}$ is given by
- $$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$
(3) The probability that the $\rm BER$ takes a value outside the range
$0.95 \cdot p$ ... $1.05 \cdot p$ is obtained with $\varepsilon = 5 \cdot 10^{-4}$ $(p = 10^{-2})$ as follows.
- $${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) = {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) = {\rm Q} \left({\varepsilon}/{\sigma} \right)$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - p| > \varepsilon \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-4}}{10^{-4}} \right) = 2 \cdot 0.287 \cdot 10^{-6}\hspace{0.1cm}\underline {= 0.00574 \cdot 10^{-4}}\hspace{0.05cm}.$$
(4) With $p = 10^{-4}$, the comparable probability is:
- $${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} \right);\hspace{0.5cm} \text{with}\hspace{0.5cm}\sigma \approx \sqrt{{ p}/{N}}= 10^{-5}\hspace{0.05cm}, \hspace{0.3cm}\varepsilon = 5 \cdot 10^{-6}\text{:}$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-6}}{10^{-5}} \right) = 2 \cdot 0.309 \hspace{0.1cm}\underline {= 0.618} \hspace{0.05cm}.$$
(5) This condition can be formulated with $\varepsilon = 5 \cdot 10^{-6}$ as follows:
- $${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\varepsilon^2}{\sigma^2}\approx \frac{\varepsilon^2 \cdot N}{p}> 1.64^2 = 2.69$$
- $$\Rightarrow \hspace{0.3cm} N > \frac{2.69 \cdot p}{\varepsilon^2}= \frac{2.69 \cdot 10^{-4}}{25 \cdot10^{-12}}\hspace{0.1cm}\underline {\approx 10.8 \cdot 10^{6}}\hspace{0.05cm}.$$