Difference between revisions of "Aufgaben:Exercise 3.6: Adaptive Multi Rate Codec"
m (Guenter verschob die Seite 3.6 Adaptive Multi–Rate Codec nach Aufgabe 3.6: Adaptive Multi–Rate Codec) |
|||
| (23 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Voice_Coding |
}} | }} | ||
| − | [[File: | + | [[File:En_Bei_A_3_6.png|right|frame|Tracks of the AMR codec]] |
| − | + | In the late 1990s, a very flexible, adaptive speech codec was developed and standardized in the form of $\rm AMR$ codec. This provides a total of eight different modes with data rates between $4.75 \ \rm kbit/s$ and $12.2 \ \rm kbit/s$. | |
| − | + | The AMR codec, like the full rate codec $\rm (FRC)$ discussed in [[Aufgaben:Exercise_3.5:_GSM_Full_Rate_Vocoder|$\text{Exercise 3.5}$]], includes both a short-term prediction $\rm (LPC)$ and a long-term prediction $\rm (LTP)$. However, these two components are realized differently from FRC. | |
| − | + | The main difference between AMR and FRC is the encoding of the residual signal $($after LPC and LTP$)$: | |
| + | #Instead of "Regular Pulse Excitation" $\rm (RPE)$, here the "Algebraic Code Excitation Linear Prediction" $\rm (ACELP)$ is used. | ||
| + | #From the fixed code book $\rm (FCB)$, for each subframe of $5 \ \rm ms$ duration, the "FCB pulse" and the "FCB gain" that best match the residual signal $($for which the mean square error of the difference signal becomes minimum$)$ is selected. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Each entry in the fixed code book identifies a pulse where exactly $10$ of $40$ positions are occupied by $\pm1$. | ||
| − | In | + | In this regard it should be noted: |
| − | + | *The pulse is divided into five tracks with eight possible positions each, where track $1$ contains the positions $1,\ 6,\ 11$, ... , $36$ of the subframe and track $5$ describes the positions $5,\ 10,\ 15$, ... , $40$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *In each track there are exactly two values $\pm1$, while all the other six values are zero. | |
| + | *The two $±1$-positions are each assigned three bits – i.e. encoded with "$000$", ... , "$111$". | ||
| − | + | *Another bit is used for the "sign of the first-mentioned pulse", where a "$1$" indicates a positive sign and a "$0$" a negative sign. | |
| − | + | *If the pulse position of the second pulse is greater than that of the first pulse, the second pulse has the same sign as the first, otherwise the opposite. | |
| + | *Thus, seven bits per track are transmitted to the receiver, plus five bits for the so-called "FCB amplification''. | ||
| − | ''' | + | |
| − | === | + | In the diagram, the $35$ bits describing an FCB pulse are given as an example: |
| + | |||
| + | ⇒ '''Track 1''' includes | ||
| + | #a positive pulse $({\rm sign} = 1)$ at position $\big [1$ (first possible position for track 1) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}0$ (bit specification for "000") $= 1\big]$, | ||
| + | #another positive pulse $($since $110 > 000)$ at position $\big [1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.02cm}\text{times}\hspace{0.2cm}6$ (bit specification for " 110") = $31\hspace{0.05cm}\big].$ | ||
| + | |||
| + | |||
| + | '''Track 2''' includes. | ||
| + | #a negative pulse (${\rm sign} = 0$) at position $\big [2$ (first possible position for track 2) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}4$ (bit specification for " 100") $=22\hspace{0.05cm}\big],$ | ||
| + | #a positive pulse $($sign reversal due to $011 > 100)$ at position $\big [2 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}3$ (bit specification for " 011") $=17\hspace{0.05cm}\big].$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <u>Hint:</u> | ||
| + | |||
| + | *This exercise belongs to the chapter [[Examples_of_Communication_Systems/Voice_Coding|"Speech Coding"]]. | ||
| + | |||
| + | *When entering the pulse positions $N_{1}$ denotes the first triple of bits and $N_{2}$ the second. | ||
| + | |||
| + | *For example, for track $2$ one would have to enter the values $N_{1}=-22$ and $N_{2}=+17$. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many bits describe a speech frame $($of duration $20 \ \rm ms)$ in $12.2 \ \rm kbit/s$ mode? |
|type="{}"} | |type="{}"} | ||
| − | $N_{12.2} \ = \ $ { 244 3% } $ \ \rm | + | $N_{12.2} \ = \ $ { 244 3% } $ \ \rm bits$ |
| − | { | + | {How many bits are needed for FCB pulse and gain per frame? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm FCB} \ = \ $ { 160 3% } $ \ \rm | + | $N_{\rm FCB} \ = \ $ { 160 3% } $ \ \rm bits$ |
| − | { | + | { How many bits are left for LPC and LTP? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm LPC/LTP} \ = \ $ { 84 3% } $ \ \rm | + | $N_{\rm LPC/LTP} \ = \ $ { 84 3% } $ \ \rm bits$ |
| − | { | + | {What subframe pulse positions and signs does track $3$ describe? Follow the instructions for input on the information page. |
|type="{}"} | |type="{}"} | ||
$N_{1} \ = \ $ { -8.24--7.76 } | $N_{1} \ = \ $ { -8.24--7.76 } | ||
$N_{2} \ = \ $ { -18.54--17.46 } | $N_{2} \ = \ $ { -18.54--17.46 } | ||
| − | { | + | {What pulse positions including sign describe the track $4$? |
|type="{}"} | |type="{}"} | ||
$N_{1} \ = \ $ { 39 3% } | $N_{1} \ = \ $ { 39 3% } | ||
$N_{2} \ = \ $ { -14.42--13.58 } | $N_{2} \ = \ $ { -14.42--13.58 } | ||
| − | { | + | {What pulse positions including sign describe the track $5$? |
|type="{}"} | |type="{}"} | ||
$N_{1} \ = \ $ { -30.9--29.1 } | $N_{1} \ = \ $ { -30.9--29.1 } | ||
| Line 66: | Line 88: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With the data rate $R_{\rm C} = 12.2 \ \rm kbit/s$, exactly $\underline{244 \ \rm bits}$ results within $20 \ \rm ms$, while e.g. in $4.75 \ \rm kbit/s$ mode only $95 \ \rm bits$ are transmitted. |
| + | |||
| + | |||
| + | '''(2)''' In each subframe, the FCB pulse requires $35 \ \rm bits$ (five tracks of seven bits each) and the FCB gain requires five bits. | ||
| + | |||
| + | *With four subframes, this gives $N_{\rm FCB} \hspace{0.15cm}\underline{= 160 \ \rm bits}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' This leaves the difference from '''(1)''' and '''(2)''', i.e. $N_{\rm LPC/LTP}\hspace{0.15cm} \underline{ = 84\ \rm bits}$. | ||
| + | |||
| − | '''( | + | '''(4)''' The sign bit "$0$" indicates a negative first pulse. |
| + | *Because $001 < 011$, the second pulse has the same sign. | ||
| + | |||
| + | *The two magnitudes result in | ||
| + | :$$|N_1| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 1 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 001)} = 8\hspace{0.05cm}, $$ | ||
| + | :$$ |N_2| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 3 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 011)} = 18\hspace{0.05cm}.$$ | ||
| + | *Therefore, to be entered for the third track is $N_{1}\hspace{0.15cm} \underline{ = -8}$ and $N_{2} \hspace{0.15cm}\underline{ = -18}.$ | ||
| − | |||
| − | '''( | + | '''(5)''' In an analogous way, for track $4$ we obtain the values $N_{1}\hspace{0.15cm} \underline{ = +39}$ and $N_{2}\hspace{0.15cm} \underline{ = -14}$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(6)''' | + | '''(6)''' The fifth track provides $N_{1}\hspace{0.15cm} \underline{ =-30}$ and $N_{2}\hspace{0.15cm} \underline{ = +5}$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 88: | Line 121: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^3.3 Speech Coding^]] |
Latest revision as of 13:58, 25 January 2023
In the late 1990s, a very flexible, adaptive speech codec was developed and standardized in the form of $\rm AMR$ codec. This provides a total of eight different modes with data rates between $4.75 \ \rm kbit/s$ and $12.2 \ \rm kbit/s$.
The AMR codec, like the full rate codec $\rm (FRC)$ discussed in $\text{Exercise 3.5}$, includes both a short-term prediction $\rm (LPC)$ and a long-term prediction $\rm (LTP)$. However, these two components are realized differently from FRC.
The main difference between AMR and FRC is the encoding of the residual signal $($after LPC and LTP$)$:
- Instead of "Regular Pulse Excitation" $\rm (RPE)$, here the "Algebraic Code Excitation Linear Prediction" $\rm (ACELP)$ is used.
- From the fixed code book $\rm (FCB)$, for each subframe of $5 \ \rm ms$ duration, the "FCB pulse" and the "FCB gain" that best match the residual signal $($for which the mean square error of the difference signal becomes minimum$)$ is selected.
Each entry in the fixed code book identifies a pulse where exactly $10$ of $40$ positions are occupied by $\pm1$.
In this regard it should be noted:
- The pulse is divided into five tracks with eight possible positions each, where track $1$ contains the positions $1,\ 6,\ 11$, ... , $36$ of the subframe and track $5$ describes the positions $5,\ 10,\ 15$, ... , $40$.
- In each track there are exactly two values $\pm1$, while all the other six values are zero.
- The two $±1$-positions are each assigned three bits – i.e. encoded with "$000$", ... , "$111$".
- Another bit is used for the "sign of the first-mentioned pulse", where a "$1$" indicates a positive sign and a "$0$" a negative sign.
- If the pulse position of the second pulse is greater than that of the first pulse, the second pulse has the same sign as the first, otherwise the opposite.
- Thus, seven bits per track are transmitted to the receiver, plus five bits for the so-called "FCB amplification.
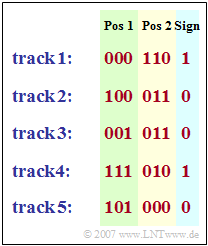
In the diagram, the $35$ bits describing an FCB pulse are given as an example:
⇒ Track 1 includes
- a positive pulse $({\rm sign} = 1)$ at position $\big [1$ (first possible position for track 1) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}0$ (bit specification for "000") $= 1\big]$,
- another positive pulse $($since $110 > 000)$ at position $\big [1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.02cm}\text{times}\hspace{0.2cm}6$ (bit specification for " 110") = $31\hspace{0.05cm}\big].$
Track 2 includes.
- a negative pulse (${\rm sign} = 0$) at position $\big [2$ (first possible position for track 2) $\hspace{0.02cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}4$ (bit specification for " 100") $=22\hspace{0.05cm}\big],$
- a positive pulse $($sign reversal due to $011 > 100)$ at position $\big [2 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}3$ (bit specification for " 011") $=17\hspace{0.05cm}\big].$
Hint:
- This exercise belongs to the chapter "Speech Coding".
- When entering the pulse positions $N_{1}$ denotes the first triple of bits and $N_{2}$ the second.
- For example, for track $2$ one would have to enter the values $N_{1}=-22$ and $N_{2}=+17$.
Questions
Solution
(1) With the data rate $R_{\rm C} = 12.2 \ \rm kbit/s$, exactly $\underline{244 \ \rm bits}$ results within $20 \ \rm ms$, while e.g. in $4.75 \ \rm kbit/s$ mode only $95 \ \rm bits$ are transmitted.
(2) In each subframe, the FCB pulse requires $35 \ \rm bits$ (five tracks of seven bits each) and the FCB gain requires five bits.
- With four subframes, this gives $N_{\rm FCB} \hspace{0.15cm}\underline{= 160 \ \rm bits}$.
(3) This leaves the difference from (1) and (2), i.e. $N_{\rm LPC/LTP}\hspace{0.15cm} \underline{ = 84\ \rm bits}$.
(4) The sign bit "$0$" indicates a negative first pulse.
- Because $001 < 011$, the second pulse has the same sign.
- The two magnitudes result in
- $$|N_1| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 1 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 001)} = 8\hspace{0.05cm}, $$
- $$ |N_2| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 3 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 011)} = 18\hspace{0.05cm}.$$
- Therefore, to be entered for the third track is $N_{1}\hspace{0.15cm} \underline{ = -8}$ and $N_{2} \hspace{0.15cm}\underline{ = -18}.$
(5) In an analogous way, for track $4$ we obtain the values $N_{1}\hspace{0.15cm} \underline{ = +39}$ and $N_{2}\hspace{0.15cm} \underline{ = -14}$.
(6) The fifth track provides $N_{1}\hspace{0.15cm} \underline{ =-30}$ and $N_{2}\hspace{0.15cm} \underline{ = +5}$