Difference between revisions of "Aufgaben:Exercise 3.7: Comparison of Two Convolutional Encoders"
From LNTwww
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Code_Description_with_State_and_Trellis_Diagram}} |
| − | [[File: | + | [[File:EN_KC_A_3_7_neu_v2.png|right|frame|Two convolutional encoders with parameters $n = 2, \ k = 1, \ m = 2$]] |
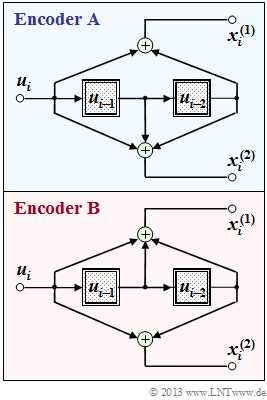
| − | + | The graph shows two rate $1/2$ convolutional encoders, each with memory $m = 2$: | |
| − | * | + | * The encoder $\rm A$ has the transfer function matrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$. |
| − | |||
| + | * In encoder $\rm B$ the two filters $($top and bottom$)$ are interchanged, and it holds: | ||
| + | :$$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$ | ||
| − | |||
| + | The lower encoder $\rm B$ has already been treated in detail in the theory part. | ||
| + | In the present exercise, | ||
| + | *you are first to determine the state transition diagram for encoder $\rm A$, | ||
| + | *and then work out the differences and the similarities between the two state diagrams. | ||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram| "Code description with state and trellis diagram"]]. | ||
| + | |||
| + | *Reference is made in particular to the sections | ||
| + | :* [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#State_definition_for_a_memory_register|"State definition for a memory register"]] and. | ||
| + | :* [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Representation_in_the_state_transition_diagram|"Representation in the state transition diagram"]]. | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { $\underline{u} = (0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$ holds. Which sequences does encoder $\rm A$ generate? |
|type="[]"} | |type="[]"} | ||
| − | + $\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$, | + | + $\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$, |
| − | - $\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, ...)$, | + | - $\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$, |
| − | - $\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$, | + | - $\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$, |
| − | + $\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, ...)$. | + | + $\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$. |
| − | { | + | {Which of the above state transitions exist in encoder $\rm A$? |
|type="[]"} | |type="[]"} | ||
+ $s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$. | + $s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$. | ||
| Line 32: | Line 44: | ||
+ $s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$. | + $s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$. | ||
| − | { | + | {How do the two state transition diagrams differ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Other state transitions are possible. |
| − | - | + | - All eight transitions have different code sequences. |
| − | + | + | + Differences exist only for the code sequences "$(01)$" and "$(10)$". |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | [[File:P_ID2673__KC_A_3_7a_neu.png|right|frame|Calculation of the code sequence]] | |
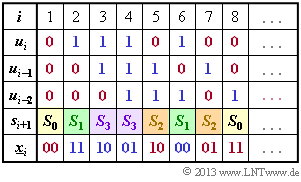
| − | + | '''(1)''' The calculation is based on the equations | |
| − | + | :$$x_i^{(1)} = u_i + u_{i–2},$$ | |
| − | + | :$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$ | |
| − | + | *Initially, the two memories $(u_{i–1}$ and $u_{i–2})$ are preallocated with zeros ⇒ $s_1 = S_0$. | |
| − | + | ||
| + | *With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$. | ||
| − | + | *With $u_2 = 1$, one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$. | |
| − | + | From the adjacent calculation scheme one recognizes the correctness of the <u>proposed solutions 1 and 4</u>. | |
| − | |||
| + | [[File:P_ID2674__KC_A_3_7b.png|right|frame|State transition diagram of encoder $\rm A$]] | ||
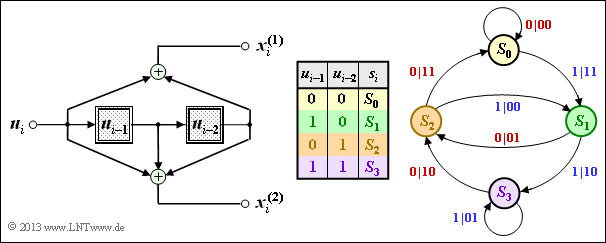
| + | '''(2)''' <u>All proposed solutions</u> are correct: | ||
| + | *This can be seen by evaluating the table at subtask '''(1)'''. | ||
| + | |||
| + | *The results are shown in the adjacent graph. | ||
| + | <br clear=all> | ||
| + | [[File:P_ID2675__KC_A_3_7c.png|right|frame|State transition diagram of encoder $\rm B$]] | ||
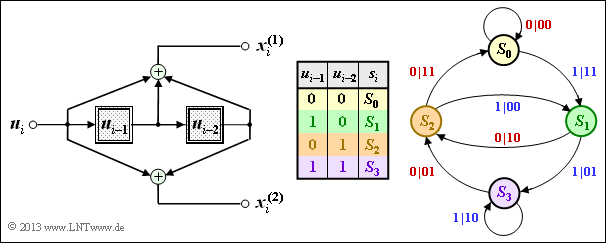
| + | '''(3)''' Correct is only <u>statement 3</u>: | ||
| + | *The state transition diagram of encoder $\rm B$ is sketched on the right. For derivation and interpretation, see section [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Representation_in_the_state_transition_diagram|"Representation in the state transition diagram"]]. | ||
| − | + | *If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder $\rm A$ to the convolutional encoder $\rm B$ $($and vice versa$)$. | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^3.3 State and Trellis Diagram^]] |
Latest revision as of 18:09, 16 November 2022
The graph shows two rate $1/2$ convolutional encoders, each with memory $m = 2$:
- The encoder $\rm A$ has the transfer function matrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$.
- In encoder $\rm B$ the two filters $($top and bottom$)$ are interchanged, and it holds:
- $$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$
The lower encoder $\rm B$ has already been treated in detail in the theory part.
In the present exercise,
- you are first to determine the state transition diagram for encoder $\rm A$,
- and then work out the differences and the similarities between the two state diagrams.
Hints:
- This exercise belongs to the chapter "Code description with state and trellis diagram".
- Reference is made in particular to the sections
Questions
Solution
(1) The calculation is based on the equations
- $$x_i^{(1)} = u_i + u_{i–2},$$
- $$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$
- Initially, the two memories $(u_{i–1}$ and $u_{i–2})$ are preallocated with zeros ⇒ $s_1 = S_0$.
- With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$.
- With $u_2 = 1$, one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$.
From the adjacent calculation scheme one recognizes the correctness of the proposed solutions 1 and 4.
(2) All proposed solutions are correct:
- This can be seen by evaluating the table at subtask (1).
- The results are shown in the adjacent graph.
(3) Correct is only statement 3:
- The state transition diagram of encoder $\rm B$ is sketched on the right. For derivation and interpretation, see section "Representation in the state transition diagram".
- If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder $\rm A$ to the convolutional encoder $\rm B$ $($and vice versa$)$.