Difference between revisions of "Aufgaben:Exercise 4.6Z: ISDN Supply Lines"
From LNTwww
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Properties_of_Balanced_Copper_Pairs |
}} | }} | ||
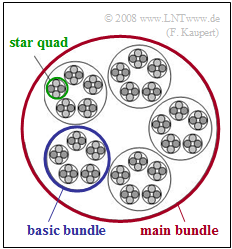
| − | [[File: | + | [[File:EN_Bei_A_1_1.png|right|frame|Main bundle, basic bundle and star quad]] |
| − | + | In [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_ISDN|$\rm ISDN$]] ("Integrated Services Digital Networks"), the terminal (near the subscriber) is connected to a local exchange ("OVSt") by a copper pair, with two pairs twisted into a so-called "star quad". | |
| + | *Several such star quad pairs are twisted to form a basic bundle, | ||
| + | *several basic bundles are combined to form a main bundle (see diagram). | ||
| − | + | ||
| + | In the network of Deutschen Telekom (formerly: Deutsche Bundespost), mostly copper lines with $\text{0.4 mm}$ core diameter are found, for whose attenuation and phase function given in [PW95] are the following equations: | ||
:$${{a}_{\rm K}(f)}/{\rm dB} = \left [ 5.1 + 14.3 \cdot \left ({f}/{\rm MHz}\right )^{0.59}\right ]\cdot{l}/{\rm km} | :$${{a}_{\rm K}(f)}/{\rm dB} = \left [ 5.1 + 14.3 \cdot \left ({f}/{\rm MHz}\right )^{0.59}\right ]\cdot{l}/{\rm km} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
:$${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} | :$${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Here $l$ denotes the line length. | |
| Line 17: | Line 20: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Eigenschaften_von_Kupfer–Doppeladern|Properties of Balanced Copper Pairs]]. | ||
| + | *For more information on the attenuation behavior of copper lines, see the page [[Examples_of_Communication_Systems/General_Description_of_ISDN#Four-wire_and_two-wire_transmission|Four-wire and two-wire transmission]] in the book "Examples of Communication Systems". | ||
| + | |||
| + | *You can use the interactive HTML5/JS applet [[Applets:Attenuation_of_Copper_Cables|"Attenuation of copper cables"]] to check your results. | ||
| + | *[PW95] denotes the following literature reference: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995. | ||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many subscribers $(N)$ can be connected to an ISDN local exchange via the main cable shown at the beginning? |
|type="{}"} | |type="{}"} | ||
$N \ = \ $ { 50 3% } | $N \ = \ $ { 50 3% } | ||
| − | { | + | {What are the consequences of two-wire transmission? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The two transmission directions can interfere with each other. |
| − | + | + | + Crosstalk interference can occur. |
| − | - | + | - Intersymbol interference occurs. |
| − | { | + | {A DC signal is attenuated by a factor of $4$. What is the cable length $l$? |
|type="{}"} | |type="{}"} | ||
$l \ = \ $ { 2.36 3% } $\ \rm km$ | $l \ = \ $ { 2.36 3% } $\ \rm km$ | ||
| − | { | + | {What is the attenuation and phase for the frequency $f = 120 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$a_{\rm K}(f = 120\ \rm kHz)\ = \ $ { 21.7 3% } $\ \rm dB$ | $a_{\rm K}(f = 120\ \rm kHz)\ = \ $ { 21.7 3% } $\ \rm dB$ | ||
| Line 57: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Two-wire transmission is used in the connection area. The possible connections are therefore equal to the number of pairs in the main cable: |
| + | :$$N = 5 \cdot 5 \cdot 2 \hspace{0.15cm}\underline{= 50}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' <u>Solutions 1 and 2</u> are correct: | ||
| + | *In two-wire transmission, a direction separation method is required, namely the so-called "hybrid coil". This has the task that at receiver $\rm A$ only arrives the transmitted signal of subscriber $\rm B$, but not the own transmitted signal. This is generally quite successful with narrow-band signals – for example speech – but not completely ⇒ solution 1 is correct. | ||
| + | *Solution 2 is also correct. Due to inductive and capacitive couplings, crosstalk can occur from the twin wire located in the same star quad, whereby near-end crosstalk (i.e. the interfering transmitter and the interfered receiver are located together) leads to greater impairments than far-end crosstalk. | ||
| + | *On the other hand, the last solution is not correct. Intersymbol interference ⇒ the mutual interfering influence of neighboring symbols can certainly occur, but it is not related to two-wire transmission. The reason for such intersymbol interference is rather linear distortion, caused by a non-ideal attenuation or phase response. | ||
| + | |||
| − | '''( | + | '''(3)''' The DC attenuation by a factor of $4$ can be expressed as follows: |
| − | + | :$$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$ | |
| − | + | *With the given coefficient $\alpha_0 =5.1 \ \rm dB/km$, this gives the line length $l = 12.04/5.1\; \underline{= 2.36 \ \rm km}$. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(4)''' Using the given equations and $l = 2.36 \ \rm km$, we obtain: |
| − | $$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm},$$ | + | :$$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm},$$ |
| − | $$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$ | + | :$$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^4.3 Balanced Copper Twisted Pair^]] |
Latest revision as of 16:49, 24 October 2022
In $\rm ISDN$ ("Integrated Services Digital Networks"), the terminal (near the subscriber) is connected to a local exchange ("OVSt") by a copper pair, with two pairs twisted into a so-called "star quad".
- Several such star quad pairs are twisted to form a basic bundle,
- several basic bundles are combined to form a main bundle (see diagram).
In the network of Deutschen Telekom (formerly: Deutsche Bundespost), mostly copper lines with $\text{0.4 mm}$ core diameter are found, for whose attenuation and phase function given in [PW95] are the following equations:
- $${{a}_{\rm K}(f)}/{\rm dB} = \left [ 5.1 + 14.3 \cdot \left ({f}/{\rm MHz}\right )^{0.59}\right ]\cdot{l}/{\rm km} \hspace{0.05cm},$$
- $${b_{\rm K}(f)}/{\rm rad} = \left [ 32.9 \cdot ({f}/{\rm MHz}) + 2.26 \cdot \left ({f}/{\rm MHz}\right )^{0.5}\right ]\cdot {l}/{\rm km} \hspace{0.05cm}.$$
Here $l$ denotes the line length.
Notes:
- The exercise belongs to the chapter Properties of Balanced Copper Pairs.
- For more information on the attenuation behavior of copper lines, see the page Four-wire and two-wire transmission in the book "Examples of Communication Systems".
- You can use the interactive HTML5/JS applet "Attenuation of copper cables" to check your results.
- [PW95] denotes the following literature reference: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.
Questions
Solution
(1) Two-wire transmission is used in the connection area. The possible connections are therefore equal to the number of pairs in the main cable:
- $$N = 5 \cdot 5 \cdot 2 \hspace{0.15cm}\underline{= 50}.$$
(2) Solutions 1 and 2 are correct:
- In two-wire transmission, a direction separation method is required, namely the so-called "hybrid coil". This has the task that at receiver $\rm A$ only arrives the transmitted signal of subscriber $\rm B$, but not the own transmitted signal. This is generally quite successful with narrow-band signals – for example speech – but not completely ⇒ solution 1 is correct.
- Solution 2 is also correct. Due to inductive and capacitive couplings, crosstalk can occur from the twin wire located in the same star quad, whereby near-end crosstalk (i.e. the interfering transmitter and the interfered receiver are located together) leads to greater impairments than far-end crosstalk.
- On the other hand, the last solution is not correct. Intersymbol interference ⇒ the mutual interfering influence of neighboring symbols can certainly occur, but it is not related to two-wire transmission. The reason for such intersymbol interference is rather linear distortion, caused by a non-ideal attenuation or phase response.
(3) The DC attenuation by a factor of $4$ can be expressed as follows:
- $$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$
- With the given coefficient $\alpha_0 =5.1 \ \rm dB/km$, this gives the line length $l = 12.04/5.1\; \underline{= 2.36 \ \rm km}$.
(4) Using the given equations and $l = 2.36 \ \rm km$, we obtain:
- $$a_{\rm K}(f = 120\,{\rm kHz}) = (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB}\hspace{0.15cm}\underline{ \approx 21.7\,{\rm dB}}\hspace{0.05cm},$$
- $$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$