Difference between revisions of "Channel Coding/Examples of Binary Block Codes"
| (46 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Binary Block Codes for Channel Coding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Channel Models and Decision Structures |
| − | |Nächste Seite= | + | |Nächste Seite=General Description of Linear Block Codes |
}} | }} | ||
| − | == Single | + | == Single Parity-check Codes== |
<br> | <br> | ||
| − | + | The »'''Single parity-check code'''« $\rm (SPC)$ adds to the information block $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ a parity bit $p$: | |
| + | [[File:P ID2346 KC T 1 3 S1 v2.png|right|frame|Various single parity-check codes $(n = k + 1)$|class=fit]] | ||
| + | :$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} | ||
| + | \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | The graphic shows three coding examples: | ||
| + | *$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \hspace{0.15cm} (k = 2)$, | ||
| + | |||
| + | *$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \hspace{0.15cm} (k = 3)$, | ||
| + | |||
| + | *$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \hspace{0.15cm} (k = 4)$. | ||
| − | |||
| − | |||
| − | |||
| − | + | This very simple code can be characterized as follows: | |
| − | + | *From $n = k + 1$ follows for the »'''code rate'''« $R = k/n = (n-1)/n$ and for the »'''redundancy'''« $1-R = 1/n$. For $k = 2$, for example, the code rate is $2/3$ and the relative redundancy is $33.3\%$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | *The parity bit is obtained by »'''modulo–2'''« addition. This is the addition in the [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois field|$\text{Galois field}$]] to the base $2$ ⇒ $\rm GF(2)$, so that $1 \oplus 1 = 0$ results: |
::<math>p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k | ::<math>p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Thus every valid code word $\underline{x}$ contains an even number of ones. Expressed as $\oplus$ or in simplified notation according to the second equation, this condition reads: |
::<math> x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 | ::<math> x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 | ||
| − | \hspace{0.05cm}, \hspace{0.5cm}{\rm | + | \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} |
\sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} | \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} | ||
| − | , \hspace{0.3cm} {\rm | + | , \hspace{0.3cm} {\rm addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} |
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | + | *For $k = 2$ ⇒ $n = 3$ the following four code words result, where the parity bit $p$ is marked by a small arrow in each case: | |
| − | * | ||
::<math>\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} | ::<math>\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} | ||
\underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.</math> | \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.</math> | ||
| − | + | *This code $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$ is »'''linear'''« since the sum of any two code words again gives a valid code word, for example: | |
| − | * | ||
:$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$ | :$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$ | ||
| + | *For any $k$ ⇒ $n = k+1$ each code word differs from all others at an even number of positions. Thus, the minimum distance of the code is | ||
| + | :$$d_{\rm min} = 2.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Each $\text{single parity-check code (SPC)}$ can be formally described as follows: | ||
| − | {{ | + | ::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.</math> |
| − | |||
| − | + | *With the general code name $(n, \ k, \ d_{\rm min})$ any single parity–check code can also be named $\text{SPC }(n, \ n-1, \ 2)$ . | |
| − | * | + | *The top graph thus shows the $\text{SPC (3, 2, 2)}$, the $\text{SPC (4, 3, 2)}$, and the $\text{SPC (5, 4, 2)}$.}}<br> |
| − | |||
| − | + | The digital channel may change the code word $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ to the received word $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ holds: | |
:$$\underline{y}= \underline{x} \oplus \underline{e}.$$ | :$$\underline{y}= \underline{x} \oplus \underline{e}.$$ | ||
| − | + | For $\text{decoding the single parity-check code}$ one forms the so-called »'''syndrome'''«: | |
::<math>s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} | ::<math>s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | The result $s=1$ then indicates (at least) one bit error within the code word, while $s=0$ should be interpreted as follows: | ||
| + | *The transmission was error-free, or:<br> | ||
| + | *the number of bit errors is even.<br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We consider the $\text{SPC (4, 3, 2)}$ and assume that the all-zero word was sent. The table shows all possibilities that $f$ bits are falsified and gives the respective syndrome $s \in \{0, 1\}$. |
| − | + | [[File:P ID2382 KC T 1 3 S1c.png|right|frame|Possible received values at the $\text{SPC (4, 3, 2)}$ |class=fit]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | For the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC model}$]] with the crossover probability $\varepsilon = 1\%$ the following probabilities then result: | ||
| + | *The information word is correctly decoded (blue background): | ||
::<math>{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.</math> | ::<math>{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.</math> | ||
| − | * | + | *The decoder detects that transmission errors have occurred (green background): |
| − | : | + | :$${\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm odd} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f}$$ |
| + | :$$\Rightarrow \hspace{0.3cm} {\rm Pr}(s=1) \hspace{-0.1cm} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.$$ | ||
| − | * | + | *The information word is decoded incorrectly (red background): |
::<math>{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.</math> | ::<math>{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.</math> | ||
| − | + | We refer here to the HTML5/JavaScript applet [[Applets:Binomial_and_Poisson_Distribution_(Applet)|$\text{Binomial and Poisson Distribution}$]]. The results obtained here are also discussed in [[Aufgaben:Exercise_1.5:_SPC_(5,_4)_and_BEC_Model|$\text{Exercise 1.5}$]]. }}<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ Error correction of the single parity–check code is not possible for the BSC model unlike the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|$\text{BEC model}$]] ("Binary Erasure Channel"). |
| + | |||
| + | Bit errors are excluded with this one. If only one bit is erased $($"erasure", $\rm E)$, then due to the fact "the number of ones in the code word is even", error correction is also possible, for example for the $\text{SPC (5, 4, 2)}$: | ||
:<math>\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) | :<math>\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) | ||
| Line 102: | Line 103: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ Also with the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\text{AWGN model}$]] error correction is possible when applying "soft decision". For the following we assume bipolar signaling: |
| − | [[File:P ID2387 KC T 1 3 S1d v2.png|right|frame| | + | [[File:P ID2387 KC T 1 3 S1d v2.png|right|frame|To clarify "soft decision" at AWGN|class=fit]] |
| − | *$x=0$ ⇒   | + | *$x=0$ ⇒ $\tilde{x}= +1$, as well as |
| − | *$x=1$ ⇒   | + | *$x=1$ ⇒ $\tilde{x}= -1$.<br> |
| − | + | The graphic illustrates the facts presented here: | |
| − | * | + | *For example, the received vector is (red dots): |
::<math>\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.</math> | ::<math>\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.</math> | ||
| − | * | + | *With a hard decision $($threshold $G = 0$, only the signs are evaluated$)$ one would arrive at the following binary result $($green squares $Y_i = y_i/ \vert y_i \vert)$: |
::<math>\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.</math> | ::<math>\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.</math> | ||
| − | |||
| − | |||
| − | * | + | *In symbol notation, this gives $(0, 1, 1, 0, 1)$, which is not a valid code word of $\text{SPC (5, 4, 2)}$ ⇒ syndrome $s = 1$. So one, three or five bits must have been falsified.<br> |
| + | |||
| + | *The probability for three or five bit errors, however, is orders of magnitude smaller than that for a single error. The assumption of "one bit error" is therefore not unreasonable.<br> | ||
| − | * | + | *Since the received value $y_3$ is very close to the threshold $G = 0$ it is assumed that exactly this bit has been falsified. Thus, with "soft decision", the decision is for $\underline{z} = (0, 1, 0, 0, 1)$ ⇒ $\underline{v} = (0, 1, 0, 0)$. The block error probability ${\rm Pr}(\underline{v} \ne \underline{u})$ is thus lowest.}}<br><br> |
| − | |||
| − | |||
| − | |||
| − | == | + | == Repetition Codes== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A $\text{repetition code}$ ($\rm RC)$ is a linear binary $(n, \, k)$ block code of the form |
| − | ::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n): x_i = x_j \hspace{0. | + | ::<math>\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.25cm}{\rm for \hspace{0.25cm}all\hspace{0.35cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.</math> |
| − | * | + | *The code parameter $n$ denotes the code length. Independent of $n$ always holds $k = 1$. |
| − | * | + | |
| + | *Accordingly, there exist only the two code words $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$ and $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, which differ in $n$ binary places. | ||
| + | |||
| + | *From this follows for the minimum distance $d_{\rm min} = n$.}}<br> | ||
| − | [[File:P ID2347 KC T 1 3 S2 v2.png|right|frame| | + | The graphic shows repetition codes for $n=3$, $n=4$ and $n=5$. Such a repetition code has the following properties: |
| − | + | [[File:P ID2347 KC T 1 3 S2 v2.png|right|frame|Various repetition codes|class=fit]] | |
| − | + | ||
| − | * | + | *This $(n, \, 1, \, n)$ block code has the very small code rate $R = 1/n$. |
| − | * | + | |
| + | *So, such a code is only suitable for transferring or storing small files. | ||
| + | |||
| + | *On the other hand, the repetition code is very robust. | ||
| + | |||
| + | *In particular, in the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|$\text{BEC channel}$]] ("Binary Erasure Channel"), a single correctly transmitted bit at any position (all other bits may be erased) is sufficient to correctly decode the information word.<br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4: Decoding and error probabilities of the repetition code at the BSC channel}$ |
<br> | <br> | ||
| − | + | ||
| − | * | + | The [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC channel}$]] with $\varepsilon = 10\%$ applies. The decoding is based on the majority principle. |
| + | *For odd $n$ ⇒ $e=n-1$ bit errors can be detected and $t=(n-1)/2$ bit errors can be corrected. | ||
| + | |||
| + | *This gives for the probability of correct decoding of the information bit $u$: | ||
::<math>{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.</math> | ::<math>{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.</math> | ||
| − | * | + | *The following numerical values are valid for $n = 5$. That means: There are $t = 2$ bit errors correctable: |
::<math>{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%</math> | ::<math>{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%</math> | ||
::<math>\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.</math> | ::<math>\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.</math> | ||
| − | * | + | *On the other hand, with even $n$ only $t=n/2-1$ errors can be corrected. If $n$ is increased from $5$ to $6$, then only two bit errors within a code word can be corrected. A third bit error cannot be corrected, but at least it can be recognized: |
| − | ::<math>{\rm Pr}({\rm | + | ::<math>{\rm Pr}({\rm not\hspace{0.15cm} correctable\hspace{0.15cm} error}) |
= {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx | = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx | ||
1.46\,\%\hspace{0.05cm}. </math> | 1.46\,\%\hspace{0.05cm}. </math> | ||
| − | * | + | *An (undetected) decoding error $(v \ne u)$ results only when four or more bits have been falsified within the six bit word. As an approximation, assuming that five or six bit errors are much less likely than four: |
::<math>{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= | ::<math>{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= | ||
0.122\,\%\hspace{0.05cm}.</math> | 0.122\,\%\hspace{0.05cm}.</math> | ||
| − | * | + | *It is interesting to note that for $\text{RC(6, 1, 6)}$ the probability ${\rm Pr}(v = u)$ for a possible and correct decoding with $98.42\%$ is smaller than for $\text{RC (5, 1, 5)}$. <br>For the latter: ${\rm Pr}(v = u) \approx 99.15\%.$}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5: Performance of the repetition code at the AWGN channel}$ |
<br> | <br> | ||
| − | |||
| − | + | We now consider the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\text{AWGN channel}$]]. For uncoded transmission $($or the repetition code with $n=1)$ the received value is $y = \tilde{x}+\eta$ , where $\tilde{x} \in \{+1, -1\}$ denotes the information bit in bipolar signaling and $\eta$ denotes the noise term. To avoid confusion with the code parameter $n$ we have renamed the noise: $n → \eta$.<br> | |
| + | |||
| + | For the error probability, with the [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|$\text{complementary Gaussian error integral}$]] ${\rm Q}(x)$ | ||
::<math>{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) | ::<math>{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | + | where the following physical quantities are to be used: | |
| − | * | + | *the signal-to-noise ratio $\rm (SNR)$ $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,<br> |
| − | * | + | *the energy $E_{\rm S}$ per code symbol ⇒ "symbol energy",<br> |
| − | * | + | *the normalized standard deviation $\sigma$ of the noise, valid for the bipolar information bit $\tilde{x} \in \{+1, -1\}$, and<br> |
| − | * | + | *the constant (one-sided) noise power density $N_0$ of the AWGN noise.<br><br> |
| − | |||
| − | |||
| + | [[File:EN_KC_T_1_3_S2b.png|right|frame|Error probability of the repetition code at the AWGN channel|class=fit]] | ||
| + | In contrast, for a $(n,\ 1,\ n)$ repetition code, the input value of the maximum likelihood decoder $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$ with the following properties: | ||
::<math>\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} | ::<math>\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} | ||
| − | n{\rm - | + | n{\rm -fold \hspace{0.15cm}amplitude}</math> |
| − | \hspace{ | + | ::<math>\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fold \hspace{0.15cm}power}\hspace{0.05cm},</math> |
::<math>\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} | ::<math>\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} | ||
| − | n{\rm - | + | n{\rm -fold \hspace{0.15cm}variance:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},</math> |
::<math>\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho | ::<math>\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho | ||
\hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.</math> | \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.</math> | ||
| − | + | The error probability in double logarithmic representation is shown in the left graph. | |
| + | #As abscissa is $10 \cdot \lg \, (E_{\rm S}/N_0)$ plotted. | ||
| + | #The energy per bit $(E_{\rm B})$ is $n$ times larger than the symbol energy $E_{\rm S}$, as illustrated in the graph for $n=3$ . | ||
| + | <br clear=all> | ||
| + | This set of curves can be interpreted as follows: | ||
| + | *If one plots the error probability over the abscissa $10 \cdot \lg \, (E_{\rm S}/N_0)$ then $n$–times repetition over uncoded transmission $(n=1)$ results in a significant improvement.<br> | ||
| − | + | *The curve for the repetition factor $n$ is obtained by left shifting by $10 \cdot \lg \, n$ $($in $\rm dB)$ with respect to the comparison curve. <br>The gain is $4.77 \ {\rm dB} \ (n = 3)$ or $\approx 5 \ {\rm dB} \ (n = 5)$.<br> | |
| − | |||
| − | * | + | *However, a comparison at constant $E_{\rm S}$ is not fair, since with the repetition code $\text{RC (5, 1, 5)}$ one spends a factor $n$ larger energy for the transmission of an information bit than with uncoded transmission: $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$ |
| − | |||
| − | + | From the graph on the right, we can see that all the curves lie exactly on top of each other when plotted on the abscissa $10 \cdot \lg \, (E_{\rm B}/N_0)$.}}<br> | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion regarding repetition codes on the AWGN channel:}$ |
| − | * | + | *The error probability is independent of the repetition factor $n$ for a fair comparison: ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) |
\hspace{0.05cm}.$ | \hspace{0.05cm}.$ | ||
| − | * | + | *For the AWGN channel, no [[Channel_Coding/Decoding_of_Linear_Block_Codes#Coding_gain_-_bit_error_rate_with_AWGN|$\text{coding gain}$]] can be achieved by a repetition code.}}<br> |
| − | == | + | == Hamming Codes == |
<br> | <br> | ||
| − | [https:// | + | In 1962 [https://en.wikipedia.org/wiki/Richard_Hamming $\text{Richard Wesley Hamming}$] specified a class of binary block codes that differ in the number $m = 2, 3, \text{...} $ of added "parity bits". For this code class: |
| − | * | + | *The code length always results in $n = 2^m -1$. Consequently, only the lengths $n = 3$, $n = 7$, $n = 15$, $n = 31$, $n = 63$, $n = 127$, $n = 255$, etc. are possible.<br> |
| − | * | + | *An information word consists of $k = n-m$ bits. The code rate is therefore equal to |
::<math>R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, | ::<math>R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, | ||
| Line 228: | Line 240: | ||
\}\hspace{0.05cm}.</math> | \}\hspace{0.05cm}.</math> | ||
| − | * | + | *All Hamming codes have the minimum distance $d_{\rm min} = 3$. With larger code length $n$ one reaches $d_{\rm min} = 3$ already with less redundancy, i.e. with larger code rate $R$.<br> |
| − | * | + | *It further follows from the statement $d_{\rm min} = 3$ that here only $e = d_{\rm min} -1 =2$ errors can be detected and only one error can $t = (d_{\rm min} -1)/2 = 1$ correct errors.<br> |
| − | * | + | *The Hamming code $\text{HC (3, 1, 3)}$ is identical to the repetition code $\text{RP (3, 1, 3)}$ and is: |
| − | ::<math>\mathcal{C} = \{ (0, 0, 0) \hspace{0. | + | ::<math>\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.25cm}, (1, 1, 1) \big \}\hspace{0.05cm}. </math> |
| − | * | + | *In systematic coding, the first $k$ digits of each Hamming code word $\underline{x}$ are identical to the information word $\underline{u}$. This is then followed by $m = n-k$ parity bits: |
| − | ::<math>\underline{x} = ( x_1, x_2, ... \hspace{0.05cm}, x_n) = ( u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, p_2, ... \hspace{0.05cm}, p_{n-k}) | + | ::<math>\underline{x} = ( x_1,\ x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm},\ x_n) = ( u_1,\ u_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k,\ p_1,\ p_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ p_{n-k}) |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6: Parity equations of the (7, 4, 3) Hamming code}$ |
| − | + | [[File:P ID2353 KC T 1 3 S3 v2.png|right|frame|Chart of the $\text{HC (7, 4, 3)}$]] | |
| − | |||
| − | |||
| − | |||
| − | + | The $\text{(7, 4, 3)}$ Hamming code is illustrated by the diagram shown. From it one can derive the three conditions: | |
| − | |||
| + | ::<math>x_1 \oplus x_2 \oplus x_3 \oplus x_5 = 0 \hspace{0.05cm},</math> | ||
| + | ::<math>x_2 \oplus x_3 \oplus x_4 \oplus x_6 = 0 \hspace{0.05cm},</math> | ||
| + | ::<math>x_1 \oplus x_2 \oplus x_4 \oplus x_7 = 0 \hspace{0.05cm}. </math> | ||
| − | + | *In the diagram, the red circle indicates the first test equation, the green the second and the blue the last. | |
| + | |||
| + | *In each circle, the number of ones must be even. | ||
| − | :<math>x_1 = u_1 ,\hspace{0.2cm} | + | |
| + | [[File:P ID2351 KC T 1 3 S3c v2.png|right|frame|Assignment $\underline{u} → \underline{x}$ of the systematic $\text{(7, 4, 3)}$ Hamming code|class=fit]] | ||
| + | In systematic coding of the $\text{(7, 4, 3)}$ Hamming code | ||
| + | |||
| + | ::<math>x_1 = u_1 ,\hspace{0.2cm} | ||
x_2 = u_2 ,\hspace{0.2cm} | x_2 = u_2 ,\hspace{0.2cm} | ||
x_3 = u_3 ,\hspace{0.2cm} | x_3 = u_3 ,\hspace{0.2cm} | ||
| Line 263: | Line 279: | ||
x_7 = p_3 </math> | x_7 = p_3 </math> | ||
| − | + | are the equations of determination of the three test bits, as shown in the diagram: | |
| − | |||
| − | :<math>p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},</math> | + | ::<math>p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},</math> |
| − | :<math>p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},</math> | + | ::<math>p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},</math> |
| − | :<math>p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.</math> | + | ::<math>p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.</math> |
| − | + | ||
| − | + | The table shows the $2^k = 16$ allowed code words of the systematic $\text{HC (7, 4, 3)}$: | |
| − | + | :$$\underline{x} = ( x_1,\ x_2,\ x_3,\ x_4,\ x_5,\ x_6,\ x_7) = ( u_1,\ u_2,\ u_3,\ u_4,\ p_1,\ p_2,\ p_3).$$ | |
| − | * | + | *The information word $\underline{u} =( u_1,\ u_2,\ u_3,\ u_4)$ is shown in black and the check bits $p_1$, $p_2$ and $p_3$ in red. |
| + | |||
| + | *It can be seen from this table that each two of the $16$ possible code words differ in at least $d_{\rm min} = 3$ binary values.}}<br> | ||
| − | + | Later the [[Channel_Coding/Decoding_of_Linear_Block_Codes|$\text{Decoding of linear block codes}$]] will be covered in more detail. The following example is intended to explain the decoding of the Hamming code rather intuitively.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 7: Parity equations of the HC (7, 4, 3)}$ |
| − | <br> | + | <br> |
| + | |||
| + | We further assume the systematic $\text{(7, 4, 3)}$ Hamming code and consider the received word $\underline{y} = ( y_1,\ y_2,\ y_3,\ y_4,\ y_5,\ y_6,\ y_7)$. | ||
| + | |||
| + | For decoding, we form the three parity equations | ||
::<math> y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} </math> | ::<math> y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} </math> | ||
| Line 284: | Line 305: | ||
::<math>y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}</math> | ::<math>y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}</math> | ||
| − | + | In the following $\underline{v}$ denotes the decoding result; this should always match $\underline{u} = (1,\ 0,\ 1,\ 0)$. | |
| − | * | + | |
| + | Provided that at most one bit is falsified in each code word, the following statements are then valid: | ||
| + | *The received word $\underline{y} = (1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 1)$ satisfies all three parity equations. This means that not a single transmission error has occurred ⇒ $\underline{y} = \underline{x}$ ⇒ $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.<br> | ||
| − | * | + | *If two of the three parity equations are satisfied, such as for the received word $\underline{y} =(1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 0)$, then one parity bit has been falsified and the following also applies here $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.<br> |
| − | * | + | *With $\underline{y} = (1,\ 0,\ 1,\ 1,\ 0,\ 1,\ 1)$ only the equation $\rm (I)$ is satisfied and the other two are not. Thus, the falsification of the fourth binary symbol can be corrected, and it is also valid here $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.<br> |
| − | * | + | *A transmission error of the second bit ⇒ $\underline{y} = (1,\ 1,\ 1,\ 0,\ 0,\ 1,\ 1)$ leads to the fact that all three parity equations are not fulfilled. This error can also be clearly corrected since only $u_2$ occurs in all equations.}}<br> |
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5:_SPC_(5,_4)_and_BEC_Model|Exercise 1.5: SPC (5, 4) and BEC Model]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.5Z:_SPC_(5,_4)_vs._RC_(5,_1)|Exercise 1.5Z: SPC (5, 4) vs. RC (5, 1)]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.6:_(7,_4)_Hamming_Code|Exercise 1.6: (7, 4) Hamming Code]] |
{{Display}} | {{Display}} | ||
Latest revision as of 15:42, 23 January 2023
Single Parity-check Codes
The »Single parity-check code« $\rm (SPC)$ adds to the information block $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ a parity bit $p$:
- $$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$
- $$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$
The graphic shows three coding examples:
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \hspace{0.15cm} (k = 2)$,
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \hspace{0.15cm} (k = 3)$,
- $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \hspace{0.15cm} (k = 4)$.
This very simple code can be characterized as follows:
- From $n = k + 1$ follows for the »code rate« $R = k/n = (n-1)/n$ and for the »redundancy« $1-R = 1/n$. For $k = 2$, for example, the code rate is $2/3$ and the relative redundancy is $33.3\%$.
- The parity bit is obtained by »modulo–2« addition. This is the addition in the $\text{Galois field}$ to the base $2$ ⇒ $\rm GF(2)$, so that $1 \oplus 1 = 0$ results:
- \[p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]
- Thus every valid code word $\underline{x}$ contains an even number of ones. Expressed as $\oplus$ or in simplified notation according to the second equation, this condition reads:
- \[ x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]
- For $k = 2$ ⇒ $n = 3$ the following four code words result, where the parity bit $p$ is marked by a small arrow in each case:
- \[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.\]
- This code $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$ is »linear« since the sum of any two code words again gives a valid code word, for example:
- $$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$
- For any $k$ ⇒ $n = k+1$ each code word differs from all others at an even number of positions. Thus, the minimum distance of the code is
- $$d_{\rm min} = 2.$$
$\text{Definition:}$ Each $\text{single parity-check code (SPC)}$ can be formally described as follows:
- \[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.\]
- With the general code name $(n, \ k, \ d_{\rm min})$ any single parity–check code can also be named $\text{SPC }(n, \ n-1, \ 2)$ .
- The top graph thus shows the $\text{SPC (3, 2, 2)}$, the $\text{SPC (4, 3, 2)}$, and the $\text{SPC (5, 4, 2)}$.
The digital channel may change the code word $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ to the received word $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ holds:
- $$\underline{y}= \underline{x} \oplus \underline{e}.$$
For $\text{decoding the single parity-check code}$ one forms the so-called »syndrome«:
- \[s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]
The result $s=1$ then indicates (at least) one bit error within the code word, while $s=0$ should be interpreted as follows:
- The transmission was error-free, or:
- the number of bit errors is even.
$\text{Example 1:}$ We consider the $\text{SPC (4, 3, 2)}$ and assume that the all-zero word was sent. The table shows all possibilities that $f$ bits are falsified and gives the respective syndrome $s \in \{0, 1\}$.
For the $\text{BSC model}$ with the crossover probability $\varepsilon = 1\%$ the following probabilities then result:
- The information word is correctly decoded (blue background):
- \[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]
- The decoder detects that transmission errors have occurred (green background):
- $${\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm odd} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f}$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}(s=1) \hspace{-0.1cm} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.$$
- The information word is decoded incorrectly (red background):
- \[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]
We refer here to the HTML5/JavaScript applet $\text{Binomial and Poisson Distribution}$. The results obtained here are also discussed in $\text{Exercise 1.5}$.
$\text{Example 2:}$ Error correction of the single parity–check code is not possible for the BSC model unlike the $\text{BEC model}$ ("Binary Erasure Channel").
Bit errors are excluded with this one. If only one bit is erased $($"erasure", $\rm E)$, then due to the fact "the number of ones in the code word is even", error correction is also possible, for example for the $\text{SPC (5, 4, 2)}$:
\[\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]
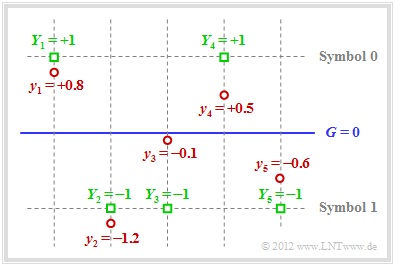
$\text{Example 3:}$ Also with the $\text{AWGN model}$ error correction is possible when applying "soft decision". For the following we assume bipolar signaling:
- $x=0$ ⇒ $\tilde{x}= +1$, as well as
- $x=1$ ⇒ $\tilde{x}= -1$.
The graphic illustrates the facts presented here:
- For example, the received vector is (red dots):
- \[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]
- With a hard decision $($threshold $G = 0$, only the signs are evaluated$)$ one would arrive at the following binary result $($green squares $Y_i = y_i/ \vert y_i \vert)$:
- \[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]
- In symbol notation, this gives $(0, 1, 1, 0, 1)$, which is not a valid code word of $\text{SPC (5, 4, 2)}$ ⇒ syndrome $s = 1$. So one, three or five bits must have been falsified.
- The probability for three or five bit errors, however, is orders of magnitude smaller than that for a single error. The assumption of "one bit error" is therefore not unreasonable.
- Since the received value $y_3$ is very close to the threshold $G = 0$ it is assumed that exactly this bit has been falsified. Thus, with "soft decision", the decision is for $\underline{z} = (0, 1, 0, 0, 1)$ ⇒ $\underline{v} = (0, 1, 0, 0)$. The block error probability ${\rm Pr}(\underline{v} \ne \underline{u})$ is thus lowest.
Repetition Codes
$\text{Definition:}$ A $\text{repetition code}$ ($\rm RC)$ is a linear binary $(n, \, k)$ block code of the form
- \[\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.25cm}{\rm for \hspace{0.25cm}all\hspace{0.35cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.\]
- The code parameter $n$ denotes the code length. Independent of $n$ always holds $k = 1$.
- Accordingly, there exist only the two code words $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$ and $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, which differ in $n$ binary places.
- From this follows for the minimum distance $d_{\rm min} = n$.
The graphic shows repetition codes for $n=3$, $n=4$ and $n=5$. Such a repetition code has the following properties:
- This $(n, \, 1, \, n)$ block code has the very small code rate $R = 1/n$.
- So, such a code is only suitable for transferring or storing small files.
- On the other hand, the repetition code is very robust.
- In particular, in the $\text{BEC channel}$ ("Binary Erasure Channel"), a single correctly transmitted bit at any position (all other bits may be erased) is sufficient to correctly decode the information word.
$\text{Example 4: Decoding and error probabilities of the repetition code at the BSC channel}$
The $\text{BSC channel}$ with $\varepsilon = 10\%$ applies. The decoding is based on the majority principle.
- For odd $n$ ⇒ $e=n-1$ bit errors can be detected and $t=(n-1)/2$ bit errors can be corrected.
- This gives for the probability of correct decoding of the information bit $u$:
- \[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]
- The following numerical values are valid for $n = 5$. That means: There are $t = 2$ bit errors correctable:
- \[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]
- \[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]
- On the other hand, with even $n$ only $t=n/2-1$ errors can be corrected. If $n$ is increased from $5$ to $6$, then only two bit errors within a code word can be corrected. A third bit error cannot be corrected, but at least it can be recognized:
- \[{\rm Pr}({\rm not\hspace{0.15cm} correctable\hspace{0.15cm} error}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]
- An (undetected) decoding error $(v \ne u)$ results only when four or more bits have been falsified within the six bit word. As an approximation, assuming that five or six bit errors are much less likely than four:
- \[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]
- It is interesting to note that for $\text{RC(6, 1, 6)}$ the probability ${\rm Pr}(v = u)$ for a possible and correct decoding with $98.42\%$ is smaller than for $\text{RC (5, 1, 5)}$.
For the latter: ${\rm Pr}(v = u) \approx 99.15\%.$
$\text{Example 5: Performance of the repetition code at the AWGN channel}$
We now consider the $\text{AWGN channel}$. For uncoded transmission $($or the repetition code with $n=1)$ the received value is $y = \tilde{x}+\eta$ , where $\tilde{x} \in \{+1, -1\}$ denotes the information bit in bipolar signaling and $\eta$ denotes the noise term. To avoid confusion with the code parameter $n$ we have renamed the noise: $n → \eta$.
For the error probability, with the $\text{complementary Gaussian error integral}$ ${\rm Q}(x)$
- \[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]
where the following physical quantities are to be used:
- the signal-to-noise ratio $\rm (SNR)$ $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,
- the energy $E_{\rm S}$ per code symbol ⇒ "symbol energy",
- the normalized standard deviation $\sigma$ of the noise, valid for the bipolar information bit $\tilde{x} \in \{+1, -1\}$, and
- the constant (one-sided) noise power density $N_0$ of the AWGN noise.
In contrast, for a $(n,\ 1,\ n)$ repetition code, the input value of the maximum likelihood decoder $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$ with the following properties:
- \[\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}amplitude}\]
- \[\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fold \hspace{0.15cm}power}\hspace{0.05cm},\]
- \[\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}variance:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\]
- \[\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.\]
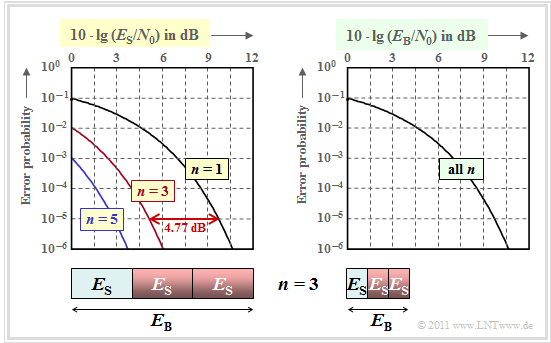
The error probability in double logarithmic representation is shown in the left graph.
- As abscissa is $10 \cdot \lg \, (E_{\rm S}/N_0)$ plotted.
- The energy per bit $(E_{\rm B})$ is $n$ times larger than the symbol energy $E_{\rm S}$, as illustrated in the graph for $n=3$ .
This set of curves can be interpreted as follows:
- If one plots the error probability over the abscissa $10 \cdot \lg \, (E_{\rm S}/N_0)$ then $n$–times repetition over uncoded transmission $(n=1)$ results in a significant improvement.
- The curve for the repetition factor $n$ is obtained by left shifting by $10 \cdot \lg \, n$ $($in $\rm dB)$ with respect to the comparison curve.
The gain is $4.77 \ {\rm dB} \ (n = 3)$ or $\approx 5 \ {\rm dB} \ (n = 5)$.
- However, a comparison at constant $E_{\rm S}$ is not fair, since with the repetition code $\text{RC (5, 1, 5)}$ one spends a factor $n$ larger energy for the transmission of an information bit than with uncoded transmission: $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$
From the graph on the right, we can see that all the curves lie exactly on top of each other when plotted on the abscissa $10 \cdot \lg \, (E_{\rm B}/N_0)$.
$\text{Conclusion regarding repetition codes on the AWGN channel:}$
- The error probability is independent of the repetition factor $n$ for a fair comparison: ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$
- For the AWGN channel, no $\text{coding gain}$ can be achieved by a repetition code.
Hamming Codes
In 1962 $\text{Richard Wesley Hamming}$ specified a class of binary block codes that differ in the number $m = 2, 3, \text{...} $ of added "parity bits". For this code class:
- The code length always results in $n = 2^m -1$. Consequently, only the lengths $n = 3$, $n = 7$, $n = 15$, $n = 31$, $n = 63$, $n = 127$, $n = 255$, etc. are possible.
- An information word consists of $k = n-m$ bits. The code rate is therefore equal to
- \[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.\]
- All Hamming codes have the minimum distance $d_{\rm min} = 3$. With larger code length $n$ one reaches $d_{\rm min} = 3$ already with less redundancy, i.e. with larger code rate $R$.
- It further follows from the statement $d_{\rm min} = 3$ that here only $e = d_{\rm min} -1 =2$ errors can be detected and only one error can $t = (d_{\rm min} -1)/2 = 1$ correct errors.
- The Hamming code $\text{HC (3, 1, 3)}$ is identical to the repetition code $\text{RP (3, 1, 3)}$ and is:
- \[\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.25cm}, (1, 1, 1) \big \}\hspace{0.05cm}. \]
- In systematic coding, the first $k$ digits of each Hamming code word $\underline{x}$ are identical to the information word $\underline{u}$. This is then followed by $m = n-k$ parity bits:
- \[\underline{x} = ( x_1,\ x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm},\ x_n) = ( u_1,\ u_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k,\ p_1,\ p_2,\ \hspace{0.05cm}\text{...} \hspace{0.05cm},\ p_{n-k}) \hspace{0.05cm}.\]
$\text{Example 6: Parity equations of the (7, 4, 3) Hamming code}$
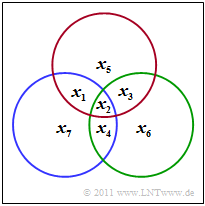
The $\text{(7, 4, 3)}$ Hamming code is illustrated by the diagram shown. From it one can derive the three conditions:
- \[x_1 \oplus x_2 \oplus x_3 \oplus x_5 = 0 \hspace{0.05cm},\]
- \[x_2 \oplus x_3 \oplus x_4 \oplus x_6 = 0 \hspace{0.05cm},\]
- \[x_1 \oplus x_2 \oplus x_4 \oplus x_7 = 0 \hspace{0.05cm}. \]
- In the diagram, the red circle indicates the first test equation, the green the second and the blue the last.
- In each circle, the number of ones must be even.
In systematic coding of the $\text{(7, 4, 3)}$ Hamming code
- \[x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3 \]
are the equations of determination of the three test bits, as shown in the diagram:
- \[p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},\]
- \[p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},\]
- \[p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.\]
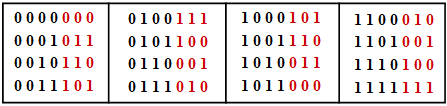
The table shows the $2^k = 16$ allowed code words of the systematic $\text{HC (7, 4, 3)}$:
- $$\underline{x} = ( x_1,\ x_2,\ x_3,\ x_4,\ x_5,\ x_6,\ x_7) = ( u_1,\ u_2,\ u_3,\ u_4,\ p_1,\ p_2,\ p_3).$$
- The information word $\underline{u} =( u_1,\ u_2,\ u_3,\ u_4)$ is shown in black and the check bits $p_1$, $p_2$ and $p_3$ in red.
- It can be seen from this table that each two of the $16$ possible code words differ in at least $d_{\rm min} = 3$ binary values.
Later the $\text{Decoding of linear block codes}$ will be covered in more detail. The following example is intended to explain the decoding of the Hamming code rather intuitively.
$\text{Example 7: Parity equations of the HC (7, 4, 3)}$
We further assume the systematic $\text{(7, 4, 3)}$ Hamming code and consider the received word $\underline{y} = ( y_1,\ y_2,\ y_3,\ y_4,\ y_5,\ y_6,\ y_7)$.
For decoding, we form the three parity equations
- \[ y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} \]
- \[y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)} \]
- \[y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}\]
In the following $\underline{v}$ denotes the decoding result; this should always match $\underline{u} = (1,\ 0,\ 1,\ 0)$.
Provided that at most one bit is falsified in each code word, the following statements are then valid:
- The received word $\underline{y} = (1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 1)$ satisfies all three parity equations. This means that not a single transmission error has occurred ⇒ $\underline{y} = \underline{x}$ ⇒ $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
- If two of the three parity equations are satisfied, such as for the received word $\underline{y} =(1,\ 0,\ 1,\ 0,\ 0,\ 1,\ 0)$, then one parity bit has been falsified and the following also applies here $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
- With $\underline{y} = (1,\ 0,\ 1,\ 1,\ 0,\ 1,\ 1)$ only the equation $\rm (I)$ is satisfied and the other two are not. Thus, the falsification of the fourth binary symbol can be corrected, and it is also valid here $\underline{v} = \underline{u} = (1,\ 0,\ 1,\ 0)$.
- A transmission error of the second bit ⇒ $\underline{y} = (1,\ 1,\ 1,\ 0,\ 0,\ 1,\ 1)$ leads to the fact that all three parity equations are not fulfilled. This error can also be clearly corrected since only $u_2$ occurs in all equations.
Exercises for the chapter
Exercise 1.5: SPC (5, 4) and BEC Model
Exercise 1.5Z: SPC (5, 4) vs. RC (5, 1)
Exercise 1.6: (7, 4) Hamming Code