Difference between revisions of "Aufgaben:Exercise 3.5: GSM Full Rate Vocoder"
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Voice_Coding |
}} | }} | ||
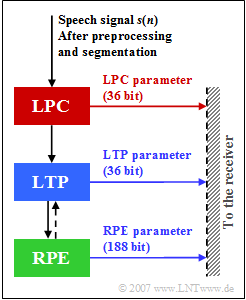
| − | [[File: | + | [[File:EN_Mob_A_3_4_Z.png|right|frame|LPC, LTP and RPE parameters in the GSM Full Rate Vocoder]] |
| − | + | This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of encoder and decoder and combines three methods for the compression of speech signals: | |
| − | *Linear Predictive Coding (LPC), | + | *Linear Predictive Coding $\rm (LPC)$, |
| − | |||
| − | |||
| + | *Long Term Prediction $\rm (LTP)$, and | ||
| − | + | *Regular Pulse Excitation $\rm (RPE)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The numbers shown in the graphic indicate the number of bits generated by the three units of this full rate speech codec per frame of $20$ millisecond duration each. | ||
| − | + | It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the exercise. | |
| + | The input signal in the above graphic is the digitalized speech signal $s_{\rm block}(n)$. This results from the analog speech signal $s(t)$ by | ||
| + | *a suitable limitation to the bandwidth $B$, | ||
| + | *sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$, | ||
| + | *quantization with $13 \ \rm bits$, | ||
| + | *following segmentation into blocks of each $20 \ \rm ms$. | ||
| + | The further tasks of preprocessing will not be discussed in detail here. | ||
| − | |||
| − | + | ||
| + | <u>Hint:</u> This exercise belongs to the chapter [[Examples_of_Communication_Systems/Voice_Coding|"Speech Coding"]]. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {To what bandwidth must the speech signal be limited? |
|type="{}"} | |type="{}"} | ||
$B \ = \ $ { 4 3% } $ \ \rm kHz$ | $B \ = \ $ { 4 3% } $ \ \rm kHz$ | ||
| − | { | + | {How many samples $(N_{\rm block})$ does a speech lock consist of? What is the input data rate $R_{\rm in}$? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm block} \hspace{0.25cm} = \ $ { 160 3% } |
| − | $R_{\rm | + | $R_{\rm in} \hspace{0.22cm} = \ $ { 104 3% } $\ \rm kbit/s$ |
| − | { | + | {What is the output data rate $R_{\rm out}$ of the GSM full rate codec? |
|type="{}"} | |type="{}"} | ||
| − | $R_{\rm | + | $R_{\rm out} \hspace{0.09cm} = \ $ { 13 3% } $ \ \rm kbit/s$ |
| − | { | + | {Which statements are true regarding the block "LPC"? |
|type="[]"} | |type="[]"} | ||
| − | + LPC | + | + LPC makes a short-term prediction over one millisecond. |
| − | + | + | + The $36$ LPC bits are filter coefficients used at the receiver to undo the LPC filtering. |
| − | - | + | - The filter for long-term prediction is recursive. |
| − | - | + | - The LPC output is identical to its input $s_{\rm block}(t)$. |
| − | { | + | {Which statements are true regarding the block "LTP"? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Periodic structures of the speech signal are removed. |
| − | - | + | - Long-term prediction is performed once per block. |
| − | + | + | + The memory of the LTP predictor is up to $15 \ \rm ms$. |
| − | { | + | {Which statements are true for the block "RPE"? |
|type="[]"} | |type="[]"} | ||
| − | - RPE | + | - RPE provides less information than LPC and LTP. |
| − | + RPE | + | + RPE removes parts that are unimportant for the subjective impression. |
| − | + RPE | + | + RPE divides each subblock again into four sub-sequences. |
| − | - RPE | + | - RPE selects the subsequence with the minimum energy. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' To satisfy the sampling theorem, the bandwidth must not exceed $f_{\rm A}/2 \hspace{0.15cm} \underline{= 4 \ \rm kHz}$. |
| + | |||
| + | |||
| + | '''(2)''' From the given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$. | ||
| + | *Thus, a speech block $(20 \ \rm ms)$ consists of $N_{\rm block} = 20/0.125\hspace{0.15cm} \underline{= 160 \ \rm samples}$, each quantized with $13 \ \rm bits$. | ||
| + | |||
| + | *The data rate is thus | ||
| + | :$$R_{\rm in} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' From the graph, it can be seen that $36$ (LPC) $+\ 36$ (LTP) $+\ 188$ (RPE) $= 260 \ \rm bits$ are output per speech block. | ||
| + | *From this, the output data rate is calculated to be | ||
| + | :$$R_{\rm out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *The compression factor achieved by the full rate speech codec is thus $104/13 = 8$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' Correct are the <u>statements 1 and 2</u>: | ||
| + | *The $36$ LPC bits describe a total of eight filter coefficients of a non-recursive filter, where eight ACF values are determined from the short-time analysis. | ||
| − | + | *These are converted into reflection coefficients $r_{k}$ according to the so-called "Schur recursion". | |
| − | * | + | |
| − | + | *From these, the eight LAR coefficients are calculated according to the function ${\rm ln}[(1 - r_{k})/(1 + r_{k})]$, quantized with a different number of bits and passed on to the receiver. | |
| − | |||
| + | *The LPC output signal has a significantly smaller amplitude compared to its input $s_{\rm block}(n)$, has a significantly reduced dynamic range and a flatter spectrum. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(5)''' Correct are the <u>statements 1 and 3</u>, but not the second: | ||
| + | *The LTP analysis and filtering is done in blocks every $5 \rm ms \ (40 \rm samples)$, i.e. four times per speech block. | ||
| + | |||
| + | *To do this, the cross-correlation function (CCF) is formed between the current and the three preceding sub-blocks. | ||
| + | |||
| + | *For each sub-block, an LTP delay and an LTP gain are determined that best fit the sub-block. | ||
| + | |||
| + | *A correction signal of the subsequent component "RPE" is also taken into account. | ||
| + | |||
| + | *In the case of long-term prediction, as with LPC, the output is redundancy-reduced compared to the input. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(6)''' Correct are the <u>statements 2 and 3</u>: | ||
| + | *That statement 1 is false can already be seen from the graph on the statements page, since $188$ of the $260$ output bits come from the RPE. | ||
| + | *To the last statement: The RPE searches for the sub-sequence with the maximum energy. | ||
| − | + | *This parameter "RPE pulses" alone occupies $188$ of the $260$ output bits. | |
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 118: | Line 131: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^3.3 Speech Coding^]] |
Latest revision as of 10:39, 25 January 2023
This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of encoder and decoder and combines three methods for the compression of speech signals:
- Linear Predictive Coding $\rm (LPC)$,
- Long Term Prediction $\rm (LTP)$, and
- Regular Pulse Excitation $\rm (RPE)$.
The numbers shown in the graphic indicate the number of bits generated by the three units of this full rate speech codec per frame of $20$ millisecond duration each.
It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the exercise.
The input signal in the above graphic is the digitalized speech signal $s_{\rm block}(n)$. This results from the analog speech signal $s(t)$ by
- a suitable limitation to the bandwidth $B$,
- sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$,
- quantization with $13 \ \rm bits$,
- following segmentation into blocks of each $20 \ \rm ms$.
The further tasks of preprocessing will not be discussed in detail here.
Hint: This exercise belongs to the chapter "Speech Coding".
Questions
Solution
(1) To satisfy the sampling theorem, the bandwidth must not exceed $f_{\rm A}/2 \hspace{0.15cm} \underline{= 4 \ \rm kHz}$.
(2) From the given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$.
- Thus, a speech block $(20 \ \rm ms)$ consists of $N_{\rm block} = 20/0.125\hspace{0.15cm} \underline{= 160 \ \rm samples}$, each quantized with $13 \ \rm bits$.
- The data rate is thus
- $$R_{\rm in} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$
(3) From the graph, it can be seen that $36$ (LPC) $+\ 36$ (LTP) $+\ 188$ (RPE) $= 260 \ \rm bits$ are output per speech block.
- From this, the output data rate is calculated to be
- $$R_{\rm out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$
- The compression factor achieved by the full rate speech codec is thus $104/13 = 8$.
(4) Correct are the statements 1 and 2:
- The $36$ LPC bits describe a total of eight filter coefficients of a non-recursive filter, where eight ACF values are determined from the short-time analysis.
- These are converted into reflection coefficients $r_{k}$ according to the so-called "Schur recursion".
- From these, the eight LAR coefficients are calculated according to the function ${\rm ln}[(1 - r_{k})/(1 + r_{k})]$, quantized with a different number of bits and passed on to the receiver.
- The LPC output signal has a significantly smaller amplitude compared to its input $s_{\rm block}(n)$, has a significantly reduced dynamic range and a flatter spectrum.
(5) Correct are the statements 1 and 3, but not the second:
- The LTP analysis and filtering is done in blocks every $5 \rm ms \ (40 \rm samples)$, i.e. four times per speech block.
- To do this, the cross-correlation function (CCF) is formed between the current and the three preceding sub-blocks.
- For each sub-block, an LTP delay and an LTP gain are determined that best fit the sub-block.
- A correction signal of the subsequent component "RPE" is also taken into account.
- In the case of long-term prediction, as with LPC, the output is redundancy-reduced compared to the input.
(6) Correct are the statements 2 and 3:
- That statement 1 is false can already be seen from the graph on the statements page, since $188$ of the $260$ output bits come from the RPE.
- To the last statement: The RPE searches for the sub-sequence with the maximum energy.
- This parameter "RPE pulses" alone occupies $188$ of the $260$ output bits.