Difference between revisions of "Aufgaben:Exercise 4.7: About the Rake Receiver"
m (Guenter moved page Exercise 4.7: To the Rake Receiver to Exercise 4.7: About the Rake Receiver) |
|||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS}} |
| − | [[File: | + | [[File:EN_Mod_Z_5_5.png|right|frame|Two-way channel <br>& rake receiver]] |
| − | + | The graphic shows a two-way channel (yellow background). The corresponding description equation is: | |
:$$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ | :$$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ | ||
| − | + | Let the delay on the side path be $\tau = 1 \ \rm µ s$. Drawn below is the structure of a RAKE receiver (green background) with general coefficients $K, \ h_{0}, \ h_{1}, \ \tau_{0}$ and $\tau_{1}$. | |
| − | + | The RAKE receiver has the task of combining the energy of the two signal paths to make the decision more reliable. The joint impulse response of the channel and the RAKE receiver can be expressed in the form | |
:$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ | :$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ | ||
| − | + | can be given, but only if the RAKE coefficients $h_{0}, \ h_{1}, \ \tau_{0}$ and $\tau_{1}$ are appropriately chosen. The main part of $h_{\rm KR}(t)$ shall be at $t = \tau$ . | |
| − | + | The constant $K$ is necessary for normalization reasons. In order not to distort the influence of AWGN noise, the following condition must be fulfilled: | |
:$$K= \frac{1}{h_0^2 + h_1^2}.$$ | :$$K= \frac{1}{h_0^2 + h_1^2}.$$ | ||
| − | + | Besides the appropriate RAKE parameters, the signals $r(t)$ and $b(t)$ are also sought if $s(t)$ describes a rectangle of height $1$ and width $T = 5 \ \rm µ s$ . | |
| Line 28: | Line 28: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS|"Telecommunications Aspects of UMTS"]]. |
| − | * | + | *Reference is also made to the page [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation#Examinations_of_the_rake_receiver|"Examinations of the rake receiver"]] in the book "Modulation Methods". |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements are valid for the channel impulse response $h_{\rm K}(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $h_{\rm K}(t)$ | + | + $h_{\rm K}(t)$ consists of two Dirac delta functions. |
| − | - $h_{\rm K}(t)$ | + | - $h_{\rm K}(t)$ is complex-valued. |
| − | - $h_{\rm K}(t)$ | + | - $h_{\rm K}(t)$ is a function periodic with the delay time $\tau$ . |
| − | { | + | {What statements hold for the channel frequency response $H_{\rm K}(f)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It holds $H_{\rm K}(f = 0) = 2$. |
| − | + $H_{\rm K}(f)$ | + | + $H_{\rm K}(f)$ is complex-valued. |
| − | + $|H_{\rm K}(f)|$ | + | + $|H_{\rm K}(f)|$ is a function periodic with frequency $1/ \tau$ . |
| − | { | + | {Set $K = 1, \ h_{0} = 0.6$ and $h_{1} = 0.4$. Determine the delays $\tau_{0}$ and $\tau_{1}$ so that the $h_{\rm KR}(t)$ equation is satisfied with $A_{0} = A_{2}$ . |
|type="{}"} | |type="{}"} | ||
$\tau_{0} \ = \ $ { 1 3% } $\ \rm µ s$ | $\tau_{0} \ = \ $ { 1 3% } $\ \rm µ s$ | ||
$\tau_{1} \ = \ $ { 0 3% } $\ \rmµ s$ | $\tau_{1} \ = \ $ { 0 3% } $\ \rmµ s$ | ||
| − | { | + | {What value to choose for the constant $K$ ? |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 1.923 3% } | $K \ = \ $ { 1.923 3% } | ||
| − | { | + | {What statements hold for the signals $r(t)$ and $b(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The maximum value of $r(t)$ is $1$. |
| − | - | + | - The width of $r(t)$ is $7 \ \rm µ s$. |
| − | - | + | - The maximum value of $b(t)$ is $1 \ \rm µ s$. |
| − | + | + | + The width of $b(t)$ is $7 \ \rm µ s$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is <u>solution 1</u>: |
| − | * | + | *The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when a dirac impulse is present at the input $\Rightarrow s(t) = \delta(t)$. |
| − | * | + | * From this follows: |
:$$h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$ | :$$h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Correct are <u>solutions 2 and 3</u>: |
| − | * | + | *The channel frequency response $H_{\rm K}(f)$ is by definition the Fourier transform of the impulse response $h_{\rm K}(t)$. Using the displacement theorem, this results in: |
:$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$ | :$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$ | ||
| − | * | + | *The first proposed solution is accordingly wrong in contrast to the other two: |
| − | *$H_{\rm K}(f)$ | + | *$H_{\rm K}(f)$ is complex-valued and the magnitude is periodic with $1/\tau$, as the following calculation shows: |
| − | :$$|H_{\rm K}(f)|^2 | + | :$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0. 4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$ |
:$$\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = \sqrt { 0.52 + 0.48 \cdot \cos(2 \pi f \tau) } \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = \sqrt { 0.52 + 0.48 \cdot \cos(2 \pi f \tau) } \hspace{0.05cm}.$$ | ||
| − | * | + | *For $f = 0$ is $|H_{\rm K}(f)| = 1$. At the respective frequency interval $1/\tau$ this value repeats. |
| − | '''(3)''' | + | '''(3)''' We first set $K = 1$ as agreed. In total, there are four ways to get from $s(t)$ to the output signal $b(t)$. |
| − | * | + | *To satisfy the given $h_{\rm KR}(t)$ equation, either $\tau_{0} = 0$ must hold or $\tau_{1}= 0$. With $\tau_{0} = 0$ we obtain for the impulse response: |
| − | :$$ h_{\rm KR}(t) \ = \ 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$ | + | :$$ h_{\rm KR}(t) \ = \ 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0. 6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$ |
| − | * | + | *To be able to concentrate the "main energy" on a time point, then $\tau_{1} = \tau$ would have to be chosen. With $h_{0} = 0.6$ and $h_{1} = 0.4$ one then gets $A_{0} \neq A_{2}$: |
:$$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) \hspace{-0.05cm}+\hspace{-0.05cm}0.48 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | :$$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) \hspace{-0.05cm}+\hspace{-0.05cm}0.48 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | ||
| − | * | + | *In contrast, with $h_{0} = 0.6$, $h_{1} = 0.4, \tau_{0} = \tau$ und $\tau_{1} = 0$: |
:$$h_{\rm KR}(t)= 0.6 \cdot h_0 \cdot \delta (t - \tau ) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_0 \cdot \delta (t - 2\tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.6 \cdot h_1 \cdot \delta (t) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.52 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.24 \cdot \big[ \delta (t ) +\delta (t - 2\tau)\big] \hspace{0.05cm}.$$ | :$$h_{\rm KR}(t)= 0.6 \cdot h_0 \cdot \delta (t - \tau ) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_0 \cdot \delta (t - 2\tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.6 \cdot h_1 \cdot \delta (t) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.52 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.24 \cdot \big[ \delta (t ) +\delta (t - 2\tau)\big] \hspace{0.05cm}.$$ | ||
| − | * | + | *Here the additional condition $A_{0} = A_{2}$ is satisfied. Thus, the result we are looking for is: |
:$$\tau_0 = \tau \hspace{0.15cm}\underline {= 1\,{\rm µ s}} \hspace{0.05cm},\hspace{0.2cm}\tau_1 \hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$ | :$$\tau_0 = \tau \hspace{0.15cm}\underline {= 1\,{\rm µ s}} \hspace{0.05cm},\hspace{0.2cm}\tau_1 \hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' It holds according to the given equation. |
:$$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52}\hspace{0.15cm}\underline { \approx 1.923 } \hspace{0.05cm}.$$ | :$$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52}\hspace{0.15cm}\underline { \approx 1.923 } \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, for the joint impulse response (it holds $0.24/0.52 = 6/13$) we obtain: |
:$$h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | :$$h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' For the received signal $r(t)$ and for the RAKE output signal $b(t)$ hold: |
| − | [[File:P_ID1980__Mod_Z_5_5e.png|right|frame| | + | [[File:P_ID1980__Mod_Z_5_5e.png|right|frame|Signals to illustrate the RAKE receiver]] |
| − | :$$ r(t) | + | :$$ r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm \mu s})\hspace{0.05cm},$$ |
| − | :$$ b(t) | + | :$$ b(t) = \frac{6}{13} \cdot s(t) \hspace{-0.05cm} + \hspace{-0.05cm} 1.00 \cdot s (t \hspace{-0.05cm} - \hspace{-0.05cm}1\,{\rm \mu s}) \hspace{-0.05cm}+ \hspace{-0.05cm}\frac{6}{13} \cdot s (t \hspace{-0.05cm}- \hspace{-0.05cm} 2\,{\rm \mu s}) \hspace{0.05cm}.$$ |
| − | + | Correct are <u>statements 1 and 4</u>, as the graph shows. | |
| − | + | Regarding the AWGN noise behavior, $r(t)$ and $b(t)$ are comparable. | |
| Line 125: | Line 125: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^4.3 Telecommunications Aspects |
^]] | ^]] | ||
Latest revision as of 13:28, 3 March 2023
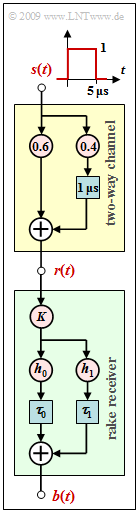
The graphic shows a two-way channel (yellow background). The corresponding description equation is:
- $$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$
Let the delay on the side path be $\tau = 1 \ \rm µ s$. Drawn below is the structure of a RAKE receiver (green background) with general coefficients $K, \ h_{0}, \ h_{1}, \ \tau_{0}$ and $\tau_{1}$.
The RAKE receiver has the task of combining the energy of the two signal paths to make the decision more reliable. The joint impulse response of the channel and the RAKE receiver can be expressed in the form
- $$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$
can be given, but only if the RAKE coefficients $h_{0}, \ h_{1}, \ \tau_{0}$ and $\tau_{1}$ are appropriately chosen. The main part of $h_{\rm KR}(t)$ shall be at $t = \tau$ .
The constant $K$ is necessary for normalization reasons. In order not to distort the influence of AWGN noise, the following condition must be fulfilled:
- $$K= \frac{1}{h_0^2 + h_1^2}.$$
Besides the appropriate RAKE parameters, the signals $r(t)$ and $b(t)$ are also sought if $s(t)$ describes a rectangle of height $1$ and width $T = 5 \ \rm µ s$ .
Hints:
- The task belongs to the chapter "Telecommunications Aspects of UMTS".
- Reference is also made to the page "Examinations of the rake receiver" in the book "Modulation Methods".
Questions
Solution
(1) Correct is solution 1:
- The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when a dirac impulse is present at the input $\Rightarrow s(t) = \delta(t)$.
- From this follows:
- $$h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$
(2) Correct are solutions 2 and 3:
- The channel frequency response $H_{\rm K}(f)$ is by definition the Fourier transform of the impulse response $h_{\rm K}(t)$. Using the displacement theorem, this results in:
- $$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$
- The first proposed solution is accordingly wrong in contrast to the other two:
- $H_{\rm K}(f)$ is complex-valued and the magnitude is periodic with $1/\tau$, as the following calculation shows:
- $$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0. 4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$
- $$\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = \sqrt { 0.52 + 0.48 \cdot \cos(2 \pi f \tau) } \hspace{0.05cm}.$$
- For $f = 0$ is $|H_{\rm K}(f)| = 1$. At the respective frequency interval $1/\tau$ this value repeats.
(3) We first set $K = 1$ as agreed. In total, there are four ways to get from $s(t)$ to the output signal $b(t)$.
- To satisfy the given $h_{\rm KR}(t)$ equation, either $\tau_{0} = 0$ must hold or $\tau_{1}= 0$. With $\tau_{0} = 0$ we obtain for the impulse response:
- $$ h_{\rm KR}(t) \ = \ 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0. 6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$
- To be able to concentrate the "main energy" on a time point, then $\tau_{1} = \tau$ would have to be chosen. With $h_{0} = 0.6$ and $h_{1} = 0.4$ one then gets $A_{0} \neq A_{2}$:
- $$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) \hspace{-0.05cm}+\hspace{-0.05cm}0.48 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
- In contrast, with $h_{0} = 0.6$, $h_{1} = 0.4, \tau_{0} = \tau$ und $\tau_{1} = 0$:
- $$h_{\rm KR}(t)= 0.6 \cdot h_0 \cdot \delta (t - \tau ) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_0 \cdot \delta (t - 2\tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.6 \cdot h_1 \cdot \delta (t) \hspace{-0.05cm}+\hspace{-0.05cm} 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.52 \cdot \delta (t - \tau) \hspace{-0.05cm}+\hspace{-0.05cm} 0.24 \cdot \big[ \delta (t ) +\delta (t - 2\tau)\big] \hspace{0.05cm}.$$
- Here the additional condition $A_{0} = A_{2}$ is satisfied. Thus, the result we are looking for is:
- $$\tau_0 = \tau \hspace{0.15cm}\underline {= 1\,{\rm µ s}} \hspace{0.05cm},\hspace{0.2cm}\tau_1 \hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$
(4) It holds according to the given equation.
- $$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52}\hspace{0.15cm}\underline { \approx 1.923 } \hspace{0.05cm}.$$
- Thus, for the joint impulse response (it holds $0.24/0.52 = 6/13$) we obtain:
- $$h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
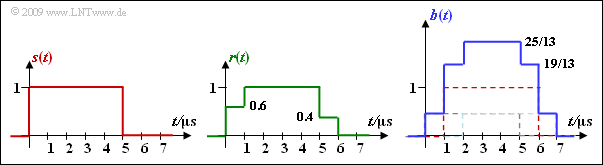
(5) For the received signal $r(t)$ and for the RAKE output signal $b(t)$ hold:
- $$ r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm \mu s})\hspace{0.05cm},$$
- $$ b(t) = \frac{6}{13} \cdot s(t) \hspace{-0.05cm} + \hspace{-0.05cm} 1.00 \cdot s (t \hspace{-0.05cm} - \hspace{-0.05cm}1\,{\rm \mu s}) \hspace{-0.05cm}+ \hspace{-0.05cm}\frac{6}{13} \cdot s (t \hspace{-0.05cm}- \hspace{-0.05cm} 2\,{\rm \mu s}) \hspace{0.05cm}.$$
Correct are statements 1 and 4, as the graph shows.
Regarding the AWGN noise behavior, $r(t)$ and $b(t)$ are comparable.