Difference between revisions of "Aufgaben:Exercise 1.8: Variable Edge Steepness"
| (42 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
| − | [[File: | + | [[File:EN_LZI_A_1_8.png|right|frame|Trapezoidal low-pass filter (red) and raised-cosine low-pass filter (green)]] |
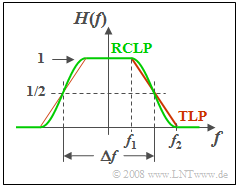
| − | + | Two low-pass filters with variable edge steepnesses are compared with each other. For frequencies $|f| ≤ f_1$ , $H(f) = 1$ holds in both cases. In contrast, all frequencies $|f| ≥ f_2$ are suppressed entirely. | |
| − | + | In the range $f_1 ≤ |f| ≤ f_2$ the frequency responses are defined by the following equations: | |
| − | * | + | *Trapezoidal low-pass filter $\rm (TLP)$: |
:$$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$ | :$$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$ | ||
| − | * | + | *Raised-cosine low-pass filter $\rm (RCLP)$: |
:$$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$ | :$$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$ | ||
| − | Alternative | + | Alternative system parameters for both low-pass filters are |
| − | * | + | *the equivalent bandwidth $Δf$ defined by the equal-area rectangle, and also |
| − | * | + | *the roll-off factor (in frequency domain): |
:$$r=\frac{f_2 - f_1}{f_2 + f_1} .$$ | :$$r=\frac{f_2 - f_1}{f_2 + f_1} .$$ | ||
| − | + | Throughout the task, $Δf = 10 \ \rm kHz$ and $r = 0.2$ hold true. | |
| − | + | The impulse responses are with the equivalent impulse duration $Δt = 1/Δf = 0.1 \ \rm ms$: | |
:$$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot | :$$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot | ||
\frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$ | \frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$ | ||
| Line 31: | Line 31: | ||
| − | '' | + | ''Please note:'' |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. |
| − | * | + | *In particular, reference is made to the pages [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Trapezoidal_low-pass_filter|Trapezoidal low-pass filter]] and [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Raised-cosine_low-pass_filter|Raised-cosine low-pass filter]]. |
| − | * | + | *You can check your results with the interactive applet [[Applets:Frequenzgang_und_Impulsantwort|Frequency response and impulse response]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the equation for the equivalent bandwidth $Δf$? It holds that |
|type="[]"} | |type="[]"} | ||
- $Δf = f_2 - f_1$, | - $Δf = f_2 - f_1$, | ||
| Line 48: | Line 48: | ||
| − | { | + | {Determine the low-pass filter parameters $f_1$ and $f_2$ for $Δf = 10 \ \rm kHz$ and $r = 0.2$. |
|type="{}"} | |type="{}"} | ||
$f_1 \ = \ $ { 4 3% } $\ \rm kHz$ | $f_1 \ = \ $ { 4 3% } $\ \rm kHz$ | ||
| Line 54: | Line 54: | ||
| − | { | + | {Which statements are true for the impulse response of the trapezoidal low-pass filter if $r = 0.2$ is assumed? |
|type="[]"} | |type="[]"} | ||
| − | + $h(t)$ | + | + $h(t)$ has zeros at $±\hspace{0.03cm}n · Δt \ (n = 1, 2, \text{...})$. |
| − | - $h(t)$ | + | - $h(t)$ has additional zeros at other times. |
| − | - | + | - $h(t)$ would decay faster with $r = 0$ . |
| − | + | + $h(t)$ would decay faster with $r = 1$ . | |
| − | { | + | {Which statements are true for the impulse response of the raised-cosine low-pass filter if $r = 0.2$ is assumed? |
|type="[]"} | |type="[]"} | ||
| − | + $h(t)$ | + | + $h(t)$ has zeros at $±\hspace{0.03cm}n · Δt \ (n = 1, 2, \text{...})$. |
| − | + $h(t)$ | + | + $h(t)$ has additional zeros at other times. |
| − | - | + | - $h(t)$ would decay faster with $r = 0$ . |
| − | + | + $h(t)$ would decay faster with $r = 1$ . | |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Approach 2</u> is correct: |
| − | * | + | *For both low-pass filters, the integral over $H(f)$ is equal to $f_1 + f_2$. |
| + | *Thus, due to $H(f = 0 = 1)$ <u>Approach 2</u> is correct: $\Delta f = f_1 + f_2.$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' Substituting the relation found in '''(1)''' into the defining equation of the roll-off factor the following is obtained: | ||
:$${f_2 - f_1} = r \cdot \Delta f = {2\,\rm | :$${f_2 - f_1} = r \cdot \Delta f = {2\,\rm | ||
kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm | kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm | ||
kHz}.$$ | kHz}.$$ | ||
| − | + | *By addition or subtraction of both equations the so-called "corner frequencies" result in | |
| + | :$$f_1 \underline{= 4 \ \rm kHz},$$ | ||
| + | :$$f_2 \underline{= 6 \ \rm kHz}.$$ | ||
| − | '''(3)''' | + | '''(3)''' <u>Suggestions 1 and 4</u> are correct: |
| − | * | + | *The first $\rm sinc$–function of $h_{\rm TTP}(t)$ causes zeros at an interval of $\Delta t$ (see also the equation on the information page). |
| − | * | + | *The second $\rm sinc$–function causes zeros at multiples of $5 · \Delta t$. |
| − | * | + | *There are no additional zeros since these coincide exactly with the zeros of the first $\rm sinc$–function. |
| − | * | + | *The special case $r = 0$ corresponds to the ideal rectangular low-pass filter with $\rm sinc$–shaped impulse response. This decays extremely slowly. |
| − | * | + | *The $\rm si^2$–shaped impulse response of the triangular low-pass filter $($special case for $r = 1)$ decays asymptotically with $1/t^2$, i.e. faster than with $r = 0.2$. |
| − | '''(4)''' | + | '''(4)''' <u>Suggestions 1, 2 and 4</u> are correct here: |
| − | * | + | *The impulse response $h_{\rm CRTP}(t)$ of the raised-cosine low-pass filter also has zeros at an interval of $\Delta t$ due to the $\rm sinc$–function. |
| − | * | + | *The cosine function has zeros at the following times: |
:$${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm | :$${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm | ||
0.5, \pm 1.5, \pm 2.5, \text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm | 0.5, \pm 1.5, \pm 2.5, \text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm | ||
| Line 102: | Line 106: | ||
:$$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm | :$$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm | ||
2.5, \pm 7.5, \pm 12.5, \text{...}. $$ | 2.5, \pm 7.5, \pm 12.5, \text{...}. $$ | ||
| − | * | + | *However, the zero of the numerator at $t / \Delta t = 2.5$ is nullified by the denominator which also vanishes. |
| − | * | + | *By contrast, the other zeros at $7.5, 12.5,\text{...} $ remain. |
| − | * | + | *Here, $r = 0$ also results in the rectangular low-pass filter and thus in the $\rm sinc$–shaped impulse response. |
| − | * | + | *In contrast, the impulse response of the cosine-square low-pass filter $($special case for $r = 1)$ decays extremely fast. |
| − | * | + | *This is studied in detail in [[Aufgaben:Exercise_1.8Z:_Cosine-Square_Low-Pass|Exercise 1.8Z]] . |
| Line 113: | Line 117: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.3 Some Low-Pass Functions in Systems Theory^]] |
Latest revision as of 15:19, 7 October 2021
Two low-pass filters with variable edge steepnesses are compared with each other. For frequencies $|f| ≤ f_1$ , $H(f) = 1$ holds in both cases. In contrast, all frequencies $|f| ≥ f_2$ are suppressed entirely.
In the range $f_1 ≤ |f| ≤ f_2$ the frequency responses are defined by the following equations:
- Trapezoidal low-pass filter $\rm (TLP)$:
- $$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$
- Raised-cosine low-pass filter $\rm (RCLP)$:
- $$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$
Alternative system parameters for both low-pass filters are
- the equivalent bandwidth $Δf$ defined by the equal-area rectangle, and also
- the roll-off factor (in frequency domain):
- $$r=\frac{f_2 - f_1}{f_2 + f_1} .$$
Throughout the task, $Δf = 10 \ \rm kHz$ and $r = 0.2$ hold true.
The impulse responses are with the equivalent impulse duration $Δt = 1/Δf = 0.1 \ \rm ms$:
- $$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$
- $$h_{\rm CRTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the pages Trapezoidal low-pass filter and Raised-cosine low-pass filter.
- You can check your results with the interactive applet Frequency response and impulse response.
Questions
Solution
- For both low-pass filters, the integral over $H(f)$ is equal to $f_1 + f_2$.
- Thus, due to $H(f = 0 = 1)$ Approach 2 is correct: $\Delta f = f_1 + f_2.$
(2) Substituting the relation found in (1) into the defining equation of the roll-off factor the following is obtained:
- $${f_2 - f_1} = r \cdot \Delta f = {2\,\rm kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm kHz}.$$
- By addition or subtraction of both equations the so-called "corner frequencies" result in
- $$f_1 \underline{= 4 \ \rm kHz},$$
- $$f_2 \underline{= 6 \ \rm kHz}.$$
(3) Suggestions 1 and 4 are correct:
- The first $\rm sinc$–function of $h_{\rm TTP}(t)$ causes zeros at an interval of $\Delta t$ (see also the equation on the information page).
- The second $\rm sinc$–function causes zeros at multiples of $5 · \Delta t$.
- There are no additional zeros since these coincide exactly with the zeros of the first $\rm sinc$–function.
- The special case $r = 0$ corresponds to the ideal rectangular low-pass filter with $\rm sinc$–shaped impulse response. This decays extremely slowly.
- The $\rm si^2$–shaped impulse response of the triangular low-pass filter $($special case for $r = 1)$ decays asymptotically with $1/t^2$, i.e. faster than with $r = 0.2$.
(4) Suggestions 1, 2 and 4 are correct here:
- The impulse response $h_{\rm CRTP}(t)$ of the raised-cosine low-pass filter also has zeros at an interval of $\Delta t$ due to the $\rm sinc$–function.
- The cosine function has zeros at the following times:
- $${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm 0.5, \pm 1.5, \pm 2.5, \text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, ... $$
- $$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, \text{...}. $$
- However, the zero of the numerator at $t / \Delta t = 2.5$ is nullified by the denominator which also vanishes.
- By contrast, the other zeros at $7.5, 12.5,\text{...} $ remain.
- Here, $r = 0$ also results in the rectangular low-pass filter and thus in the $\rm sinc$–shaped impulse response.
- In contrast, the impulse response of the cosine-square low-pass filter $($special case for $r = 1)$ decays extremely fast.
- This is studied in detail in Exercise 1.8Z .