Difference between revisions of "Aufgaben:Exercise 3.2Z: Two-dimensional Probability Mass Function"
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables |
}} | }} | ||
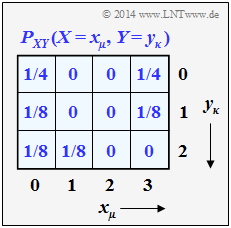
| − | [[File:P_ID2752__Inf_Z_3_2_neu.png|right|frame| | + | [[File:P_ID2752__Inf_Z_3_2_neu.png|right|frame|$\rm PMF$ of the two-dimensional random variable $XY$]] |
| − | + | We consider the random variables $X = \{ 0,\ 1,\ 2,\ 3 \}$ and $Y = \{ 0,\ 1,\ 2 \}$, whose joint probability mass function $P_{XY}(X,\ Y)$ is given. | |
| − | * | + | *From this two-dimensional probability mass function $\rm (PMF)$, the one-dimensional probability mass functions $P_X(X)$ and $P_Y(Y)$ are to be determined. |
| − | * | + | *Such a one-dimensional probability mass function is sometimes also called "marginal probability". |
| − | + | If $P_{XY}(X,\ Y) = P_X(X) \cdot P_Y(Y)$, the two random variables $X$ and $Y$ are statistically independent. Otherwise, there are statistical dependencies between them. | |
| − | + | In the second part of the task we consider the random variables $U= \big \{ 0,\ 1 \big \}$ and $V= \big \{ 0,\ 1 \big \}$, which result from $X$ and $Y$ by modulo-2 operations: | |
:$$U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2, \hspace{0.3cm} V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2.$$ | :$$U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2, \hspace{0.3cm} V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2.$$ | ||
| Line 22: | Line 22: | ||
| − | + | <u>Hints:</u> | |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Some preliminary remarks on two-dimensional random variables]]. |
| − | * | + | *The same constellation is assumed here as in [[Aufgaben:Aufgabe_3.2:_Erwartungswertberechnungen|Exercise 3.2]]. |
| − | * | + | *There the random variables $Y = \{ 0,\ 1,\ 2,\ 3 \}$ were considered, but with the addition ${\rm Pr}(Y = 3) = 0$. |
| − | * | + | *The property $|X| = |Y|$ forced in this way was advantageous in the previous task for the formal calculation of the expected value. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the probability mass function $P_X(X)$? |
|type="{}"} | |type="{}"} | ||
$P_X(0) \ = \ $ { 0.5 3% } | $P_X(0) \ = \ $ { 0.5 3% } | ||
| Line 41: | Line 41: | ||
$P_X(3) \ = \ ${ 0.375 3% } | $P_X(3) \ = \ ${ 0.375 3% } | ||
| − | { | + | {What is the probability mass function $P_Y(Y)$? |
|type="{}"} | |type="{}"} | ||
$P_Y(0) \ = \ $ { 0.5 3% } | $P_Y(0) \ = \ $ { 0.5 3% } | ||
| Line 47: | Line 47: | ||
$P_Y(2) \ = \ $ { 0.25 3% } | $P_Y(2) \ = \ $ { 0.25 3% } | ||
| − | { | + | {Are the random variables $X$ and $Y$ statistically independent? |
| + | |||
|type="()"} | |type="()"} | ||
| − | - | + | - Yes, |
| − | + | + | + No. |
| − | { | + | {Determine the probabilities $P_{UV}( U,\ V)$. |
|type="{}"} | |type="{}"} | ||
$P_{UV}( U = 0,\ V = 0) \ = \ $ { 0.375 3% } | $P_{UV}( U = 0,\ V = 0) \ = \ $ { 0.375 3% } | ||
| Line 60: | Line 61: | ||
$P_{UV}( U =1,\ V = 1) \ = \ $ { 0.125 3% } | $P_{UV}( U =1,\ V = 1) \ = \ $ { 0.125 3% } | ||
| − | { | + | {Are the random variables $U$ and $V$ statistically independent? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
| Line 69: | Line 70: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' You get from $P_{XY}(X,\ Y)$ to the one-dimensional probability mass function $P_X(X)$ by summing up all $Y$ probabilities: |
:$$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$ | :$$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$ | ||
| − | + | *One thus obtains the following numerical values: | |
:$$P_X(X = 0) = 1/4+1/8+1/8 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$ | :$$P_X(X = 0) = 1/4+1/8+1/8 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$ | ||
:$$P_X(X = 1)= 0+0+1/8 = 1/8 \hspace{0.15cm}\underline{= 0.125},$$ | :$$P_X(X = 1)= 0+0+1/8 = 1/8 \hspace{0.15cm}\underline{= 0.125},$$ | ||
| Line 80: | Line 81: | ||
| − | '''(2)''' | + | |
| + | '''(2)''' Analogous to sub-task '''(1)''' , the following now holds: | ||
:$$P_Y(Y = y_{\kappa}) = \sum_{x \hspace{0.05cm} \in \hspace{0.05cm} X} \hspace{0.1cm} P_{XY}(x, y_{\kappa})$$ | :$$P_Y(Y = y_{\kappa}) = \sum_{x \hspace{0.05cm} \in \hspace{0.05cm} X} \hspace{0.1cm} P_{XY}(x, y_{\kappa})$$ | ||
:$$P_Y(Y= 0) = 1/4+0+0+1/4 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$ | :$$P_Y(Y= 0) = 1/4+0+0+1/4 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$ | ||
| Line 87: | Line 89: | ||
| − | |||
| + | '''(3)''' With statistical independence, $P_{XY}(X,Y)= P_X(X) \cdot P_Y(Y)$ should be. | ||
| + | *This does not apply here: answer <u>'''NO'''</u>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Starting from the left-hand table ⇒ $P_{XY}(X,Y)$, we arrive at the middle table ⇒ $P_{UY}(U,Y)$, <br>by combining certain probabilities according to $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$. | ||
| − | + | If one also takes into account $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$, one obtains the probabilities sought according to the right-hand table: | |
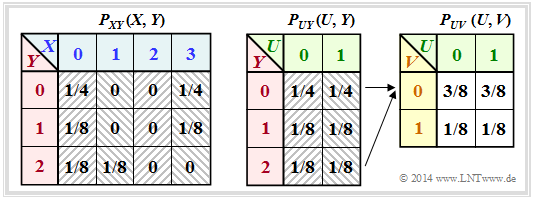
| + | [[File:P_ID2753__Inf_Z_3_2d_neu.png|right|frame|Different probability functions]] | ||
| − | + | :$$P_{UV}( U = 0, V = 0) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | |
| + | :$$P_{UV}( U = 0, V = 1) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | ||
| + | :$$P_{UV}( U = 1, V = 0) = 1/8 \hspace{0.15cm}\underline{= 0.125},$$ | ||
| + | :$$P_{UV}( U = 1, V = 1) = 1/8 \hspace{0.15cm}\underline{= 0.125}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' | + | '''(5)''' The correct answer is <u>'''YES'''</u>: |
| − | * | + | *The corresponding one-dimensional probability mass functions are: |
| − | * | + | :$$P_U(U) = \big [1/2 , \ 1/2 \big ],$$ |
| + | :$$P_V(V)=\big [3/4, \ 1/4 \big ].$$ | ||
| + | *Thus: $P_{UV}(U,V) = P_U(U) \cdot P_V(V)$ ⇒ $U$ and $V$ are statistically independent. | ||
| Line 117: | Line 125: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.1 General Information on 2D Random Variables^]] |
Latest revision as of 09:12, 24 September 2021
We consider the random variables $X = \{ 0,\ 1,\ 2,\ 3 \}$ and $Y = \{ 0,\ 1,\ 2 \}$, whose joint probability mass function $P_{XY}(X,\ Y)$ is given.
- From this two-dimensional probability mass function $\rm (PMF)$, the one-dimensional probability mass functions $P_X(X)$ and $P_Y(Y)$ are to be determined.
- Such a one-dimensional probability mass function is sometimes also called "marginal probability".
If $P_{XY}(X,\ Y) = P_X(X) \cdot P_Y(Y)$, the two random variables $X$ and $Y$ are statistically independent. Otherwise, there are statistical dependencies between them.
In the second part of the task we consider the random variables $U= \big \{ 0,\ 1 \big \}$ and $V= \big \{ 0,\ 1 \big \}$, which result from $X$ and $Y$ by modulo-2 operations:
- $$U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2, \hspace{0.3cm} V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2.$$
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- The same constellation is assumed here as in Exercise 3.2.
- There the random variables $Y = \{ 0,\ 1,\ 2,\ 3 \}$ were considered, but with the addition ${\rm Pr}(Y = 3) = 0$.
- The property $|X| = |Y|$ forced in this way was advantageous in the previous task for the formal calculation of the expected value.
Questions
Solution
- $$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$
- One thus obtains the following numerical values:
- $$P_X(X = 0) = 1/4+1/8+1/8 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$
- $$P_X(X = 1)= 0+0+1/8 = 1/8 \hspace{0.15cm}\underline{= 0.125},$$
- $$P_X(X = 2) = 0+0+0 \hspace{0.15cm}\underline{= 0}$$
- $$P_X(X = 3) = 1/4+1/8+0=3/8 \hspace{0.15cm}\underline{= 0.375}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} P_X(X) = \big [ 1/2, \ 1/8 , \ 0 , \ 3/8 \big ].$$
(2) Analogous to sub-task (1) , the following now holds:
- $$P_Y(Y = y_{\kappa}) = \sum_{x \hspace{0.05cm} \in \hspace{0.05cm} X} \hspace{0.1cm} P_{XY}(x, y_{\kappa})$$
- $$P_Y(Y= 0) = 1/4+0+0+1/4 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$
- $$P_Y(Y = 1) = 1/8+0+0+1/8 = 1/4 \hspace{0.15cm}\underline{= 0.250},$$
- $$P_Y(Y = 2) = 1/8+1/8+0+0 = 1/4 \hspace{0.15cm}\underline{= 0.250} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} P_Y(Y= 0) = \big [ 1/2, \ 1/4 , \ 1/4 ].$$
(3) With statistical independence, $P_{XY}(X,Y)= P_X(X) \cdot P_Y(Y)$ should be.
- This does not apply here: answer NO.
(4) Starting from the left-hand table ⇒ $P_{XY}(X,Y)$, we arrive at the middle table ⇒ $P_{UY}(U,Y)$,
by combining certain probabilities according to $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$.
If one also takes into account $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$, one obtains the probabilities sought according to the right-hand table:
- $$P_{UV}( U = 0, V = 0) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$
- $$P_{UV}( U = 0, V = 1) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$
- $$P_{UV}( U = 1, V = 0) = 1/8 \hspace{0.15cm}\underline{= 0.125},$$
- $$P_{UV}( U = 1, V = 1) = 1/8 \hspace{0.15cm}\underline{= 0.125}.$$
(5) The correct answer is YES:
- The corresponding one-dimensional probability mass functions are:
- $$P_U(U) = \big [1/2 , \ 1/2 \big ],$$
- $$P_V(V)=\big [3/4, \ 1/4 \big ].$$
- Thus: $P_{UV}(U,V) = P_U(U) \cdot P_V(V)$ ⇒ $U$ and $V$ are statistically independent.