Difference between revisions of "Aufgaben:Exercise 1.6Z: Comparison of Rayleigh and Rice"
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Mobile Kommunikation/Nichtfrequenzselektives Fading mit Direktkomponente}} Datei:P_ID2135__Mob_Z_1_6.png|right|frame|Phasendiagramm…“) |
|||
| (35 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Non-Frequency_Selective_Fading_With_Direct_Component}} |
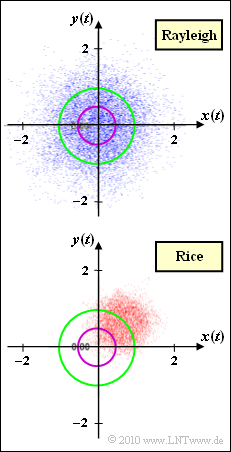
| + | [[File:P_ID2135__Mob_Z_1_6.png|right|frame|Phase diagram of the factor $z(t) = x(t) + {\rm j} \cdot y(t)$ <br>for Rayleigh and Rice fading]] | ||
| − | + | In this task "Rayleigh fading" and "Rice fading" are to be compared with each other. | |
| − | In | ||
| − | + | The graph shows the complex factor $z(t) = x(t) + {\rm j} \cdot y(t)$ in the complex plane. For the low-pass transmission signal $s(t) = 1$ $($which with respect to a band-pass system corresponds to a cosine oscillation with amplitude $1)$, the low-pass reception signal is $r(t)=z(t)$. | |
| − | * | + | *The upper diagram describes [[Mobile_Communications/Probability_Density_of_Rayleigh_Fading| Rayleigh fading]], where the component signals $x(t)$ and $y(t)$ are each Gaussian distributed with variance $\sigma^2$. For $a ≥ 0$, the probability density function of the magnitude $a(t) = |z(t)|$ is: |
| − | :$$f_a(a) = | + | :$$f_a(a) = {a}/{\sigma^2} \cdot {\rm e}^{ -{a^2 }/({2\sigma^2})} \hspace{0.05cm}.$$ |
| − | : | + | :The noncentral second moment ("power") of $z(t)$ is $1$: |
:$${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.3cm} | :$${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} | \Rightarrow \hspace{0.3cm} | ||
| Line 15: | Line 15: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The lower phase diagram is the result of [[Mobile_Communications/Non-Frequency_Selective_Fading_With_Direct_Component#Example_of_signal_behaviour_with_Rice_fading|Rice fading]]. Here, too, $x(t)$ and $y(t)$ are Gaussian distributed with variance $\sigma^2$, but now with mean value $x_0$ and $y_0$. The PDF for $a ≥ 0$ is |
| − | :$$f_a(a) = | + | :$$f_a(a) ={a}/{\sigma^2} \cdot {\rm e}^{ -{(a^2+ |z_0|^2) }/({2\sigma^2})}\cdot {\rm I}_0 \left [ {a \cdot |z_0|}/{\sigma^2} \right ]\hspace{0.05cm}.$$ |
| − | + | :where ${\rm I}_0$ is the modified Bessel function of the first kind. The power now includes the contribution of the direct component $z_0 = x_0 + {\rm j} \cdot y_0$: | |
| − | : | ||
:$${\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$ | :$${\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$ | ||
| − | + | For the system comparison | |
| − | * | + | * the second moment is assumed to be constant: ${\rm E}\big[|z(t)|^2\big] = 1$, |
| − | * | + | * the Rice fading is based on the direction shown in the graph, |
| − | * | + | * let the power be split between the direct path $(|z_0|^2)$ and the scattering paths $(2\sigma^2)$ in the ratio $4:1$ . |
| − | + | For the subtasks '''(1)''' to '''(4)''', let $s(t) = 1$. For the subtasks '''(5)''' and '''(6)''', a BPSK signal is assumed . The low-pass signal $s(t)$ thus has a rectangular shape with the possible values $±1$. The duration of each rectangular impulse is $T = 10 \ \rm ms$. | |
| Line 35: | Line 34: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * This task belongs to chapter [[Mobile_Communications/Non-frequency_selective_fading_with_direct_component|Non-frequency selective fading with direct component]]. |
| − | * | + | * The circles drawn in the graph (violet and green) refer to the subtasks '''(3)''' and '''(4)'''. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {When does the Rice model result in an ideal channel ⇒ $H(f) = 1$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - With $x_0 = y_0 = 0, \ \ \sigma^2 = 1$. |
| − | + | + | + With $x_0 = 1, \ \ y_0 = 0, \ \ \ \sigma^2 = 0$. |
| − | - | + | - With $x_0 = 0, \ \ \ y_0 = 1, \ \ \ \sigma^2 = 0$. |
| − | { | + | {Determine the Rice parameters using the given assumptions and the graph. |
|type="{}"} | |type="{}"} | ||
$\sigma \ = \ $ { 0.316 3% } | $\sigma \ = \ $ { 0.316 3% } | ||
| Line 56: | Line 55: | ||
$y_0 \ = \ $ { 0.632 3% } | $y_0 \ = \ $ { 0.632 3% } | ||
| − | { | + | {For which channel is ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ -6 \ \ \rm dB)$ larger? |
|type="()"} | |type="()"} | ||
| − | + | + | + The Rayleigh channel. |
| − | - | + | - The Rice channel. |
| − | - | + | - The probabilities are approximately equal. |
| − | { | + | {For which channel is ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ 0 \ \ \rm dB)$ larger? |
|type="()"} | |type="()"} | ||
| − | - | + | - The Rayleigh channel. |
| − | - | + | - The Rice channel. |
| − | + | + | + The probabilities are approximately equal. |
| − | { | + | {Which statements apply to a BPSK transmission signal $s(t)$ when considering the complex representation of the received signal $r(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - Rayleigh | + | - Rayleigh fading causes point clouds in quadrants $1$ and $3$. |
| − | + Rice | + | + Rice fading causes point clouds in quadrants $1$ and $3$. |
| − | + | + | + For Rayleigh, the PDF of $|r(t)|$ is equal to the PDF of $|z(t)|$. |
| − | - | + | - For Rice, the PDF of $|r(t)|$ is equal to the PDF of $|z(t)|$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solution 2</u> is correct: |
| − | * | + | *The first suggestion corresponds to a Rayleigh fading model. With the last setting, we would have |
:$$|z(t)| = {\rm j} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \cdot z(t) = {\rm j} \cdot s(t) | :$$|z(t)| = {\rm j} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \cdot z(t) = {\rm j} \cdot s(t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *If we take into account that we are in the equivalent low-pass range, then a cosine input would produce a negative sinusoidal band-pass signal $r_{\rm BP}(t)$. |
| − | * | + | *On the other hand, solution 2 applies to all possible signals: |
| − | :$$|z(t)| = x_0 = 1 | + | :$$|z(t)| = x_0 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' For the given Rayleigh fading, we have $\sigma^2 = 0.5$. For the second moment of the multiplicative factor $z(t)$, this results in: |
| − | :$${\rm E}\left [ |z(t)|^2 \right ] = 2 | + | :$${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The Rice fading should have exactly the same performance. That is, it should apply: | |
| − | :$$|z_0|^2 + 2 | + | :$$|z_0|^2 + 2 \sigma^2 = 1 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Furthermore, it was requested: | |
| − | * | + | * The ratio of the power of the deterministic part $(|z_0|^2)$ and the stochastic part $(2\sigma^2)$ is $4$. It follows from this: |
| − | :$$2 | + | :$$2 \sigma^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma^2 = 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \frac{1}{\sqrt{10}} \hspace{0.25cm} \underline{ \approx 0.316} \hspace{0.05cm},$$ |
:$$|z_0|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |z_0| = 0.894 | :$$|z_0|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |z_0| = 0.894 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The phase of $z_0 = x_0 + {\rm j} \cdot y_0$ results from the graph. You can see that $y_0 = x_0$ $($center of the cloud in the first quadrant below $45^\circ)$: |
:$$x_0 = y_0 = \frac{|z_0|}{\sqrt{2}} = \frac{0.894}{\sqrt{2}} \hspace{0.25cm} \underline{ \approx 0.632} \hspace{0.05cm}.$$ | :$$x_0 = y_0 = \frac{|z_0|}{\sqrt{2}} = \frac{0.894}{\sqrt{2}} \hspace{0.25cm} \underline{ \approx 0.632} \hspace{0.05cm}.$$ | ||
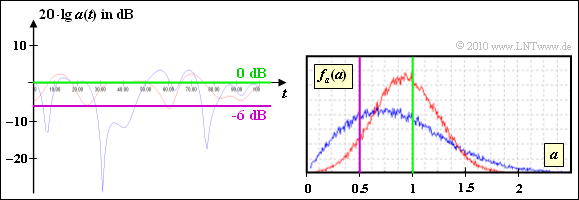
| − | '''(3)''' | + | [[File:P_ID2136__Mob_Z_1_6c.png|right|frame|PDF $f_a(a)$ for Rayleigh and Rice and signal cutout]] |
| − | * | + | '''(3)''' The range $20 \cdot {\rm lg} \, |z(t)| ≤ \, –6 \ \ \rm dB$ is equal to $|z(t)|≤0.5$. |
| − | * | + | *This area is marked by the purple circle in the graph on the first page. |
| + | *You can see from this that <u>statement 1 is correct</u>, because with Rayleigh there are more points within the violet circle. | ||
| − | + | The graph shows the result of a system simulation with the program "Mobile radio channel" from the (former) practical course "Simulation of digital transmission systems". | |
| + | :Both from the signal section as well as from the PDF one can see that the blue curve (Rayleigh) has more parts under the violet curve than the red curve (Rice). | ||
| − | + | ||
| − | + | '''(4)''' Correct is <u>solution 3</u>: | |
| − | + | *For the Rayleigh distribution, the requested probability is | |
| − | '''(4)''' | + | :$${\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a(t) \le 0\,\,{\rm dB}) = {\rm Pr}(a(t) \le 1) = 1 - {\rm e}^{-1} \approx 63\%\,\,\ |
| − | * | ||
| − | :$${\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a(t) \le 0\,\,{\rm dB}) = {\rm Pr}(a(t) \le 1) = | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *From the graph you can see that the probability for the Rice version (with the selected parameters) is about the same as the probability of falling below. |
| − | + | *This result can also be guessed from the complex representation of $z(t)$ on the first page (easier if you already know the result). | |
| − | + | * Among other things, because the center of the Gaussian cloud is still within the green circle. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | * | ||
| − | |||
| − | |||
| − | |||
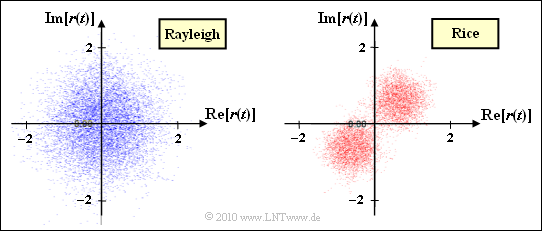
| + | [[File:P_ID2137__Mob_Z_1_6e.png|right|frame|Complex received signal $r(t)$ for Rayleigh and Rice]] | ||
| + | '''(5)''' <u>Solutions 2 and 3</u> are correct: | ||
| + | * With Rice fading, the point cloud of $z(t)$ is in the first quadrant. If you multiply $z(t)$ by $s(t) = ±1$, you get two point clouds in the first and third quadrant. This does not change the PDF $f_a(a)$ of the magnitude. | ||
| + | * Also with Rayleigh fading, the density functions $f_a(a)$ of the magnitudes of $|z(t)|$ and $|r(t)|$ do not show any differences. Since the phase $\phi$ is equally distributed, the final result also has the same point clouds. | ||
| + | *However, if you look at the development of the complex representation of $z(t)$ and $r(t)$ dynamically, there are indeed differences. | ||
| + | *Larger jumps occur in the complex representation of $r(t)$, whenever there are phase jumps by $±180^\circ$ in the transmitted signal $s(t)$, i.e. when changing symbols. | ||
| + | *Thus, ${\it \Phi}_z(f_{\rm D})$ and ${\it \Phi}_r(f_{\rm D})$ are different for Rice fading (the latter is wider) and accordingly the corresponding auto-correlation function. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | + | [[Category:Mobile Communications: Exercises|^1.4 Fading with Direct Path Component^]] | |
| − | [[Category: | ||
Latest revision as of 13:19, 18 January 2023
In this task "Rayleigh fading" and "Rice fading" are to be compared with each other.
The graph shows the complex factor $z(t) = x(t) + {\rm j} \cdot y(t)$ in the complex plane. For the low-pass transmission signal $s(t) = 1$ $($which with respect to a band-pass system corresponds to a cosine oscillation with amplitude $1)$, the low-pass reception signal is $r(t)=z(t)$.
- The upper diagram describes Rayleigh fading, where the component signals $x(t)$ and $y(t)$ are each Gaussian distributed with variance $\sigma^2$. For $a ≥ 0$, the probability density function of the magnitude $a(t) = |z(t)|$ is:
- $$f_a(a) = {a}/{\sigma^2} \cdot {\rm e}^{ -{a^2 }/({2\sigma^2})} \hspace{0.05cm}.$$
- The noncentral second moment ("power") of $z(t)$ is $1$:
- $${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma = {1}/{\sqrt{2}} \approx 0.707 \hspace{0.05cm}.$$
- The lower phase diagram is the result of Rice fading. Here, too, $x(t)$ and $y(t)$ are Gaussian distributed with variance $\sigma^2$, but now with mean value $x_0$ and $y_0$. The PDF for $a ≥ 0$ is
- $$f_a(a) ={a}/{\sigma^2} \cdot {\rm e}^{ -{(a^2+ |z_0|^2) }/({2\sigma^2})}\cdot {\rm I}_0 \left [ {a \cdot |z_0|}/{\sigma^2} \right ]\hspace{0.05cm}.$$
- where ${\rm I}_0$ is the modified Bessel function of the first kind. The power now includes the contribution of the direct component $z_0 = x_0 + {\rm j} \cdot y_0$:
- $${\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$
For the system comparison
- the second moment is assumed to be constant: ${\rm E}\big[|z(t)|^2\big] = 1$,
- the Rice fading is based on the direction shown in the graph,
- let the power be split between the direct path $(|z_0|^2)$ and the scattering paths $(2\sigma^2)$ in the ratio $4:1$ .
For the subtasks (1) to (4), let $s(t) = 1$. For the subtasks (5) and (6), a BPSK signal is assumed . The low-pass signal $s(t)$ thus has a rectangular shape with the possible values $±1$. The duration of each rectangular impulse is $T = 10 \ \rm ms$.
Notes:
- This task belongs to chapter Non-frequency selective fading with direct component.
- The circles drawn in the graph (violet and green) refer to the subtasks (3) and (4).
Questions
Solution
- The first suggestion corresponds to a Rayleigh fading model. With the last setting, we would have
- $$|z(t)| = {\rm j} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \cdot z(t) = {\rm j} \cdot s(t) \hspace{0.05cm}.$$
- If we take into account that we are in the equivalent low-pass range, then a cosine input would produce a negative sinusoidal band-pass signal $r_{\rm BP}(t)$.
- On the other hand, solution 2 applies to all possible signals:
- $$|z(t)| = x_0 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \hspace{0.05cm}.$$
(2) For the given Rayleigh fading, we have $\sigma^2 = 0.5$. For the second moment of the multiplicative factor $z(t)$, this results in:
- $${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.05cm}.$$
The Rice fading should have exactly the same performance. That is, it should apply:
- $$|z_0|^2 + 2 \sigma^2 = 1 \hspace{0.05cm}.$$
Furthermore, it was requested:
- The ratio of the power of the deterministic part $(|z_0|^2)$ and the stochastic part $(2\sigma^2)$ is $4$. It follows from this:
- $$2 \sigma^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma^2 = 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \frac{1}{\sqrt{10}} \hspace{0.25cm} \underline{ \approx 0.316} \hspace{0.05cm},$$
- $$|z_0|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |z_0| = 0.894 \hspace{0.05cm}.$$
- The phase of $z_0 = x_0 + {\rm j} \cdot y_0$ results from the graph. You can see that $y_0 = x_0$ $($center of the cloud in the first quadrant below $45^\circ)$:
- $$x_0 = y_0 = \frac{|z_0|}{\sqrt{2}} = \frac{0.894}{\sqrt{2}} \hspace{0.25cm} \underline{ \approx 0.632} \hspace{0.05cm}.$$
(3) The range $20 \cdot {\rm lg} \, |z(t)| ≤ \, –6 \ \ \rm dB$ is equal to $|z(t)|≤0.5$.
- This area is marked by the purple circle in the graph on the first page.
- You can see from this that statement 1 is correct, because with Rayleigh there are more points within the violet circle.
The graph shows the result of a system simulation with the program "Mobile radio channel" from the (former) practical course "Simulation of digital transmission systems".
- Both from the signal section as well as from the PDF one can see that the blue curve (Rayleigh) has more parts under the violet curve than the red curve (Rice).
(4) Correct is solution 3:
- For the Rayleigh distribution, the requested probability is
- $${\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a(t) \le 0\,\,{\rm dB}) = {\rm Pr}(a(t) \le 1) = 1 - {\rm e}^{-1} \approx 63\%\,\,\ \hspace{0.05cm}.$$
- From the graph you can see that the probability for the Rice version (with the selected parameters) is about the same as the probability of falling below.
- This result can also be guessed from the complex representation of $z(t)$ on the first page (easier if you already know the result).
- Among other things, because the center of the Gaussian cloud is still within the green circle.
(5) Solutions 2 and 3 are correct:
- With Rice fading, the point cloud of $z(t)$ is in the first quadrant. If you multiply $z(t)$ by $s(t) = ±1$, you get two point clouds in the first and third quadrant. This does not change the PDF $f_a(a)$ of the magnitude.
- Also with Rayleigh fading, the density functions $f_a(a)$ of the magnitudes of $|z(t)|$ and $|r(t)|$ do not show any differences. Since the phase $\phi$ is equally distributed, the final result also has the same point clouds.
- However, if you look at the development of the complex representation of $z(t)$ and $r(t)$ dynamically, there are indeed differences.
- Larger jumps occur in the complex representation of $r(t)$, whenever there are phase jumps by $±180^\circ$ in the transmitted signal $s(t)$, i.e. when changing symbols.
- Thus, ${\it \Phi}_z(f_{\rm D})$ and ${\it \Phi}_r(f_{\rm D})$ are different for Rice fading (the latter is wider) and accordingly the corresponding auto-correlation function.