Difference between revisions of "Aufgaben:Exercise 1.2Z: Lognormal Fading Revisited"
From LNTwww
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
|||
| (27 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Distance_Dependent_Attenuation_and_Shading |
}} | }} | ||
| − | [[File:P_ID2123__Mob_Z_1_2.png|right|frame| | + | [[File:P_ID2123__Mob_Z_1_2.png|right|frame|Path loss and lognormal fading]] |
| − | We assume similar conditions as in | + | We assume similar conditions as in [[Aufgaben:Exercise_1.2:_Lognormal_Channel_Model|Exercise 1. 2]] but now we summarize the purely distance-dependent path loss $V_0$ and the mean value $m_{\rm S}$ of the lognormal fading (the index "S" stands for <i>Shadowing</i>): |
| − | $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ | + | :$$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$ |
The total path loss is then given by the equation | The total path loss is then given by the equation | ||
| − | $$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$ | + | :$$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$ |
| − | where $V_2(t)$ describes a ''lognormal | + | where $V_2(t)$ describes a ''lognormal distribution'' with mean value zero: |
| − | $$f_{ | + | :$$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) }\hspace{0.05cm}.$$ |
The path loss model shown in the graphic is suitable for the scenario described here: | The path loss model shown in the graphic is suitable for the scenario described here: | ||
| − | *Multiply the transmitted signal $s(t)$ first with a constant factor $k_1$ and further with a stochastic quantity $z_2(t)$ with the probability density ( | + | *Multiply the transmitted signal $s(t)$ first with a constant factor $k_1$ and further with a stochastic quantity $z_2(t)$ with the probability density function $\rm (PDF)$ $f_{\rm z_2}(z_2)$. |
| − | *The | + | * Then the signal $r(t)$ results at the output, whose power $P_{\rm E}(t)$ is of course also time-dependent due to the stochastic component. |
| − | $$f_{ | + | *The PDF of the lognormally distributed random variable $z_2$ is for $z_2 ≥ 0$: |
| + | :$$f_{z_{\rm 2}}(z_{\rm 2}) = \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}) | ||
| + | /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) | ||
| + | } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.8cm}{\rm with} \hspace{0.8cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | *For $z_2 ≤ 0$ this | + | *For $z_2 ≤ 0$ this PDF is equal to zero. |
| Line 27: | Line 30: | ||
''Notes:'' | ''Notes:'' | ||
| − | * | + | * This exercise belongs to the chapter [[Mobile_Communications/Distance_dependent_attenuation_and_shading|Distance dependent attenuation and shading]]. |
* Use the following parameters: | * Use the following parameters: | ||
| − | $$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$ | + | :$$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$ |
| − | * The probability that a mean-free Gaussian random variable $z$ is greater than its | + | * The probability that a mean-free Gaussian random variable $z$ is greater than its standard deviation $\sigma$, is |
| − | $${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$ | + | :$${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$ |
| − | * Also | + | * Also, ${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$ |
| − | * Again for clarification: $z_2$ is the linear | + | * Again for clarification: $z_2$ is the fading coefficient in linear units, while $V_2$ is the fading coefficient in logarithmic units. |
*The following conversions apply: | *The following conversions apply: | ||
| − | $$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} | + | :$$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} |
| − | V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$ | + | V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$ |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
{How large should the constant $k_1$ be? | {How large should the constant $k_1$ be? | ||
| Line 54: | Line 57: | ||
- The largest possible value is $z_2 = 2$. | - The largest possible value is $z_2 = 2$. | ||
| − | {Calculate the | + | {Calculate the PDF $f_{\rm z2}(z_2)$ for some abscissa values. |
|type="{}"} | |type="{}"} | ||
$f_{\rm z2}(z_2 = 0)\ = \ $ { 0. } | $f_{\rm z2}(z_2 = 0)\ = \ $ { 0. } | ||
| Line 67: | Line 70: | ||
| − | {What statements are valid for the average | + | {What statements are valid for the average received power ${\rm E}\big [P_{\rm E}(t)\big]$? <u>Note:</u> $P_{\rm E}'$ is the power after multiplication by $k_1$ (see diagram). |
|type="[]"} | |type="[]"} | ||
| − | - | + | - ${\rm E}[P_{\rm E}(t)] = P_{\rm E}'$ |
| − | - | + | - ${\rm E}[P_{\rm E}(t)] < P_{\rm E}'$. |
| − | + | + | + ${\rm E}[P_{\rm E}(t)] > P_{\rm E}'$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The constant $k_1$ generates the time-independent path loss $V_1 = 60 \ \rm dB$. From this follows: | + | '''(1)''' The constant $k_1$ generates the time-independent path loss $V_1 = 60 \ \rm dB$. From this follows: |
| − | $$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$ | + | :$$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$ |
| − | '''(2)''' | + | '''(2)''' Only the <u>second statement</u> is correct: |
| − | *For the Gaussian random variable $V_2$ all values between | + | *For the Gaussian random variable $V_2$ all values between $-∞$ and $+∞$ are (theoretically) possible. |
| − | *The transformation $z_2 = 10^{{\it | + | *The transformation $z_2 = 10^{{\it -V_2}\rm /20}$ results in only positive values for the linear random variable $z_2$, <br>namely between 0 $($if $V_2$ is positive and goes to infinity$)$ and $+∞$ $($very large negative values of $V_2)$. |
| − | '''(3)'' The random value $z_2$ can only be positive. Therefore the | + | '''(3)''' The random value $z_2$ can only be positive. Therefore the PDF value $f_{\rm z2}(z_2 = 0)\hspace{0.15cm}\underline{= 0}$. |
| − | * | + | *The PDF–value for the abscissa value $z_2 = 1$ is obtained by inserting it into the given equation: |
| − | :$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | + | :$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}=1) |
| + | /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) | ||
| + | } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)} = | ||
\frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } | \frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } | ||
\hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$ | \hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$ | ||
| − | * | + | *The first portion is equal to the PDF–value $f_{V2}(V_2 = 0)$. |
| − | *$C$ | + | *$C$ considers the magnitude of the derivative of the non-linear characteristic $z_2 = g(V_2)$ for $V_2 = 0 \ \rm dB$ or $z_2 = 1$. |
| − | * | + | *Finally, for $z_2 = 2$: |
:$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot | :$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot | ||
{\rm exp } \left [ - \frac {{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot | {\rm exp } \left [ - \frac {{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot | ||
| Line 101: | Line 106: | ||
| − | '''(4)''' | + | '''(4)''' If you take into account the relationship between $z_2$ and $V_2$, you get |
:$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} | :$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
:$${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842} | :$${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = | + | :$${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The probability that a Gaussian variable is greater than $2 \cdot \sigma$ equals ${\rm Q}(2)$: |
| − | :$${\rm Pr}(z_{\rm 2} > 4) | + | :$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' The <u>statement 3</u> is correct: |
| − | * | + | *The first statement is certainly not correct, since the mean value $m_{\rm S}$ refers to the logarithmic received power $($in $\rm dBm)$. |
| − | * | + | *To clarify whether the second or the third statement is correct, we assume $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ and the following PDF for $V_2$: |
:$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) | :$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) | ||
+ 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$ | + 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$ | ||
| − | * | + | *Half of the time, $P_{\rm E} = 1 \ \rm µ W$, while each of the following has $25\%$ probability:: |
| − | :$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} | + | :$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\,}{\rm µ W}\hspace{0.05cm},$$ |
| − | :$$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} | + | :$$V_{\rm 2}= -10\,\,{\,}{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\,}{\rm µ W}\hspace{0.05cm}.$$ |
| − | * | + | *The mean value is then: |
| − | :$${\rm E}[P_{\rm E}(t)] = | + | :$${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+ 0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *This simple calculation with discrete probabilities instead of a continuous PDF indicates that <u>statement 3</u> is correct. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | *This simple calculation with discrete probabilities instead of a continuous | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 179: | Line 142: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^1.1 Distance-Dependent Attenuation^]] |
Latest revision as of 13:38, 23 March 2021
We assume similar conditions as in Exercise 1. 2 but now we summarize the purely distance-dependent path loss $V_0$ and the mean value $m_{\rm S}$ of the lognormal fading (the index "S" stands for Shadowing):
- $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$
The total path loss is then given by the equation
- $$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$
where $V_2(t)$ describes a lognormal distribution with mean value zero:
- $$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) }\hspace{0.05cm}.$$
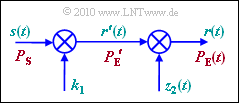
The path loss model shown in the graphic is suitable for the scenario described here:
- Multiply the transmitted signal $s(t)$ first with a constant factor $k_1$ and further with a stochastic quantity $z_2(t)$ with the probability density function $\rm (PDF)$ $f_{\rm z_2}(z_2)$.
- Then the signal $r(t)$ results at the output, whose power $P_{\rm E}(t)$ is of course also time-dependent due to the stochastic component.
- The PDF of the lognormally distributed random variable $z_2$ is for $z_2 ≥ 0$:
- $$f_{z_{\rm 2}}(z_{\rm 2}) = \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}) /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.8cm}{\rm with} \hspace{0.8cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$
- For $z_2 ≤ 0$ this PDF is equal to zero.
Notes:
- This exercise belongs to the chapter Distance dependent attenuation and shading.
- Use the following parameters:
- $$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$
- The probability that a mean-free Gaussian random variable $z$ is greater than its standard deviation $\sigma$, is
- $${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$
- Also, ${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$
- Again for clarification: $z_2$ is the fading coefficient in linear units, while $V_2$ is the fading coefficient in logarithmic units.
- The following conversions apply:
- $$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$
Questions
Solution
(1) The constant $k_1$ generates the time-independent path loss $V_1 = 60 \ \rm dB$. From this follows:
- $$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$
(2) Only the second statement is correct:
- For the Gaussian random variable $V_2$ all values between $-∞$ and $+∞$ are (theoretically) possible.
- The transformation $z_2 = 10^{{\it -V_2}\rm /20}$ results in only positive values for the linear random variable $z_2$,
namely between 0 $($if $V_2$ is positive and goes to infinity$)$ and $+∞$ $($very large negative values of $V_2)$.
(3) The random value $z_2$ can only be positive. Therefore the PDF value $f_{\rm z2}(z_2 = 0)\hspace{0.15cm}\underline{= 0}$.
- The PDF–value for the abscissa value $z_2 = 1$ is obtained by inserting it into the given equation:
- $$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}=1) /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)} = \frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } \hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$
- The first portion is equal to the PDF–value $f_{V2}(V_2 = 0)$.
- $C$ considers the magnitude of the derivative of the non-linear characteristic $z_2 = g(V_2)$ for $V_2 = 0 \ \rm dB$ or $z_2 = 1$.
- Finally, for $z_2 = 2$:
- $$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot {\rm exp } \left [ - \frac {{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot {\rm exp } \left [ - \frac {0.48}{0.952} \right ] \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$
(4) If you take into account the relationship between $z_2$ and $V_2$, you get
- $${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} \hspace{0.05cm},$$
- $${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842} \hspace{0.05cm},$$
- $${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S}) \hspace{0.05cm}.$$
- The probability that a Gaussian variable is greater than $2 \cdot \sigma$ equals ${\rm Q}(2)$:
- $${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} \hspace{0.05cm}.$$
(5) The statement 3 is correct:
- The first statement is certainly not correct, since the mean value $m_{\rm S}$ refers to the logarithmic received power $($in $\rm dBm)$.
- To clarify whether the second or the third statement is correct, we assume $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ and the following PDF for $V_2$:
- $$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) + 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$
- Half of the time, $P_{\rm E} = 1 \ \rm µ W$, while each of the following has $25\%$ probability::
- $$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\,}{\rm µ W}\hspace{0.05cm},$$
- $$V_{\rm 2}= -10\,\,{\,}{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\,}{\rm µ W}\hspace{0.05cm}.$$
- The mean value is then:
- $${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+ 0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} \hspace{0.05cm}.$$
- This simple calculation with discrete probabilities instead of a continuous PDF indicates that statement 3 is correct.