Difference between revisions of "Aufgaben:Exercise 3.2: GSM Data Rates"
m |
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{quiz-Header|Buchseite=Mobile_Communications/Similarities_Between_GSM_and_UMTS | |
| − | {{quiz-Header|Buchseite= | ||
}} | }} | ||
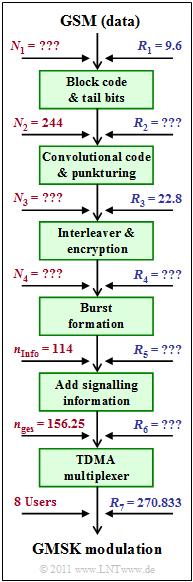
[[File:EN_Mob_A_3_2.png|right|frame|Block diagram of GSM]] | [[File:EN_Mob_A_3_2.png|right|frame|Block diagram of GSM]] | ||
| − | In | + | In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration $T_{\rm R} = 20 \ \rm ms$ of a voice frame as a temporal reference in the following calculations. The input data rate is $R_{1} = 9.6 \ \rm kbit/s$. The number of input bit in each $T_{\rm R}$ frame is $N_{1}$. All parameters labelled "'''???'''" in the graphic should be calculated in the task. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The first blocks shown in the transmission chain are: | |
| − | * | + | *the outer coder (block code including four tail bits) with $N_{2} = 244 \ \rm bit$ per frame $(T_{\rm R} = 20 \ \ \rm ms)$ ⇒ Rate $R_{2}$ is to be determined, |
| − | * | + | *the convolutional coder with the code rate $1/2$, and subsequent puncturing $($waiver of $N_{\rm P} \ \rm bit)$ ⇒ Rate $R_{3} = 22.8 \ \rm kbit/s$, |
| − | + | *interleaving and encryption, both rate-neutral. At the output of this block the rate $R_4$ occurs. | |
| − | + | The further signal processing is basically as follows: | |
| + | *Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm bits)$ to a so called ''Normal Burst''. The rate at the output is $R_{5}$. | ||
| + | *Additionally, further bursts (''Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts'') are added for signalling. The rate after this block is $R_{6}$. | ||
| + | *Finally the TDMA multiplexing equipment follows, so that the total gross data rate of GSM is $R_{\rm tot} = R_{7}$ . | ||
| + | The total gross digital data rate $R_{\rm tot} = 270,833 \ \rm kbit/s$ (for eight users) is assumed to be known. | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The task belongs to the chapter [[Mobile_Communications/Similarities_Between_GSM_and_UMTS|Similarities between GSM and UMTS]]. |
| − | + | *The graphic above summarizes the present description and defines the data rates used. All rates are given in $ \rm kbit/s$. | |
| − | * | + | *$N_{1}, N_{2}, N_{3}$ and $N_{4}$ denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration $T_{\rm R} = 20 \ \rm ms$. |
| − | + | *$N_{\rm tot} = 156.25$ is the number of bits after burst formation, related to the duration $T_{\rm Z}$ of a TDMA time slot. $N_{\rm Info} = 114$ of which are information bits including channel coding. | |
| − | *$N_{1}, N_{2}, N_{3}$ | ||
| − | *$N_{\rm | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many bits are provided by the source in each frame? |
|type="{}"} | |type="{}"} | ||
| − | $N_{1} \ = \ $ { 192 3% } $\ \rm | + | $N_{1} \ = \ $ { 192 3% } $\ \ \rm bit$ |
| − | { | + | {What is the data rate after the outer coder? |
|type="{}"} | |type="{}"} | ||
| − | $R_{2} \ = \ $ { 12.2 3% } $\ \rm kbit/s$ | + | $R_{2} \ = \ $ { 12.2 3% } $\ \ \rm kbit/s$ |
| − | { | + | {How many bits would the convolutional coder deliver alone (without dotting)? |
|type="{}"} | |type="{}"} | ||
| − | $N_{3}\hspace{0.01cm}' \ = \ $ { 488 3% } $\ \rm | + | $N_{3}\hspace{0.01cm}' \ = \ $ { 488 3% } $\ \ \rm bit$ |
| − | { | + | {How many bits does the dotted convolutional coder actually emit? |
|type="{}"} | |type="{}"} | ||
| − | $N_{3} \ = \ $ { 456 3% } $\ \rm | + | $N_{3} \ = \ $ { 456 3% } $\ \ \rm bit$ |
| − | { | + | {What is the data rate after Interleaver and encryption? |
|type="{}"} | |type="{}"} | ||
| − | $R_{4} \ = \ $ { 22.8 3% } $\ \rm kbit/s$ | + | $R_{4} \ = \ $ { 22.8 3% } $\ \ \rm kbit/s$ |
| − | { | + | {How long does a time slot last? |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm Z} \ = \ $ { 576.9 3% } $\ \rm µ s$ | + | $T_{\rm Z} \ = \ $ { 576.9 3% } $\ \ \rm µ s$ |
| − | { | + | {What is the gross data rate for each individual TDMA user? |
|type="{}"} | |type="{}"} | ||
| − | $R_{6} \ = \ $ { 33 | + | $R_{6} \ = \ $ { 33,854 3% } $\ \ \rm kbit/s$ |
| − | { | + | {What gross data rate would be without signaling bits? |
|type="{}"} | |type="{}"} | ||
| − | $R_{5} \ = \ $ { 31.25 3% } $\ \rm kbit/s$ | + | $R_{5} \ = \ $ { 31.25 3% } $\ \ \rm kbit/s$ |
</quiz> | </quiz> | ||
| − | === | + | === Sample Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The following applies: |
| + | :$$N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{= 192 \ \rm bit}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Analogous to subtask '''(1)''' applies: |
| − | :$$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm | + | :$$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$ |
| − | |||
| − | '''(3)''' | + | '''(3)''' The convolutional encoder of rate $1/2$ alone would generate exactly $N_{3}\hspace{0.01cm}' \hspace{0.15cm}\underline{= 488}$ output bits from the $N_{2} = 244$ input bits. |
| − | '''(4)''' | + | '''(4)''' In contrast, $N_{3} \hspace{0.15cm}\underline{= 456}$ follows by the specifed data rate $R_{3} = 22.8 \ \rm kbit/s$. |
| − | * | + | *This means that from $N_{3}' = 488 \ \rm bit$, $N_{\rm P} = 32 \ \rm bit$ can be removed by puncturing. |
| − | '''(5)''' | + | '''(5)''' Both the interleaving and the encryption are "data neutral". Thus the following applies: |
:$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$ | :$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$ | ||
| − | '''(6)''' | + | '''(6)''' The bit duration is $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \rm Mbit/s}) \approx 3.69 \ \rm µ s$. |
| − | *In | + | *In every time slot $T_{\rm Z}$ a burst of $156.25 \ \rm bit$ will be transmitted. |
| − | * | + | *This makes $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$. |
| − | '''(7)''' | + | '''(7)''' GSM has eight time slots, whereby each user is periodically assigned a time slot. |
| − | * | + | *The gross data rate for each user is $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$. |
| − | '''(8)''' | + | '''(8)''' Considering that in the "normal burst" the portion of user data (including channel coding) is $114/156.25$. |
| − | :$$R_5 = \frac{n_{\rm | + | * The rate would be without consideration of the added signaling bits: |
| − | * | + | :$$R_5 = \frac{n_{\rm tot} }{n_{\rm Info} } \cdot R_4 = \frac{156.25}{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$ |
| − | :$$R_5 = \frac{12 }{13 } \cdot 33.854\,{\rm kbit/s} ={ 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$ | + | *The same result can be obtained if you consider that in GSM every thirteenth frame is reserved for "Common Control" (signaling info): |
| − | * | + | :$$R_5 = \frac{12}{13} \cdot 33.854\,{\rm kbit/s} ={ 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$ |
| + | *Thus the percentage of signaling bits is | ||
:$$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$ | :$$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$ | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^3.2 Similarities between GSM and UMTS |
^]] | ^]] | ||
Latest revision as of 13:38, 23 March 2021
In this task, the data transmission with GSM is considered. However, since this system was mainly specified for voice transmission, we usually use the duration $T_{\rm R} = 20 \ \rm ms$ of a voice frame as a temporal reference in the following calculations. The input data rate is $R_{1} = 9.6 \ \rm kbit/s$. The number of input bit in each $T_{\rm R}$ frame is $N_{1}$. All parameters labelled "???" in the graphic should be calculated in the task.
The first blocks shown in the transmission chain are:
- the outer coder (block code including four tail bits) with $N_{2} = 244 \ \rm bit$ per frame $(T_{\rm R} = 20 \ \ \rm ms)$ ⇒ Rate $R_{2}$ is to be determined,
- the convolutional coder with the code rate $1/2$, and subsequent puncturing $($waiver of $N_{\rm P} \ \rm bit)$ ⇒ Rate $R_{3} = 22.8 \ \rm kbit/s$,
- interleaving and encryption, both rate-neutral. At the output of this block the rate $R_4$ occurs.
The further signal processing is basically as follows:
- Each $114$ (coded, scrambled, encrypted) data bits are combined together with $34$ control bits (for training sequence, tail bits, guard period) and a pause $($Duration: $8.25 \ \ \rm bits)$ to a so called Normal Burst. The rate at the output is $R_{5}$.
- Additionally, further bursts (Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts) are added for signalling. The rate after this block is $R_{6}$.
- Finally the TDMA multiplexing equipment follows, so that the total gross data rate of GSM is $R_{\rm tot} = R_{7}$ .
The total gross digital data rate $R_{\rm tot} = 270,833 \ \rm kbit/s$ (for eight users) is assumed to be known.
Notes:
- The task belongs to the chapter Similarities between GSM and UMTS.
- The graphic above summarizes the present description and defines the data rates used. All rates are given in $ \rm kbit/s$.
- $N_{1}, N_{2}, N_{3}$ and $N_{4}$ denote the respective number of bits at the corresponding points of the above block diagram within a time frame of duration $T_{\rm R} = 20 \ \rm ms$.
- $N_{\rm tot} = 156.25$ is the number of bits after burst formation, related to the duration $T_{\rm Z}$ of a TDMA time slot. $N_{\rm Info} = 114$ of which are information bits including channel coding.
Questionnaire
Sample Solution
(1) The following applies:
- $$N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{= 192 \ \rm bit}.$$
(2) Analogous to subtask (1) applies:
- $$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$
(3) The convolutional encoder of rate $1/2$ alone would generate exactly $N_{3}\hspace{0.01cm}' \hspace{0.15cm}\underline{= 488}$ output bits from the $N_{2} = 244$ input bits.
(4) In contrast, $N_{3} \hspace{0.15cm}\underline{= 456}$ follows by the specifed data rate $R_{3} = 22.8 \ \rm kbit/s$.
- This means that from $N_{3}' = 488 \ \rm bit$, $N_{\rm P} = 32 \ \rm bit$ can be removed by puncturing.
(5) Both the interleaving and the encryption are "data neutral". Thus the following applies:
- $$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$
(6) The bit duration is $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \rm Mbit/s}) \approx 3.69 \ \rm µ s$.
- In every time slot $T_{\rm Z}$ a burst of $156.25 \ \rm bit$ will be transmitted.
- This makes $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$.
(7) GSM has eight time slots, whereby each user is periodically assigned a time slot.
- The gross data rate for each user is $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$.
(8) Considering that in the "normal burst" the portion of user data (including channel coding) is $114/156.25$.
- The rate would be without consideration of the added signaling bits:
- $$R_5 = \frac{n_{\rm tot} }{n_{\rm Info} } \cdot R_4 = \frac{156.25}{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$
- The same result can be obtained if you consider that in GSM every thirteenth frame is reserved for "Common Control" (signaling info):
- $$R_5 = \frac{12}{13} \cdot 33.854\,{\rm kbit/s} ={ 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$
- Thus the percentage of signaling bits is
- $$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$