Difference between revisions of "Aufgaben:Exercise 4.3: Subcarrier Mapping"

From LNTwww
 
(11 intermediate revisions by 3 users not shown)
Line 1: Line 1:
  
−
{{quiz-Header|Buchseite=Mobile Kommunikation/Die Anwendung von OFDMA und SC-FDMA in LTE
+
{{quiz-Header|Buchseite=Mobile_Communications/The_Application_of_OFDMA_and_SC-FDMA_in_LTE
  
 
}}
 
}}
  
  
−
[[File:EN_Mob_A_4_3.png|right|frame|Two SC-FDMA&ndash [arrangements]]
+
[[File:EN_Mob_A_4_3.png|right|frame|Two SC–FDMA arrangements]]
−
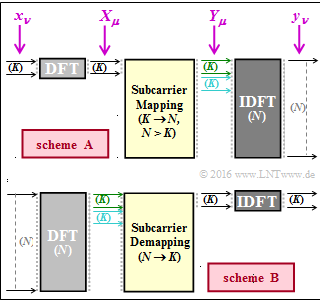
The diagram shows two transmission schemes that play a role in connection with  ''Long Term Evolution''  (LTE). These block diagrams are referred here neutrally as "arrangement  $\rm A$” or "arrangement  $\rm B$".
+
The diagram shows two transmission schemes that play a role in connection with  Long Term Evolution  $\rm (LTE)$.  These block diagrams are referred here neutrally as  "arrangement  $\rm A$"  or  "arrangement  $\rm B$".
 
* The light grey blocks represent the transition from the time to the frequency domain.
 
* The light grey blocks represent the transition from the time to the frequency domain.
 
* The dark grey blocks represent the transition from the frequency to the time domain.
 
* The dark grey blocks represent the transition from the frequency to the time domain.
Line 13: Line 13:
 
We refer here to the following links:
 
We refer here to the following links:
  
−
* [[Signal_Representation/Diskrete_Fouriertransformation_(DFT)#Von_der_kontinuierlichen_zur_diskreten_Fouriertransformation|Diskrete Fouriertransformation]]   ⇒   „DFT” ,
+
* [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Von_der_kontinuierlichen_zur_diskreten_Fouriertransformation|Discrete Fourier Transform]]   ⇒   $\rm DFT$,
  
−
* [[Signal_Representation/Diskrete_Fouriertransformation_(DFT)#Inverse_Diskrete_Fouriertransformation|Inverse Diskrete Fouriertransformation]]   ⇒   „IDFT” .
+
* [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Inverse_Discrete_Fourier_Transform|Inverse Discrete Fourier Transform]]   ⇒   $\rm IDFT$.
  
  
−
Für die Stützstellenanzahl von DFT und IDFT werden mit  $K = 12$  und  $N = 1024$  realistische Zahlenwerte angenommen.
+
For the number of interpolation points of DFT and IDFT, realistic numerical values of  $K = 12$  and  $N = 1024$  are assumed.
−
*Der Wert  $K = 12$  ergibt sich aus der Tatsache, dass durch das  ''Subcarrier–Mapping''  die Symbole auf eine gewisse Bandbreite „gemappt” werden. Der kleinste adressierbare Block ist bei LTE  $180 \ \rm kHz$. Mit dem Unterträgerabstand von  $15 \ \rm kHz$ ergibt sich  $K = 12$.
+
*The value  $K = 12$  results from the fact that the symbols are "mapped" to a certain bandwidth by the  "subcarrier mapping".  The smallest addressable block for LTE is  $180 \ \rm kHz$.  With  the subcarrier spacing of  $15 \ \rm kHz$   the value  $K = 12$  results.
−
*Mit der Stützstellenanzahl  $N$  der IDFT $($bei Anordnung   $\rm A)$  können somit bis zu  $J = N/K$  Nutzer gleichzeitig bedient werden. Für das  ''Subcarrier–Mapping''  gibt es mit DFDMA, IFDMA und LFDMA drei verschiedene Ansätze.
+
*With the number  $N$  of interpolation points of the IDFT $($with arrangement $\rm A)$ , up to  $J = N/K$  users can thus be served simultaneously.  For subcarrier mapping, there are three different approaches with DFDMA, IFDMA and LFDMA.
−
*Die beiden ersten Nutzer sind in der Grafik grün bzw. türkis eingezeichnet. In der Teilaufgabe '''(5)''' sollen Sie entscheiden, ob die Skizze für DFDMA, IFDMA oder LFDMA gilt.
+
*The first two users are shown in green and turquoise in the diagram.  In subtask  '''(5)'''  you are to decide whether the sketch applies to DFDMA, IFDMA or LFDMA.
  
  
Line 29: Line 29:
  
  
−
''Hinweis:''  
+
''Note:''  
−
*Die Aufgabe gehört zum Kapitel  [[Mobile_Communications/Die_Anwendung_von_OFDMA_und_SC-FDMA_in_LTE|Anwendung von OFDMA und SC-FDMA in LTE]].
+
*The task belongs to the chapter  [[Mobile_Communications/The_Application_of_OFDMA_and_SC-FDMA_in_LTE|The Application of OFDMA and SC-FDMA in LTE]].
  
  
−
===Fragebogen===
+
===Questions===
  
 
<quiz display=simple>
 
<quiz display=simple>
  
−
{Wofür gelten die skizzierten Anordnungen auf der Angabenseite?
+
{What do the outlined arrangements in the information section apply to?
 
|type="()"}
 
|type="()"}
−
- Für den LTE–Downlink,
+
- For the LTE downlink,
−
+ für den LTE–Uplink.
+
+ for the LTE uplink.
  
−
{Welche Einheiten sind auf der Angabenseite dargestellt?
+
{Which units are shown in the information section?
 
|type="[]"}
 
|type="[]"}
−
+ Anordnung &nbsp;$\rm A$&nbsp; zeigt den Sender des LTE–Uplinks.
+
+ Arrangement &nbsp;$\rm A$&nbsp; shows the transmitter of the LTE uplink.
−
+ Anordnung &nbsp;$\rm B$&nbsp; zeigt den Empfänger des LTE–Uplinks.
+
+ Arrangement &nbsp;$\rm B$&nbsp; shows the receiver of the LTE uplink..
−
- Beide Modelle gelten für Sender und Empfänger gleichermaßen.
+
- Both models apply equally to the transmitter and receiver.
  
−
{Welche nicht eingezeichneten Blöcke sind noch erforderlich?
+
{Which blocks not shown are still required?
 
|type="[]"}
 
|type="[]"}
−
+ Vor Anordnung &nbsp;$\rm A$&nbsp; benötigt man einen Seriell–Parallel–Wandler.
+
+ Before arrangement &nbsp;$\rm A$&nbsp; you need a serial-parallel converter.
−
+ Nach Anordnung &nbsp;$\rm B$&nbsp; benötigt man einen Parallel–Seriell–Wandler.
+
+ After arrangement &nbsp;$\rm B$&nbsp; you need a parallel-serial converter.
  
  
−
{Wie viele Nutzer&nbsp; $(J)$&nbsp; kann man mit&nbsp; $K = 12$&nbsp; und&nbsp; $N = 1024$&nbsp; gleichzeitig bedienen?
+
{How many users&nbsp; $(J)$&nbsp; can be served simultaneously with&nbsp; $K = 12$&nbsp; and&nbsp; $N = 1024$&nbsp;?
 
|type="{}"}
 
|type="{}"}
 
$J \ = \ $ { 85 3% }
 
$J \ = \ $ { 85 3% }
  
−
{Welches Mapping liegt der Grafik auf der Angabenseite zugrunde?
+
{Which mapping is the graphic in the information section based on?
 
|type="()"}
 
|type="()"}
 
- Distributed Mapping&nbsp; (DFDMA),
 
- Distributed Mapping&nbsp; (DFDMA),
Line 64: Line 64:
 
+ Localized Mapping&nbsp; (LFDMA).
 
+ Localized Mapping&nbsp; (LFDMA).
  
−
{Welche DFT (IDFT) lassen sich als FFT (IFFT) realisieren?
+
{Which DFT (IDFT) can be realised as FFT (IFFT)?
 
|type="[]"}
 
|type="[]"}
−
- Die DFT im linken Bereich von Anordnung &nbsp;$\rm A$.
+
- The DFT in the left area of arrangement &nbsp;$\rm A$.
−
+ Die IDFT im rechten Bereich von Anordnung &nbsp;$\rm A$.
+
+ The IDFT in the right-hand area of arrangement &nbsp;$\rm A$.
−
+ Die DFT im linken Bereich von Anordnung &nbsp;$\rm B$.
+
+ The DFT in the left-hand area of arrangement &nbsp;$\rm B$.
−
- Die IDFT im rechten Bereich von Anordnung &nbsp;$\rm B$.
+
- The IDFT in the right-hand area of arrangement &nbsp;$\rm B$.
  
 
</quiz>
 
</quiz>
  
−
===Musterlösung===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
  
−
'''(1)'''&nbsp; Richtig ist der <u>Lösungsvorschlag 2</u>:
+
'''(1)'''&nbsp; <u>Proposed solution 2</u> is correct:
−
*Beide Anordnungen zeigen ''Single Carrier Frequency Division Multiple Access'' (SC–FDMA), erkennbar an den DFT– und IDFT–Blöcken.  
+
*Both arrangements show "Single Carrier Frequency Division Multiple Access"&nbsp; $\text{(SC–FDMA)}$, recognisable by the DFT and IDFT blocks.  
−
*Der Vorteil gegenüber ''Orthogonal Frequency Division Multiple–Access'' (OFDMA) ist das günstigere ''Peak–to–Average Power–Ratio'' (PAPR).  
+
*The advantage over "Orthogonal Frequency Division Multiple–Access"&nbsp; $\text{(OFDMA)}$&nbsp; is the more favourable Peak–to–Average Power–Ratio&nbsp; $\text{(PAPR)}$.  
−
*Ein großes PAPR führt dazu, dass man die Verstärker unterhalb der Sättigungsgrenze und damit bei schlechterem Wirkungsgrad betreiben muss, um zu starke Signalverzerrungen zu verhindern.  
+
*A large PAPR means that the amplifiers must be operated below the saturation limit and thus at poorer efficiency in order to prevent excessive signal distortion.
−
*Ein niedrigeres PAPR bedeutet gleichzeitig eine längere Batterielaufzeit, ein für Smartphones äußerst wichtiges Kriterium.  
+
*A lower PAPR also means longer battery life, an extremely important criterion for smartphones.
−
*Deshalb wird SC–FDMA im LTE–Uplink eingesetzt. Für den Downlink ist der hier genannte Aspekt weniger bedeutend.
+
*This is why SC-FDMA is used in the LTE uplink.&nbsp; For the downlink, the aspect mentioned here is less significant.
  
  
  
−
'''(2)'''&nbsp;  Richtig sind die <u>Lösungsvorschläge 1 und 2</u>:
+
'''(2)'''&nbsp;  <u>Proposed solutions 1 and 2 </u>are correct:
−
*Während bei OFDMA die zu übertragenden Datensymbole direkt die verschiedenen Unterträger erzeugen, wird bei SC–FDMA ein Block von Datensymbolen mittels DFT zuerst in den Frequenzbereich transformiert.  
+
*While in OFDMA the data symbols to be transmitted directly generate the various subcarriers, in SC-FDMA a block of data symbols is first transformed into the frequency domain using DFT.  
−
*Um mehrere Nutzer übertragen zu können, muss $N > K$ gelten. Ein Eingangsblock eines Nutzers besteht somit aus $K$ Bit. Damit ist offensichtlich, dass die Anordnung &nbsp;$\rm A$&nbsp; für den Sender gilt.  
+
*To be able to transmit multiple users, $N > K$ must apply.&nbsp; An input block of a user thus consists of $K$ bits.&nbsp; It is thus obvious that arrangement&nbsp;$\rm A$&nbsp; applies to the transmitter.  
−
*Die Anordnung &nbsp;$\rm B$&nbsp; beschreibt dagegen den Empfänger des LTE–Uplinks und nicht den Sender.
+
*Arrangement &nbsp;$\rm B$,&nbsp; on the other hand, describes the receiver of the LTE uplink and not the transmitter.
  
  
 +
'''(3)'''&nbsp;  <u>Both statements</u> are correct:
 +
*The measures are necessary to be able to process a continuous bit stream at the transmitter,
 +
*or to ensure a continuous bit stream at the receiver as well.
  
−
'''(3)'''&nbsp;  <u>Beide Aussagen</u> sind zutreffend:
 
−
*Die Maßnahmen sind erforderlich,  um einen kontinuierlichen Bitstrom am Sender verarbeiten zu können bzw. auch beim Empfänger einen kontinuierlichen Bitstrom zu gewährleisten.
 
  
 +
'''(4)'''&nbsp; The DFT also generates&nbsp; $K$&nbsp; spectral values from&nbsp; $K$&nbsp; input values.
 +
*The subcarrier mapping does not change anything.
 +
*Further users also occupy&nbsp; $K$&nbsp; (bits) of the total of&nbsp; $N$&nbsp; (bits).
 +
*Thus&nbsp; $J = N/K = 1024/12 = 85.333$  &nbsp; &rArr; &nbsp;  $J \ \underline{= 85}$&nbsp; users can be supplied.
  
  
−
'''(4)'''&nbsp; Die DFT erzeugt aus $K$ Eingangswerten ebenfalls $K$ Spektralwerte.
+
'''(5)'''&nbsp; <u>Proposed solution 3</u> is correct:
−
*Durch das ''Subcarrier–Mapping'' ändert sich dadurch nichts.  
+
*The graph conforms to the current 3gpp specification, which provides for "Localized Mapping".
−
*Durch weitere Nutzer werden ebenfalls jeweils $K$ (Bit)  der insgesamt $N$  (Bit) belegt.
+
*Here, the&nbsp; $K$&nbsp; modulation symbols are assigned to adjacent subcarriers.
−
*Damit können $J = N/K = 1024/12 = 85.333$  &nbsp; &rArr; &nbsp; $J \ \underline{= 85}$ Nutzer versorgt werden.
 
  
  
  
−
'''(5)'''&nbsp; Richtig ist der <u>Lösungsvorschlag 3</u>:
+
'''(6)'''&nbsp; <u>Solutions 2 and 3</u> are correct:
−
*Die Grafik entspricht der derzeitigen 3gpp–Spezifikation, die ''Localized Mapping'' vorsieht.
+
*The realisation of DFT or IDFT as an (inverse) "Fast Fourier Transform" is only possible if the number of interpolation points is a power of two.
−
*Hierbei werden die $K$ Modulationssymbole benachbarten Unterträgern zugeordnet.
+
*For example, for&nbsp; $N = 1024$, but not for&nbsp; $K = 12$.
−
 
 
−
 
 
−
 
 
−
'''(6)'''&nbsp; Richtig sind die <u>Lösungsvorschläge 2 und 3</u>:
 
−
*Die Realisierung von DFT bzw. IDFT als (inverse) ''Fast Fourier Transform'' ist nur möglich, wenn die Stützstellenzahl eine Zweierpotenz ist.  
 
−
*Also zum Beispiel für $N = 1024$, nicht aber für $K = 12$.
 
  
 
{{ML-Fuß}}
 
{{ML-Fuß}}
Line 118: Line 116:
  
  
−
[[Category:Exercises for Mobile Communications|^4.3 Use of OFDMA and SC-FDMA
+
[[Category:Mobile Communications: Exercises|^4.3 Use of OFDMA and SC-FDMA
  
 
^]]
 
^]]

Latest revision as of 13:43, 17 November 2022


Two SC–FDMA arrangements

The diagram shows two transmission schemes that play a role in connection with  Long Term Evolution  $\rm (LTE)$.  These block diagrams are referred here neutrally as  "arrangement  $\rm A$"  or  "arrangement  $\rm B$".

  • The light grey blocks represent the transition from the time to the frequency domain.
  • The dark grey blocks represent the transition from the frequency to the time domain.


We refer here to the following links:


For the number of interpolation points of DFT and IDFT, realistic numerical values of  $K = 12$  and  $N = 1024$  are assumed.

  • The value  $K = 12$  results from the fact that the symbols are "mapped" to a certain bandwidth by the  "subcarrier mapping".  The smallest addressable block for LTE is  $180 \ \rm kHz$.  With  the subcarrier spacing of  $15 \ \rm kHz$   the value  $K = 12$  results.
  • With the number  $N$  of interpolation points of the IDFT $($with arrangement $\rm A)$ , up to  $J = N/K$  users can thus be served simultaneously.  For subcarrier mapping, there are three different approaches with DFDMA, IFDMA and LFDMA.
  • The first two users are shown in green and turquoise in the diagram.  In subtask  (5)  you are to decide whether the sketch applies to DFDMA, IFDMA or LFDMA.




Note:


Questions

1

What do the outlined arrangements in the information section apply to?

For the LTE downlink,
for the LTE uplink.

2

Which units are shown in the information section?

Arrangement  $\rm A$  shows the transmitter of the LTE uplink.
Arrangement  $\rm B$  shows the receiver of the LTE uplink..
Both models apply equally to the transmitter and receiver.

3

Which blocks not shown are still required?

Before arrangement  $\rm A$  you need a serial-parallel converter.
After arrangement  $\rm B$  you need a parallel-serial converter.

4

How many users  $(J)$  can be served simultaneously with  $K = 12$  and  $N = 1024$ ?

$J \ = \ $

5

Which mapping is the graphic in the information section based on?

Distributed Mapping  (DFDMA),
Interleaved Mapping  (IFDMA),
Localized Mapping  (LFDMA).

6

Which DFT (IDFT) can be realised as FFT (IFFT)?

The DFT in the left area of arrangement  $\rm A$.
The IDFT in the right-hand area of arrangement  $\rm A$.
The DFT in the left-hand area of arrangement  $\rm B$.
The IDFT in the right-hand area of arrangement  $\rm B$.


Solution

Solution

(1)  Proposed solution 2 is correct:

  • Both arrangements show "Single Carrier Frequency Division Multiple Access"  $\text{(SC–FDMA)}$, recognisable by the DFT and IDFT blocks.
  • The advantage over "Orthogonal Frequency Division Multiple–Access"  $\text{(OFDMA)}$  is the more favourable Peak–to–Average Power–Ratio  $\text{(PAPR)}$.
  • A large PAPR means that the amplifiers must be operated below the saturation limit and thus at poorer efficiency in order to prevent excessive signal distortion.
  • A lower PAPR also means longer battery life, an extremely important criterion for smartphones.
  • This is why SC-FDMA is used in the LTE uplink.  For the downlink, the aspect mentioned here is less significant.


(2)  Proposed solutions 1 and 2 are correct:

  • While in OFDMA the data symbols to be transmitted directly generate the various subcarriers, in SC-FDMA a block of data symbols is first transformed into the frequency domain using DFT.
  • To be able to transmit multiple users, $N > K$ must apply.  An input block of a user thus consists of $K$ bits.  It is thus obvious that arrangement $\rm A$  applies to the transmitter.
  • Arrangement  $\rm B$,  on the other hand, describes the receiver of the LTE uplink and not the transmitter.


(3)  Both statements are correct:

  • The measures are necessary to be able to process a continuous bit stream at the transmitter,
  • or to ensure a continuous bit stream at the receiver as well.


(4)  The DFT also generates  $K$  spectral values from  $K$  input values.

  • The subcarrier mapping does not change anything.
  • Further users also occupy  $K$  (bits) of the total of  $N$  (bits).
  • Thus  $J = N/K = 1024/12 = 85.333$   ⇒   $J \ \underline{= 85}$  users can be supplied.


(5)  Proposed solution 3 is correct:

  • The graph conforms to the current 3gpp specification, which provides for "Localized Mapping".
  • Here, the  $K$  modulation symbols are assigned to adjacent subcarriers.


(6)  Solutions 2 and 3 are correct:

  • The realisation of DFT or IDFT as an (inverse) "Fast Fourier Transform" is only possible if the number of interpolation points is a power of two.
  • For example, for  $N = 1024$, but not for  $K = 12$.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_4.3:_Subcarrier_Mapping&oldid=50233"
  • Powered by MediaWiki