Difference between revisions of "Aufgaben:Exercise 1.2: Lognormal Channel Model"
From LNTwww
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Distance_Dependent_Attenuation_and_Shading |
}} | }} | ||
| Line 37: | Line 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Would $P_{\rm E}$ be sufficient | + | {Would $P_{\rm E}$ be sufficient if the loss $V_S$ due to shadowing is not present? |
|type="()"} | |type="()"} | ||
+ Yes, | + Yes, | ||
| Line 55: | Line 55: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' The correct answer is <u>YES</u>: | '''(1)''' The correct answer is <u>YES</u>: | ||
| Line 77: | Line 77: | ||
'''(3)''' The received power is too low $($less than $–80 \ \rm dBm)$ if the power loss due to the lognormal–term is $40 \ \rm dB$ or more. | '''(3)''' The received power is too low $($less than $–80 \ \rm dBm)$ if the power loss due to the lognormal–term is $40 \ \rm dB$ or more. | ||
| − | [[File:EN_Mob_A_1_2c.png|right|frame| | + | [[File:EN_Mob_A_1_2c.png|right|frame|Loss due to lognormal fading]] |
*The distance-dependent path loss $V_{\rm S}$ must therefore not be greater than $20 \ \rm dB$. | *The distance-dependent path loss $V_{\rm S}$ must therefore not be greater than $20 \ \rm dB$. | ||
| Line 105: | Line 105: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^1.1 Distance-Dependent Attenuation^]] |
Latest revision as of 15:58, 2 July 2021
We consider a mobile radio cell in an urban area and a vehicle that is approximately at a fixed distance $d_0$ from the base station. For example, it moves on an arc around the base station.
Thus the total path loss can be described by the following equation:
- $$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$
- $V_0$ takes into account the distance-dependent path loss which is assumed to be constant: $V_0 = 80 \ \rm dB$ .
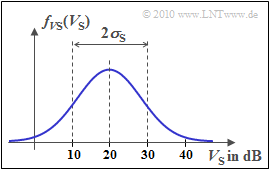
- The loss $V_{\rm S}$ is due to shadowing caused by the lognormal distribution with the probability density function (PDF)
- $$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) },$$
- see diagram. The following numerical values apply:
- $$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.25cm}{\rm or }\hspace{0.25cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (subtask\hspace{0.15cm} 2)}\hspace{0.05cm}.$$
Also make the following simple assumptions:
- The transmit power is $P_{\rm S} = 10 \ \rm W$ $\text{(or } 40 \ \rm dBm$).
- The received power should be at least $P_{\rm E} = 10 \ \rm pW$ $\text{(or } -80 \ \rm dBm$)
Notes:
- This task belongs to the chapter Distance dependent attenuation and shading.
- You can use the following (rough) approximations for the complementary Gaussian error integral:
- $${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$
- Or use the interaction module Complementary Gaussian Error Functions provided by $\rm LNTwww$.
Questions
Solution
(1) The correct answer is YES:
- From the $\rm dB$–value $V_0 = 80 \ \rm dB$ follows the absolute (linear) value $K_0 = 10^8$. Thus the received power is
- $$P_{\rm E} = P_{\rm S}/K_0 = 10 \ {\rm W}/10^8 = 100 \ {\rm nW} > 10 \ \ \rm pW.$$
- You can also solve this problem directly with the logarithmic quantities:
- $$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}{1\,\,{\rm mW}} = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm S}}{1\,\,{\rm mW}} - V_0 = 40\,{\rm dBm} -80\,\,{\rm dB} = -40\,\,{\rm dBm} \hspace{0.05cm}.$$
- Only the limit value $-80 \ \rm dBm$ is required.
(2) Lognormal fading with $\sigma_{\rm S} = 0 \ \rm dB$ is equivalent to a constant received power $P_{\rm E}$.
- Compared to the subtask (1) this is $m_{\rm S} = 20 \ \ \rm dB$ smaller ⇒ $P_{\rm E} = \ –60 \ \ \rm dBm$.
- But it is still greater than the specified limit value $(-80 \ \rm dBm)$.
- It follows: The system is (almost) 100% functional. "Almost" because with a Gaussian random quantity there is always a (small) residual uncertainty.
(3) The received power is too low $($less than $–80 \ \rm dBm)$ if the power loss due to the lognormal–term is $40 \ \rm dB$ or more.
- The distance-dependent path loss $V_{\rm S}$ must therefore not be greater than $20 \ \rm dB$.
- So it follows:
- $${\rm Pr}({\rm "System\hspace{0.15cm}does\hspace{0.15cm}not\hspace{0.15cm}work"})= {\rm Q}\left ( \frac{20\,\,{\rm dB}}{\sigma_{\rm S} = 10\,{\rm dB}}\right ) = {\rm Q}(2) \approx 0.02$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}({\rm "System\hspace{0.15cm}works"})= 1- 0.02 \hspace{0.15cm} \underline{\approx 98\,\%}\hspace{0.05cm}.$$
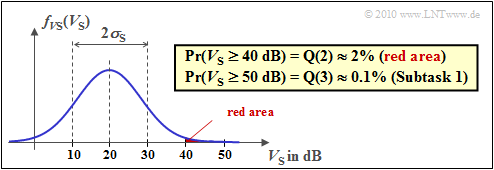
The graphic illustrates the result.
- The probability density $f_{\rm VS}(V_{\rm S})$ of the path loss due to shadowing (Longnormal Fading) is shown here.
- The probability that the system will fail is marked in red.
(4) From the availability probability $99.9 \%$ follows the failure probability $10^{\rm -3} \approx \ {\rm Q}(3)$.
- If the distance-dependent path loss $V_0$ is reduced by $10 \ \ \rm dB$ to $\underline {70 \ \rm dB}$, a failure will only occur when $V_{\rm S} ≥ 50 \ \ \rm dB$.
- This would achieve exactly the required reliability, as the following calculation shows:
- $${\rm Pr}({\rm "System\hspace{0.15cm} does\hspace{0.15cm} not\hspace{0.15cm} work\hspace{0.15cm}"})= {\rm Q}\left ( \frac{120-70-20}{10}\right ) = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.$$