Difference between revisions of "Aufgaben:Exercise 1.5: Reconstruction of the Jakes Spectrum"
m (Text replacement - "power spectral density" to "power-spectral density") |
|||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process}} |
[[File:P_ID2124__Mob_A_1_5.png|right|frame|Considered Jakes spectrum]] | [[File:P_ID2124__Mob_A_1_5.png|right|frame|Considered Jakes spectrum]] | ||
| − | In a mobile radio system, the [[Mobile_Communications/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Doppler effect]] is also noticeable in the power density | + | In a mobile radio system, the [[Mobile_Communications/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Doppler effect]] is also noticeable in the power-spectral density of the Doppler frequency $f_{\rm D}$. |
| − | This results in the so-called [[Mobile_Communications/ | + | This results in the so-called [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#ACF_and_PDS_with_Rayleigh.E2.80.93Fading|Jakes spectrum]], which is shown in the graph for the maximum Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$. ${\it \Phi}_z(f_{\rm D})$ has only portions within the range $± f_{\rm D, \ max}$, where |
| − | :$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0. | + | :$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.1cm} max})^2} } |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | What is expressed in the frequency domain by the power spectral density (PSD) is described in the time domain by the | + | What is expressed in the frequency domain by the power-spectral density $\rm (PSD)$ is described in the time domain by the auto-correlation function $\rm (ACF)$. The ACF is the ${\it \Phi}_z(f_{\rm D})$ by the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_Second_Fourier_Integral|inverse Fourier transform]] of the PDS. |
With the [[Applets:Bessel_Functions_of_the_First_Kind|Bessel function]] of the first kind and zero order $({\rm J}_0)$ you get | With the [[Applets:Bessel_Functions_of_the_First_Kind|Bessel function]] of the first kind and zero order $({\rm J}_0)$ you get | ||
| − | :$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0. | + | :$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ |
| − | To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the [[Mobile_Communications/ | + | To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the [[Mobile_Communications/Probability_Density_of_Rayleigh_Fading|Rayleigh channel model]], each with the frequency response $H_{\rm DF}(f_{\rm D})$. |
The dimensioning of these filters is part of this task. | The dimensioning of these filters is part of this task. | ||
*We restrict ourselves here to the branch for generating the real part $x(t)$. The ratios derived here are also valid for the imaginary part $y(t)$. | *We restrict ourselves here to the branch for generating the real part $x(t)$. The ratios derived here are also valid for the imaginary part $y(t)$. | ||
| − | *At the input of the left digital filter of the [[Mobile_Communications/ | + | *At the input of the left digital filter of the [[Mobile_Communications/Probability_Density_of_Rayleigh_Fading#Modeling_of_non-frequency_selective_fading|Rayleigh channel model]] , there is white Gaussian noise $n(t)$ with variance $\sigma^2 = 0.5$. |
*The real component is then obtained from the following convolution | *The real component is then obtained from the following convolution | ||
:$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | :$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | ||
| Line 25: | Line 25: | ||
''Notes:'' | ''Notes:'' | ||
| − | * This task belongs to the topic of [[Mobile_Communications/ | + | * This task belongs to the topic of [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process|Statistical bindings within the Rayleigh process]]. |
| − | * The digital filter is treated in detail in chapter [[Theory_of_Stochastic_Signals/Digitale_Filter| | + | * The digital filter is treated in detail in chapter [[Theory_of_Stochastic_Signals/Digitale_Filter|Digital Filter]] of the book "Stochastic Signal Theory". |
| Line 36: | Line 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the value of the Jakes | + | {What is the value of the Jakes spectrum of the real part at the Doppler frequency $f_{\rm D} = 0$? |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_x(f_{\rm D} = 0)\ = \ $ { 1.59 } $\ \cdot 10^{\rm –3} \ | + | ${\it \Phi}_x(f_{\rm D} = 0)\ = \ $ { 1.59 } $\ \cdot 10^{\rm –3} \ {\rm Hz}^{-1}$ |
{Which dimensioning is correct, where $K$ is an appropriately chosen constant? | {Which dimensioning is correct, where $K$ is an appropriately chosen constant? | ||
| Line 51: | Line 51: | ||
+ The integral over $|H_{\rm DF}(f_{\rm D})|^2$ must be $1$ . | + The integral over $|H_{\rm DF}(f_{\rm D})|^2$ must be $1$ . | ||
| − | {Is $H_{\rm DF}(f)$ unambiguously defined by the two conditions according to '''(2)'' and '''(3)'''? | + | {Is $H_{\rm DF}(f)$ unambiguously defined by the two conditions according to '''(2)''' and '''(3)'''? |
|type="()"} | |type="()"} | ||
- Yes. | - Yes. | ||
| Line 57: | Line 57: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The Jakes spectrum of the real part is half the resulting spectrum ${\it \Phi}_z(f)$: | + | '''(1)''' The Jakes spectrum of the real part is half the resulting spectrum ${\it \Phi}_z(f)$: |
:$${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = | :$${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = | ||
\frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} | \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} | ||
| Line 66: | Line 66: | ||
'''(2)''' <u>Solution 2</u> is correct: | '''(2)''' <u>Solution 2</u> is correct: | ||
| − | *The input signal $n(t)$ has a white (constant) | + | *The input signal $n(t)$ has a white (constant) PDS ${\it \Phi}_n(f_{\rm D})$. |
| − | *The | + | *The PDS at the output is then |
| − | $${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 | + | :$${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
'''(3)''' <u>Solution 3</u> is correct. | '''(3)''' <u>Solution 3</u> is correct. | ||
| − | *Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$. | + | *Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$. |
'''(4)''' <u>No</u>: | '''(4)''' <u>No</u>: | ||
| − | *The two conditions after subtasks (2) and (3) only refer to the magnitude of the digital filter. | + | *The two conditions after subtasks '''(2)''' and '''(3)''' only refer to the magnitude of the digital filter. |
*There is no constraint for the phase of the digital filter. | *There is no constraint for the phase of the digital filter. | ||
| − | *This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results. | + | *This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results. |
| − | *In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration. | + | *In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration. |
| − | The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see: | + | The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see: |
| − | [[File:EN_Mob_A_1_5d.png|right|frame|Approximation of the Jakes spectrum and | + | [[File:EN_Mob_A_1_5d.png|right|frame|Approximation of the Jakes spectrum and the auto-correlation function]] |
| − | + | * The Jakes PDS (left graph) can only be reproduced very inaccurately due to the vertical drop at $± f_{\rm D, \ max}$. | |
| − | * The Jakes | + | * For the time domain, this means that the ACF decreases much faster than the theory suggests. |
| − | * For the time domain, this means that the ACF decreases much faster than theory suggests. | + | *For small values of $\Delta t$, however, the approximation is very good (right graph). |
| − | *For small values of $\ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^1.3 Rayleigh Fading with Memory^]] |
Latest revision as of 12:41, 17 February 2022
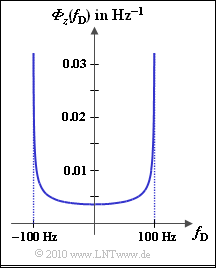
In a mobile radio system, the Doppler effect is also noticeable in the power-spectral density of the Doppler frequency $f_{\rm D}$.
This results in the so-called Jakes spectrum, which is shown in the graph for the maximum Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$. ${\it \Phi}_z(f_{\rm D})$ has only portions within the range $± f_{\rm D, \ max}$, where
- $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.1cm} max})^2} } \hspace{0.05cm}.$$
What is expressed in the frequency domain by the power-spectral density $\rm (PSD)$ is described in the time domain by the auto-correlation function $\rm (ACF)$. The ACF is the ${\it \Phi}_z(f_{\rm D})$ by the inverse Fourier transform of the PDS.
With the Bessel function of the first kind and zero order $({\rm J}_0)$ you get
- $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$
To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the Rayleigh channel model, each with the frequency response $H_{\rm DF}(f_{\rm D})$.
The dimensioning of these filters is part of this task.
- We restrict ourselves here to the branch for generating the real part $x(t)$. The ratios derived here are also valid for the imaginary part $y(t)$.
- At the input of the left digital filter of the Rayleigh channel model , there is white Gaussian noise $n(t)$ with variance $\sigma^2 = 0.5$.
- The real component is then obtained from the following convolution
- $$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$
Notes:
- This task belongs to the topic of Statistical bindings within the Rayleigh process.
- The digital filter is treated in detail in chapter Digital Filter of the book "Stochastic Signal Theory".
Questions
Solution
- $${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} \hspace{0.05cm}.$$
(2) Solution 2 is correct:
- The input signal $n(t)$ has a white (constant) PDS ${\it \Phi}_n(f_{\rm D})$.
- The PDS at the output is then
- $${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 \hspace{0.05cm}.$$
(3) Solution 3 is correct.
- Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$.
(4) No:
- The two conditions after subtasks (2) and (3) only refer to the magnitude of the digital filter.
- There is no constraint for the phase of the digital filter.
- This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results.
- In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration.
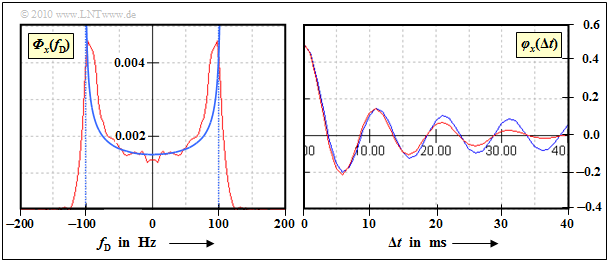
The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see:
- The Jakes PDS (left graph) can only be reproduced very inaccurately due to the vertical drop at $± f_{\rm D, \ max}$.
- For the time domain, this means that the ACF decreases much faster than the theory suggests.
- For small values of $\Delta t$, however, the approximation is very good (right graph).