Difference between revisions of "Aufgaben:Exercise 5.5Z: Complexity of the FFT"
m (Text replacement - "Category:Aufgaben zu Signaldarstellung" to "Category:Exercises for Signal Representation") |
|||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fast_Fourier_Transform_(FFT) |
}} | }} | ||
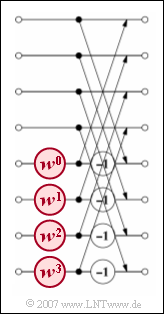
| − | [[File:P_ID1179__Sig_Z_5_5.png|right|frame| | + | [[File:P_ID1179__Sig_Z_5_5.png|right|frame|Final step of the FFT for $N=8$]] |
| − | + | The $\rm FFT$ algorithm ("Fast Fourier Transform") realises a "Discrete Fourier Transform" $\rm (DFT)$ with the smallest possible computational effort if the parameter $N$ is a power of two. In detail, the following calculation steps are necessary to carry out an FFT: | |
| − | * | + | *The FFT occurs in ${\rm log_2} \ N$ stages, whereby the exact same number of arithmetic operations must be carried out in each stage. |
| − | * | + | *The diagram shows the third and last stage for the example $N = 8$. It can be seen that $N/2$ basic operations have to be carried out in this and the other stages. |
| − | *In | + | *In each basic operation called '''butterfly''', two complex outputs are calculated from the two complex input variables $E_1$ and $E_2$ : |
:$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$ | :$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$ | ||
:$$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$ | :$$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$ | ||
| − | * | + | *Here $w = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi/N}$ denotes the complex rotation factor. For $N = 8$ the value $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}$ is obtained. |
| − | * | + | *The exponent $\mu$ for this complex rotation factor can take all integer values between $0$ and $N/2-1$. For $N = 8$ it is: |
:$$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} | :$$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} | ||
\cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm | \cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm | ||
| Line 17: | Line 17: | ||
\cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$ | \cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$ | ||
| − | + | The purpose of this task is to determine the number of arithmetic operations $(\mathcal{O}_{\rm FFT})$ required for the FFT and compare it with the value $\mathcal{O}_{\rm DFT} ≈ 8\cdot N^2$ that can be specified for the DFT. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Hints:'' | |
| − | + | *This task belongs to the chapter [[Signal_Representation/Fast_Fourier_Transform_(FFT)|Fast Fourier Transform (FFT)]]. | |
| − | + | *It makes sense to calculate the powers of $w$ before the actual algorithm and store them in a lookup table. The operations necessary for this are to be disregarded. | |
| − | '' | + | *The "bit reversal operation" – a rearrangement that has to be carried out before the first stage – is also not to be taken into account in this estimation. |
| − | * | ||
| Line 37: | Line 32: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many real additions $(A_{\rm A})$ does a complex addition require? |
|type="{}"} | |type="{}"} | ||
$A_{\rm A} \hspace{0.3cm} = \ $ { 2 } | $A_{\rm A} \hspace{0.3cm} = \ $ { 2 } | ||
| − | { | + | {How many real additions $(A_{\rm M})$ and multiplications $(M_{\rm M})$ are required for a complex multiplication? |
|type="{}"} | |type="{}"} | ||
$A_{\rm M} \hspace{0.3cm} = \ $ { 2 } | $A_{\rm M} \hspace{0.3cm} = \ $ { 2 } | ||
$M_{\rm M} \hspace{0.2cm} = \ $ { 4 } | $M_{\rm M} \hspace{0.2cm} = \ $ { 4 } | ||
| − | { | + | {How many complex additions/subtractions $(a_{\rm B})$ does a single basic operationn ("butterfly") require? |
| − | <br> | + | <br>How many complex multiplications $(m_{\rm B})$ are required per basic operation? |
|type="{}"} | |type="{}"} | ||
$a_{\rm B} \hspace{0.32cm} = \ $ { 2 } | $a_{\rm B} \hspace{0.32cm} = \ $ { 2 } | ||
$m_{\rm B} \hspace{0.2cm} = \ $ { 1 } | $m_{\rm B} \hspace{0.2cm} = \ $ { 1 } | ||
| − | { | + | {How many arithmetic operations (additions, subtractions, multiplications alike) does a basic operation require? |
|type="{}"} | |type="{}"} | ||
$\mathcal{O}_{\rm B} \ = \ $ { 10 } | $\mathcal{O}_{\rm B} \ = \ $ { 10 } | ||
| − | { | + | {How many real operations $(\mathcal{O}_{\rm FFT})$ does the entire FFT–algorithm require? What are the values for $N = 16$ und $N = 1024$? |
|type="{}"} | |type="{}"} | ||
$N = 16\text{:} \hspace{0.65cm} \mathcal{O}_{\rm FFT} \ = \ $ { 320 3% } | $N = 16\text{:} \hspace{0.65cm} \mathcal{O}_{\rm FFT} \ = \ $ { 320 3% } | ||
$N = 1024\text{:} \hspace{0.2cm} \mathcal{O}_{\rm FFT} \ = \ $ { 51200 3% } | $N = 1024\text{:} \hspace{0.2cm} \mathcal{O}_{\rm FFT} \ = \ $ { 51200 3% } | ||
| − | { | + | {What is the time gain $G_{\rm FFT} = \mathcal{O}_{\rm DFT} - \mathcal{O}_{\rm FFT}$ for $N = 16$ and $N = 1024$? |
|type="{}"} | |type="{}"} | ||
$N = 16\text{:} \hspace{0.65cm} G_{\rm FFT} \ = \ $ { 6.4 3% } | $N = 16\text{:} \hspace{0.65cm} G_{\rm FFT} \ = \ $ { 6.4 3% } | ||
| Line 71: | Line 66: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Each complex addition requires two real additions: |
:$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | :$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | ||
R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 80: | Line 75: | ||
| − | '''(2)''' | + | '''(2)''' Any complex multiplication requires four real multiplications and two real additions: |
:$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot | :$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot | ||
R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | ||
| Line 88: | Line 83: | ||
| − | '''(3)''' | + | '''(3)''' The basic operations with complex inputs $E_1$, $E_2$ and $w^{\hspace{0.04cm}\mu}$ are: |
:$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu},\hspace{0.5cm} A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$ | :$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu},\hspace{0.5cm} A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$ | ||
| − | * | + | *This means one complex multiplication and two complex additions: $\hspace{0.15 cm}\underline{a_{\rm B} = 2, \hspace{0.2cm}m_{\rm B} = 1} |
\hspace{0.05cm}.$ | \hspace{0.05cm}.$ | ||
| − | '''(4)''' | + | '''(4)''' In contrast to the first computers, a multiplication today does not take much more computing time than an addition or subtraction. |
| − | * | + | *Using the results of subtasks '''(1)''', '''(2)''' and '''(3)''' we obtain for the total number of arithmetic operations: |
:$$ \mathcal{O}_{\rm B} = a_{\rm B}\cdot A_{\rm A} + a_{\rm B}\cdot (A_{\rm M} | :$$ \mathcal{O}_{\rm B} = a_{\rm B}\cdot A_{\rm A} + a_{\rm B}\cdot (A_{\rm M} | ||
+M_{\rm M} ) = 2 \cdot 2 + 1 \cdot 6\hspace{0.15 cm}\underline{ = 10} | +M_{\rm M} ) = 2 \cdot 2 + 1 \cdot 6\hspace{0.15 cm}\underline{ = 10} | ||
| Line 102: | Line 97: | ||
| − | '''(5)''' | + | '''(5)''' There are ${\rm log_2} \ N$ stages in total, each of which requires $N/2$ basic operations to be performed: |
:$$\mathcal{O}_{\rm FFT} = {\rm log_2}\hspace{0.1cm}N \cdot \frac{N}{2}\cdot | :$$\mathcal{O}_{\rm FFT} = {\rm log_2}\hspace{0.1cm}N \cdot \frac{N}{2}\cdot | ||
\mathcal{O}_{\rm B} = 5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N$$ | \mathcal{O}_{\rm B} = 5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N$$ | ||
| Line 111: | Line 106: | ||
| − | '''(6)''' | + | '''(6)''' The computational time gain of the FFT over the conventional DFT is given by: |
:$$G_{\rm FFT} = \frac{\mathcal{O}_{\rm DFT}}{\mathcal{O}_{\rm FFT}} = \frac{8 \cdot N^2} {5 \cdot | :$$G_{\rm FFT} = \frac{\mathcal{O}_{\rm DFT}}{\mathcal{O}_{\rm FFT}} = \frac{8 \cdot N^2} {5 \cdot | ||
N \cdot {\rm log_2}\hspace{0.1cm}N }= 1.6 \cdot \frac{N}{ {\rm | N \cdot {\rm log_2}\hspace{0.1cm}N }= 1.6 \cdot \frac{N}{ {\rm | ||
| Line 124: | Line 119: | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.5 Fast Fourier Transform ^]] |
Latest revision as of 15:48, 24 May 2021
The $\rm FFT$ algorithm ("Fast Fourier Transform") realises a "Discrete Fourier Transform" $\rm (DFT)$ with the smallest possible computational effort if the parameter $N$ is a power of two. In detail, the following calculation steps are necessary to carry out an FFT:
- The FFT occurs in ${\rm log_2} \ N$ stages, whereby the exact same number of arithmetic operations must be carried out in each stage.
- The diagram shows the third and last stage for the example $N = 8$. It can be seen that $N/2$ basic operations have to be carried out in this and the other stages.
- In each basic operation called butterfly, two complex outputs are calculated from the two complex input variables $E_1$ and $E_2$ :
- $$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$
- $$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$
- Here $w = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi/N}$ denotes the complex rotation factor. For $N = 8$ the value $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}$ is obtained.
- The exponent $\mu$ for this complex rotation factor can take all integer values between $0$ and $N/2-1$. For $N = 8$ it is:
- $$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm j},\hspace{0.2cm}w^3 = -{1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$
The purpose of this task is to determine the number of arithmetic operations $(\mathcal{O}_{\rm FFT})$ required for the FFT and compare it with the value $\mathcal{O}_{\rm DFT} ≈ 8\cdot N^2$ that can be specified for the DFT.
Hints:
- This task belongs to the chapter Fast Fourier Transform (FFT).
- It makes sense to calculate the powers of $w$ before the actual algorithm and store them in a lookup table. The operations necessary for this are to be disregarded.
- The "bit reversal operation" – a rearrangement that has to be carried out before the first stage – is also not to be taken into account in this estimation.
Questions
Solution
- $$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15 cm}\underline{ A_{\rm A} = 2}\hspace{0.05cm}.$$
(2) Any complex multiplication requires four real multiplications and two real additions:
- $$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{A_{\rm M} = 2,\hspace{0.3cm}M_{\rm M} = 4} \hspace{0.05cm}.$$
(3) The basic operations with complex inputs $E_1$, $E_2$ and $w^{\hspace{0.04cm}\mu}$ are:
- $$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu},\hspace{0.5cm} A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$
- This means one complex multiplication and two complex additions: $\hspace{0.15 cm}\underline{a_{\rm B} = 2, \hspace{0.2cm}m_{\rm B} = 1} \hspace{0.05cm}.$
(4) In contrast to the first computers, a multiplication today does not take much more computing time than an addition or subtraction.
- Using the results of subtasks (1), (2) and (3) we obtain for the total number of arithmetic operations:
- $$ \mathcal{O}_{\rm B} = a_{\rm B}\cdot A_{\rm A} + a_{\rm B}\cdot (A_{\rm M} +M_{\rm M} ) = 2 \cdot 2 + 1 \cdot 6\hspace{0.15 cm}\underline{ = 10} \hspace{0.05cm}.$$
(5) There are ${\rm log_2} \ N$ stages in total, each of which requires $N/2$ basic operations to be performed:
- $$\mathcal{O}_{\rm FFT} = {\rm log_2}\hspace{0.1cm}N \cdot \frac{N}{2}\cdot \mathcal{O}_{\rm B} = 5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N$$
- $$\Rightarrow \hspace{0.3cm}\mathcal{O}_{\rm FFT}\hspace{0.1cm}(N=16) = 5\cdot 16 \cdot 4 \hspace{0.15 cm}\underline{= 320}, \hspace{0.5cm}\mathcal{O}_{\rm FFT}\hspace{0.1cm}(N=1024) = 5\cdot 1024 \cdot 10 \hspace{0.15 cm}\underline{= 51200} \hspace{0.05cm}.$$
(6) The computational time gain of the FFT over the conventional DFT is given by:
- $$G_{\rm FFT} = \frac{\mathcal{O}_{\rm DFT}}{\mathcal{O}_{\rm FFT}} = \frac{8 \cdot N^2} {5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N }= 1.6 \cdot \frac{N}{ {\rm log_2}\hspace{0.1cm}N}$$
- $$\Rightarrow \hspace{0.3cm}G_{\rm FFT} \hspace{0.1cm}(N=16) = 1.6 \cdot \frac{16}{ 4} \hspace{0.15 cm}\underline{= 6.4}, \hspace{0.5cm}G_{\rm FFT} \hspace{0.1cm}(N=1024) = 1.6 \cdot\frac{1024}{ 10}\hspace{0.15 cm}\underline{ \approx 164} \hspace{0.05cm}.$$