Difference between revisions of "Aufgaben:Exercise 1.5Z: Sinc-shaped Impulse Response"
From LNTwww
m (Text replacement - "Signal_Representation/Fouriertransformation_und_-rücktransformation" to "Signal_Representation/Fourier_Transform_and_Its_Inverse") |
|||
| (25 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
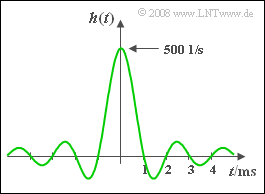
| − | [[File:P_ID857__LZI_Z_1_5.png|right|frame|$\rm | + | [[File:P_ID857__LZI_Z_1_5.png|right|frame|$\rm sinc$–shaped impulse response]] |
| − | + | The impulse response of a linear time-invariant (and non-causal) system was determined as follows (see graph): | |
| − | :$$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm | + | :$$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm sinc}\big[{t}/({ 1\hspace{0.1cm}{\rm ms}})\big] .$$ |
| − | + | The output signals $y(t)$ should be computed if various cosine oscillations of different frequency $f_0$ are applied to the input: | |
| − | |||
:$$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 | :$$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 | ||
\cdot t ) .$$ | \cdot t ) .$$ | ||
| Line 18: | Line 17: | ||
| − | '' | + | ''Please note:'' |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. |
| − | * | + | *The solution can be found in the time domain or in the frequency domain. In the sample solution you will find both approaches. |
| − | * | + | *The following definite integral is given: |
:$$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm | :$$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm | ||
d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad | d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad | ||
| Line 31: | Line 30: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the frequency response $H(f)$ of the LTI system. What is the equivalent bandwidth and the direct signal (DC) transmission factor? |
|type="{}"} | |type="{}"} | ||
$\Delta f \ =\ $ { 1 3% } $\ \rm kHz$ | $\Delta f \ =\ $ { 1 3% } $\ \rm kHz$ | ||
| Line 40: | Line 39: | ||
| − | { | + | {What is the signal value of the output signal $y(t)$ at time $t = 0$ if the input is cosine-shaped and of frequency $\underline{f_0 = 1\ \rm kHz}$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { 0. } $\ \rm V$ | $y(t = 0) \ = \ $ { 0. } $\ \rm V$ | ||
| − | { | + | {What is the signal value of the output signal $y(t)$ at time $t = 0$ if the input is cosine-shaped and of frequency $\underline{f_0 = 0.1\ \rm kHz}$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ =\ $ { 2 3% } $\ \rm V$ | $y(t = 0) \ =\ $ { 2 3% } $\ \rm V$ | ||
| − | { | + | {What is the signal value of the output signal $y(t)$ at timee $t = 0$ if the input is cosine-shaped and of frequency $\underline{f_0 = 0.5\ \rm kHz}$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ = \ $ { 1 3% } $\ \rm V$ | $y(t = 0) \ = \ $ { 1 3% } $\ \rm V$ | ||
| Line 56: | Line 55: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' A comparison with the equations on the page [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Ideal_low-pass_filter_–_Rectangular-in-frequency|Ideal low-pass filter]] or applying the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#The_second_Fourier_integral |inverse Fourier transformation]] shows that $H(f)$ is an ideal low-pass filter: |
:$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm}K \\ K/2 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} | :$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm}K \\ K/2 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} | ||
\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} | \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} | ||
| Line 65: | Line 64: | ||
{\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ | {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | * | + | *The equidistant zero-crossings of the impulse response occur at an interval of $Δt = 1 \ \rm ms$ . |
| − | * | + | *From this it follows that the equivalent bandwidth is $Δf \rm \underline{ = 1 \ \rm kHz}$. |
| − | * | + | *If $K = 1$ was true, then $h(0) = Δf = 1000 \cdot \rm 1/s$ should hold. |
| − | * | + | *Because of the given $h(0) = 500 \cdot{\rm 1/s} = Δf/2$ the direct signal (DC) transmission factor thus is $K = H(f = 0) \; \rm \underline{= 0.5}$. |
| − | '''(2)''' | + | '''(2)''' This problem is most easily solved in the spectral domain. |
| − | * | + | *For the output spectrum the following holds: $Y(f) = X(f)\cdot H(f) .$ |
| − | *$X(f)$ | + | *$X(f)$ consists of two Dirac functions at $± f_0$ each with weight $A_x/2 =2 \hspace{0.08cm}\rm V$. |
| − | * | + | *For $f = f_0 = 1 \ {\rm kHz} > Δf/2$ , however $H(f) = 0$ holds, such that $Y(f) = 0$ and hence also $y(t) = 0$ ⇒ $\underline{y(t = 0) = 0}$. |
| − | + | The solution in the time domain is based on convolution: | |
:$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {h ( \tau )} \cdot | :$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {h ( \tau )} \cdot | ||
x ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | x ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *At time $t = 0$ the following is obtained considering the symmetry of the cosine function: |
:$$y(t = 0 ) = \frac{A_x \cdot \Delta f}{2} \cdot \int_{ - \infty }^{ + \infty } {\rm si} ( \pi \cdot \Delta f \cdot \tau ) \cdot | :$$y(t = 0 ) = \frac{A_x \cdot \Delta f}{2} \cdot \int_{ - \infty }^{ + \infty } {\rm si} ( \pi \cdot \Delta f \cdot \tau ) \cdot | ||
{\rm cos}(2\pi \cdot f_0 | {\rm cos}(2\pi \cdot f_0 | ||
\cdot \tau ) \hspace{0.1cm}{\rm d}\tau.$$ | \cdot \tau ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *With the substitution $u = π · Δf · τ$ , this can also be formulated as follows: |
:$$y(t = 0 ) = \frac{A_x }{\pi} \cdot \int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u .$$ | :$$y(t = 0 ) = \frac{A_x }{\pi} \cdot \int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u .$$ | ||
| − | * | + | *Here, the constant is $a = 2f_0/Δf = 2$. With this value, the given integral yields zero: $y(t = 0 ) = {A_y } = 0.$ |
| − | '''(3)''' | + | '''(3)''' The frequency response has the value $K = 0.5$ at $f = f_0 = 100 \ \rm Hz$ according to the calculations for subtask '''(1)''' . Therefore, |
| − | :$$A_y = A_x/2 = 2\ \rm V | + | :$$A_y = A_x/2 = 2\ \rm V$$ is obtained. |
| − | * | + | *The same result is obtained by convolution according to the above equation. |
| − | * | + | *For $a = 2f_0/Δf = 0.2$ the integral is equal to $π/2$ and one obtains |
:$$y(t = 0 ) = {A_y } = \frac{A_x}{\pi} \cdot \frac{\pi}{2} = \frac{A_x}{2} \hspace{0.15cm}\underline{= 2\,{\rm V}}.$$ | :$$y(t = 0 ) = {A_y } = \frac{A_x}{\pi} \cdot \frac{\pi}{2} = \frac{A_x}{2} \hspace{0.15cm}\underline{= 2\,{\rm V}}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The transition from the band-pass to the band-stop is exactly at $f = 0.5 \ \rm kHz$ and for this singular location the following holds: |
:$$H(f = f_0) = K/2.$$ | :$$H(f = f_0) = K/2.$$ | ||
| − | * | + | *Thus, the amplitude of the output signal is only half as large as calculated in subtask '''(3)''' , namely $A_y \; \underline{= 1 \, \rm V}$. |
| − | * | + | *The same result is obtained with $a = 2f_0/Δf = 1$ by convolution. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.3 Some Low-Pass Functions in Systems Theory^]] |
Latest revision as of 13:54, 7 September 2021
The impulse response of a linear time-invariant (and non-causal) system was determined as follows (see graph):
- $$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm sinc}\big[{t}/({ 1\hspace{0.1cm}{\rm ms}})\big] .$$
The output signals $y(t)$ should be computed if various cosine oscillations of different frequency $f_0$ are applied to the input:
- $$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 \cdot t ) .$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- The solution can be found in the time domain or in the frequency domain. In the sample solution you will find both approaches.
- The following definite integral is given:
- $$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ |a| < 1,} \\{ |a| = 1,} \\ { |a| > 1.} \\ \end{array}$$
Questions
Solution
(1) A comparison with the equations on the page Ideal low-pass filter or applying the inverse Fourier transformation shows that $H(f)$ is an ideal low-pass filter:
- $$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm}K \\ K/2 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.005cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$
- The equidistant zero-crossings of the impulse response occur at an interval of $Δt = 1 \ \rm ms$ .
- From this it follows that the equivalent bandwidth is $Δf \rm \underline{ = 1 \ \rm kHz}$.
- If $K = 1$ was true, then $h(0) = Δf = 1000 \cdot \rm 1/s$ should hold.
- Because of the given $h(0) = 500 \cdot{\rm 1/s} = Δf/2$ the direct signal (DC) transmission factor thus is $K = H(f = 0) \; \rm \underline{= 0.5}$.
(2) This problem is most easily solved in the spectral domain.
- For the output spectrum the following holds: $Y(f) = X(f)\cdot H(f) .$
- $X(f)$ consists of two Dirac functions at $± f_0$ each with weight $A_x/2 =2 \hspace{0.08cm}\rm V$.
- For $f = f_0 = 1 \ {\rm kHz} > Δf/2$ , however $H(f) = 0$ holds, such that $Y(f) = 0$ and hence also $y(t) = 0$ ⇒ $\underline{y(t = 0) = 0}$.
The solution in the time domain is based on convolution:
- $$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {h ( \tau )} \cdot x ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- At time $t = 0$ the following is obtained considering the symmetry of the cosine function:
- $$y(t = 0 ) = \frac{A_x \cdot \Delta f}{2} \cdot \int_{ - \infty }^{ + \infty } {\rm si} ( \pi \cdot \Delta f \cdot \tau ) \cdot {\rm cos}(2\pi \cdot f_0 \cdot \tau ) \hspace{0.1cm}{\rm d}\tau.$$
- With the substitution $u = π · Δf · τ$ , this can also be formulated as follows:
- $$y(t = 0 ) = \frac{A_x }{\pi} \cdot \int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u .$$
- Here, the constant is $a = 2f_0/Δf = 2$. With this value, the given integral yields zero: $y(t = 0 ) = {A_y } = 0.$
(3) The frequency response has the value $K = 0.5$ at $f = f_0 = 100 \ \rm Hz$ according to the calculations for subtask (1) . Therefore,
- $$A_y = A_x/2 = 2\ \rm V$$ is obtained.
- The same result is obtained by convolution according to the above equation.
- For $a = 2f_0/Δf = 0.2$ the integral is equal to $π/2$ and one obtains
- $$y(t = 0 ) = {A_y } = \frac{A_x}{\pi} \cdot \frac{\pi}{2} = \frac{A_x}{2} \hspace{0.15cm}\underline{= 2\,{\rm V}}.$$
(4) The transition from the band-pass to the band-stop is exactly at $f = 0.5 \ \rm kHz$ and for this singular location the following holds:
- $$H(f = f_0) = K/2.$$
- Thus, the amplitude of the output signal is only half as large as calculated in subtask (3) , namely $A_y \; \underline{= 1 \, \rm V}$.
- The same result is obtained with $a = 2f_0/Δf = 1$ by convolution.