Difference between revisions of "Aufgaben:Exercise 5.4Z: On the Hanning Window"
m (Text replacement - "Signaldarstellung/Spektralanalyse" to "Signal_Representation/Spectrum_Analysis") |
|||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1168__Sig_Z_5_4.png|250px|right|frame| | + | [[File:P_ID1168__Sig_Z_5_4.png|250px|right|frame|Characterisation of the Hanning window]] |
| − | In | + | In this task, important properties of the frequently used Hanning window are to be derived. The continuous-time representation in the interval from $-T_{\rm P}/2$ to $+T_{\rm P}/2$ is here as follows: |
:$$w(t)= {\rm cos}^2(\pi \cdot | :$$w(t)= {\rm cos}^2(\pi \cdot | ||
{t}/{T_{\rm P}})= 0.5\cdot \big(1 + {\rm cos}(2\pi \cdot | {t}/{T_{\rm P}})= 0.5\cdot \big(1 + {\rm cos}(2\pi \cdot | ||
{t}/{T_{\rm P}}) \big ) | {t}/{T_{\rm P}}) \big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Outside the symmetric time domain of duration $T_{\rm P}$: $w(t) \equiv 0$. | |
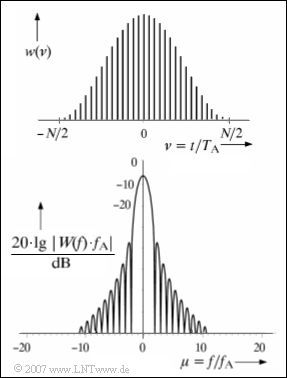
| − | + | The upper graph shows the discrete-time representation $w(\nu) = w({\nu} \cdot T_{\rm A})$, where $T_{\rm A}$ is smaller than $T_{\rm P}$ by a factor $N = 32$. The definition range of the discrete time variable $ν$ extends from $-16$ to $+15$. | |
| − | In | + | In the lower graph, the Fourier transform $W(f)$ of the continuous-time window function $w(t)$ is shown logarithmically. The abscissa is normalised to $f_{\rm A} = 1/T_{\rm P}$. One can see: |
| − | * | + | *The equidistant values $W({\mu} \cdot f_{\rm A})$ are zero except for $μ = 0$ and $μ = ±1$. |
| − | * | + | *The main lobe thus extends to the frequency range $|f| ≤ 2 · f_{\rm A}$. |
| − | *$W(f)$ | + | *$W(f)$ is largest in magnitude outside the main lobe for $f = ±2.5 · f_{\rm A}$. |
| − | * | + | *Thus, the minimum distance between the main and the side lobes applies here: |
| − | :$$ | + | :$$D_{\text{min (main lobe / side lobes) } } = 20 \cdot {\rm lg}\hspace{0.15cm} |
\frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} \hspace{0.15cm}{\rm (in}\hspace{0.1cm}{\rm dB)}\hspace{0.05cm}.$$ | \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} \hspace{0.15cm}{\rm (in}\hspace{0.1cm}{\rm dB)}\hspace{0.05cm}.$$ | ||
| Line 30: | Line 30: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This task belongs to the chapter [[Signal_Representation/Spectrum_Analysis|Spectral Analysis]]. |
| − | * | + | *Note that the frequency resolution $f_{\rm A}$ is equal to the reciprocal of the adjustable parameter $T_{\rm P}$. |
| + | *In this exercise we use the ${\rm si}$–function: ${\rm si}(x) = \sin(x)/x$. | ||
| Line 38: | Line 39: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the discrete-time coefficients $w(ν)$ of the Hanning window analytically. What are the numerical values for $ν = 0$, $ν = 1$ and $ν = -\hspace{0.05cm}8$? |
|type="{}"} | |type="{}"} | ||
$w(ν = 0) \hspace{0.37cm} = \ $ { 1 1% } | $w(ν = 0) \hspace{0.37cm} = \ $ { 1 1% } | ||
| Line 48: | Line 49: | ||
$w(ν = -8) \hspace{0.03cm} = \ $ { 0.5 1% } | $w(ν = -8) \hspace{0.03cm} = \ $ { 0.5 1% } | ||
| − | { | + | {Calculate the spectral function $W(f)$ in general. Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - $W(f)$ | + | - $W(f)$ yields complex results for special frequency values. |
| − | + $W(f)$ | + | + $W(f)$ is even with respect to $f$ , i.e. $W(-f) = W(+f)$. |
| − | + | + | + The spectral value $W(f = 0)=0.5/f_{\rm A}$ and thus real. |
| − | { | + | {What are $W(f = ±f_{\rm A})$ and the $\text{6dB}$ bandwidth normalised to $f_{\rm A}$? |
|type="{}"} | |type="{}"} | ||
$W(±f_{\rm A}) \hspace{0.15cm} = \ $ { 0.25 1% } $\ \cdot \ 1/f_{\rm A}$ | $W(±f_{\rm A}) \hspace{0.15cm} = \ $ { 0.25 1% } $\ \cdot \ 1/f_{\rm A}$ | ||
$B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \hspace{0.2cm} = \ $ { 2 1% } | $B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \hspace{0.2cm} = \ $ { 2 1% } | ||
| − | { | + | {What is the minimum distance between the main lobe and the side lobes. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $D_{\text{min (main lobe / side lobes) } } \ = \ $ { 32.3 1% } $\ \rm dB$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' After trigonometric transformation, the result for the continuous-time window function is: |
:$$w(t) = {\rm cos}^2(\pi \cdot | :$$w(t) = {\rm cos}^2(\pi \cdot | ||
{t}/{T_{\rm P}}) = 0.5+ 0.5\cdot {\rm | {t}/{T_{\rm P}}) = 0.5+ 0.5\cdot {\rm | ||
cos}(2\pi \cdot {t}/{T_{\rm P}})\hspace{0.05cm}.$$ | cos}(2\pi \cdot {t}/{T_{\rm P}})\hspace{0.05cm}.$$ | ||
| − | * | + | *After time discretisation with $ν = t/T_{\rm A}$ and $T_{\rm P}/T_{\rm A} = N = 32$, one obtains for the discrete-time window: |
:$$w(\nu) = w(\nu \cdot T_{\rm A}) = 0.5+ 0.5\cdot {\rm | :$$w(\nu) = w(\nu \cdot T_{\rm A}) = 0.5+ 0.5\cdot {\rm | ||
cos}(2\pi \cdot {\nu}/{N})\hspace{0.8cm} | cos}(2\pi \cdot {\nu}/{N})\hspace{0.8cm} | ||
| Line 83: | Line 84: | ||
| − | '''(2)''' | + | '''(2)''' The correct <u>solutions are 2 and 3:</u>: |
| − | * | + | *The periodic continuation of $w(t)$ corresponding to the period $T_{\rm P}$ yields a (periodic) signal with a DC and a cosine component. |
| − | * | + | *From this follows with $f_{\rm A} = 1/T_{\rm P}$: |
:$${\rm P}\{w(t)\} = 0.5+0.5\cdot {\rm | :$${\rm P}\{w(t)\} = 0.5+0.5\cdot {\rm | ||
cos}(2\pi \cdot f_{\rm A} \cdot t) | cos}(2\pi \cdot f_{\rm A} \cdot t) | ||
| Line 91: | Line 92: | ||
\hspace{0.2cm}0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm | \hspace{0.2cm}0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm | ||
\delta}(f \pm f_{\rm A}))\hspace{0.05cm}.$$ | \delta}(f \pm f_{\rm A}))\hspace{0.05cm}.$$ | ||
| − | * | + | *The time-limited signal $w(t)$ is obtained from ${\rm P}\{w(t)\}$ by multiplication with a rectangle of amplitude $1$ and duration $T_{\rm P}$. |
| − | * | + | *Its spectrum $W(f)$ is thus obtained from the convolution of the above spectral function with the function $T_{\rm P} · {\rm si}(π \cdot f \cdot T_{\rm P}) = 1/f_{\rm A} · {\rm si}(π \cdot f/f_{\rm A})$: |
:$$w(t) | :$$w(t) | ||
\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, | ||
| Line 99: | Line 100: | ||
\frac{f-f_{\rm A}}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm | \frac{f-f_{\rm A}}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm | ||
si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$ | si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$ | ||
| − | * | + | *This spectral function is even and also real for all frequencies $f$ . The spectral value at frequency $f = 0$ gives the window area: |
:$$W(f=0) = | :$$W(f=0) = | ||
\frac{0.5}{f_{\rm A}}= | \frac{0.5}{f_{\rm A}}= | ||
| Line 107: | Line 108: | ||
| − | '''(3)''' | + | '''(3)''' From the result of sub-task '''(2)''' it also follows: |
:$$W(f = ±f_{\rm A}) = W(0)/2\hspace{0.15cm}\underline{ = 0.25} \cdot 1/{f_{\rm A}}.$$ | :$$W(f = ±f_{\rm A}) = W(0)/2\hspace{0.15cm}\underline{ = 0.25} \cdot 1/{f_{\rm A}}.$$ | ||
| − | * | + | *Due to the monotonic course in the range $|f| < f_{\rm A}$ , the magnitude function $|W(f)|$ has dropped to half of the maximum for the first time exactly at $± f_{\rm A}$ . |
| − | * | + | *Thus, $B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \;\underline{=2}$. |
| − | '''(4)''' | + | '''(4)''' The largest spectral magnitude outside the main lobe occurs at $f = ±2.5 f_{\rm A}$. With the result of subtask '''(2)''' holds: |
:$$W(f = 2.5 \cdot f_{\rm A}) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}(2.5 \pi ) | :$$W(f = 2.5 \cdot f_{\rm A}) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}(2.5 \pi ) | ||
+\frac{0.25}{f_{\rm A}}\cdot {\rm si}(1.5 \pi )+\frac{0.25}{f_{\rm A}}\cdot {\rm si}(3.5 \pi )= \frac{0.25}{\pi \cdot f_{\rm A}}\left[ \frac{2}{2.5}-\frac{1}{1.5}-\frac{1}{3.5}\right] \approx -\frac{0.0121}{ f_{\rm A}}\hspace{0.05cm}.$$ | +\frac{0.25}{f_{\rm A}}\cdot {\rm si}(1.5 \pi )+\frac{0.25}{f_{\rm A}}\cdot {\rm si}(3.5 \pi )= \frac{0.25}{\pi \cdot f_{\rm A}}\left[ \frac{2}{2.5}-\frac{1}{1.5}-\frac{1}{3.5}\right] \approx -\frac{0.0121}{ f_{\rm A}}\hspace{0.05cm}.$$ | ||
| − | * | + | *This gives the minimum distance between the main lobe and the side lobes: |
| − | :$$ | + | :$$D_{\text{min (main lobe / side lobes) } } = 20 \cdot {\rm lg}\hspace{0.15cm} |
\frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} = 20 \cdot {\rm lg}\hspace{0.15cm} | \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} = 20 \cdot {\rm lg}\hspace{0.15cm} | ||
\frac{0.5}{0.0121}\hspace{0.15 cm}\underline{\approx 32.3\,\,{\rm dB}}\hspace{0.05cm}.$$ | \frac{0.5}{0.0121}\hspace{0.15 cm}\underline{\approx 32.3\,\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| Line 125: | Line 126: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.4 Spectrum Analysis^]] |
Latest revision as of 04:18, 18 September 2022
In this task, important properties of the frequently used Hanning window are to be derived. The continuous-time representation in the interval from $-T_{\rm P}/2$ to $+T_{\rm P}/2$ is here as follows:
- $$w(t)= {\rm cos}^2(\pi \cdot {t}/{T_{\rm P}})= 0.5\cdot \big(1 + {\rm cos}(2\pi \cdot {t}/{T_{\rm P}}) \big ) \hspace{0.05cm}.$$
Outside the symmetric time domain of duration $T_{\rm P}$: $w(t) \equiv 0$.
The upper graph shows the discrete-time representation $w(\nu) = w({\nu} \cdot T_{\rm A})$, where $T_{\rm A}$ is smaller than $T_{\rm P}$ by a factor $N = 32$. The definition range of the discrete time variable $ν$ extends from $-16$ to $+15$.
In the lower graph, the Fourier transform $W(f)$ of the continuous-time window function $w(t)$ is shown logarithmically. The abscissa is normalised to $f_{\rm A} = 1/T_{\rm P}$. One can see:
- The equidistant values $W({\mu} \cdot f_{\rm A})$ are zero except for $μ = 0$ and $μ = ±1$.
- The main lobe thus extends to the frequency range $|f| ≤ 2 · f_{\rm A}$.
- $W(f)$ is largest in magnitude outside the main lobe for $f = ±2.5 · f_{\rm A}$.
- Thus, the minimum distance between the main and the side lobes applies here:
- $$D_{\text{min (main lobe / side lobes) } } = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} \hspace{0.15cm}{\rm (in}\hspace{0.1cm}{\rm dB)}\hspace{0.05cm}.$$
Hints:
- This task belongs to the chapter Spectral Analysis.
- Note that the frequency resolution $f_{\rm A}$ is equal to the reciprocal of the adjustable parameter $T_{\rm P}$.
- In this exercise we use the ${\rm si}$–function: ${\rm si}(x) = \sin(x)/x$.
Questions
Solution
- $$w(t) = {\rm cos}^2(\pi \cdot {t}/{T_{\rm P}}) = 0.5+ 0.5\cdot {\rm cos}(2\pi \cdot {t}/{T_{\rm P}})\hspace{0.05cm}.$$
- After time discretisation with $ν = t/T_{\rm A}$ and $T_{\rm P}/T_{\rm A} = N = 32$, one obtains for the discrete-time window:
- $$w(\nu) = w(\nu \cdot T_{\rm A}) = 0.5+ 0.5\cdot {\rm cos}(2\pi \cdot {\nu}/{N})\hspace{0.8cm} \Rightarrow \hspace{0.3cm}w(\nu = 0) \hspace{0.15 cm}\underline{= 1},$$
- $$w(\nu = 1) = 0.5+ 0.5\cdot {\rm cos}( \frac{\pi}{16})\hspace{0.15 cm}\underline{ = 0.99}, $$
- $$w(\nu = -8)=0.5+ 0.5\cdot {\rm cos}( \frac{-\pi}{2}) \hspace{0.15 cm}\underline{= 0.5}\hspace{0.05cm}.$$
(2) The correct solutions are 2 and 3::
- The periodic continuation of $w(t)$ corresponding to the period $T_{\rm P}$ yields a (periodic) signal with a DC and a cosine component.
- From this follows with $f_{\rm A} = 1/T_{\rm P}$:
- $${\rm P}\{w(t)\} = 0.5+0.5\cdot {\rm cos}(2\pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm}0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm \delta}(f \pm f_{\rm A}))\hspace{0.05cm}.$$
- The time-limited signal $w(t)$ is obtained from ${\rm P}\{w(t)\}$ by multiplication with a rectangle of amplitude $1$ and duration $T_{\rm P}$.
- Its spectrum $W(f)$ is thus obtained from the convolution of the above spectral function with the function $T_{\rm P} · {\rm si}(π \cdot f \cdot T_{\rm P}) = 1/f_{\rm A} · {\rm si}(π \cdot f/f_{\rm A})$:
- $$w(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, W(f) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}( \frac{\pi f}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f-f_{\rm A}}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$
- This spectral function is even and also real for all frequencies $f$ . The spectral value at frequency $f = 0$ gives the window area:
- $$W(f=0) = \frac{0.5}{f_{\rm A}}= \int_{-\infty}^{+\infty}w(t)\hspace{0.05cm}{\rm d}t\hspace{0.05cm}.$$
(3) From the result of sub-task (2) it also follows:
- $$W(f = ±f_{\rm A}) = W(0)/2\hspace{0.15cm}\underline{ = 0.25} \cdot 1/{f_{\rm A}}.$$
- Due to the monotonic course in the range $|f| < f_{\rm A}$ , the magnitude function $|W(f)|$ has dropped to half of the maximum for the first time exactly at $± f_{\rm A}$ .
- Thus, $B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \;\underline{=2}$.
(4) The largest spectral magnitude outside the main lobe occurs at $f = ±2.5 f_{\rm A}$. With the result of subtask (2) holds:
- $$W(f = 2.5 \cdot f_{\rm A}) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}(2.5 \pi ) +\frac{0.25}{f_{\rm A}}\cdot {\rm si}(1.5 \pi )+\frac{0.25}{f_{\rm A}}\cdot {\rm si}(3.5 \pi )= \frac{0.25}{\pi \cdot f_{\rm A}}\left[ \frac{2}{2.5}-\frac{1}{1.5}-\frac{1}{3.5}\right] \approx -\frac{0.0121}{ f_{\rm A}}\hspace{0.05cm}.$$
- This gives the minimum distance between the main lobe and the side lobes:
- $$D_{\text{min (main lobe / side lobes) } } = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{0.5}{0.0121}\hspace{0.15 cm}\underline{\approx 32.3\,\,{\rm dB}}\hspace{0.05cm}.$$