Difference between revisions of "Signal Representation/The Convolution Theorem and Operation"
| (35 intermediate revisions by 4 users not shown) | |||
| Line 6: | Line 6: | ||
}} | }} | ||
| − | ==Convolution in | + | ==Convolution in the time domain== |
<br> | <br> | ||
| − | The & | + | The »Convolution Theorem« is one of the most important laws of the Fourier transform, to which an own subchapter is dedicated in this tutorial. We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known: |
| − | |||
| − | We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known: | ||
:$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | :$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | ||
| − | Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies: | + | Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies: |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | $\tau$ is a formal integration variable with the dimension of a time. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called '''convolution''' | + | $\text{Definition:}$ |
| + | |||
| + | The above connection of the time function $x_1(t)$ and $x_2(t)$ is called »'''convolution'''«. One represents this functional connection with a star: | ||
:$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$ | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$ | ||
| − | Thus the above Fourier correspondence can be written as follows: | + | *Thus the above Fourier correspondence can be written as follows: |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | ||
| − | The [[Signal_Representation/The_Convolution_Theorem_and_Operation# | + | *The convolution is »commutative« ⇒ The order of the operands can be changed: |
| + | |||
| + | :$$x_1(t) * x_2(t) =x_2(t) * x_1(t).$$ | ||
| + | |||
| + | *The [[Signal_Representation/The_Convolution_Theorem_and_Operation#Proof_of_the_Convolution_Theorem|»Proof«]] will be shown at the end of this chapter.}} | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | [[File:EN_Sig_T_3_4_S1.png|right|frame|On calculation of signal and spectrum of the LTI output]] | ||
| + | $\text{Example 1:}$ Every linear time-invariant $\rm (LTI)$ system can be described both, | ||
| + | #by the frequency response $H(f)$, | ||
| + | #by the impulse response $h(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | If | + | The relation between these two system quantities is also given by the Fourier transform. |
| + | |||
| + | *If the signal $x(t)$ with spectrum $X(f)$ is applied to the input, then the spectrum of the output signal is: | ||
:$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | :$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | ||
| − | It is possible to calculate the output signal in the time domain with the convolution theorem: | + | *It is possible to calculate the output signal in the time domain with the convolution theorem: |
:$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | :$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | ||
| − | This equation shows again | + | *This equation shows again the »commutativity« of the »convolution operation«. }} |
| − | ==Convolution in the | + | ==Convolution in the frequency domain== |
<br> | <br> | ||
The duality between time and frequency domain also allows statements regarding the spectrum of the product signal: | The duality between time and frequency domain also allows statements regarding the spectrum of the product signal: | ||
| Line 56: | Line 63: | ||
:$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | :$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | ||
| − | This result can be proved similarly to the [[Signal_Representation/The_Convolution_Theorem_and_Operation# | + | This result can be proved similarly to the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Proof_of_the_Convolution_Theorem|»convolution in the time domain«]]. However, the integration variable $\nu$ now has the dimension of a frequency. |
| − | [[File:EN_Sig_T_3_4_S2.png|right|frame|Convolution in the | + | {{GraueBox|TEXT= |
| − | + | [[File:EN_Sig_T_3_4_S2.png|right|frame|Convolution in the frequency domain $($e.g. DSB–AM$)$]] | |
| − | $\text{Example 2:}$ The [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich|Double-Sideband Amplitude Modulation]] (DSB-AM) | + | $\text{Example 2:}$ The [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich| |
| − | + | »Double-Sideband Amplitude Modulation»]] $\text{(DSB-AM)}$ with carrier suppression is described by the drawn model. | |
| − | |||
| + | *The time domain representation $\rm (blue)$ shows the modulated signal $s(t)$ as the product of the source signal $q(t)$ and the $($normalized$)$ carrier signal $z(t)$. | ||
| − | ==Convolution of a | + | |
| + | *According to the convolution theorem it follows for the frequency domain $\rm (red)$ that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ q(t)$ and $Z(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ z(t)$.}} | ||
| + | |||
| + | |||
| + | ==Convolution of a function with a Dirac delta function== | ||
<br> | <br> | ||
| − | The convolution operation becomes very simple, if one of the | + | The convolution operation becomes very simple, if one of the operands is a [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Dirac_.28delta.29_function_in_frequency_domain|»Dirac delta function«]]. This applies both to the convolution in time and frequency domain. |
| − | We will consider the convolution of a function $x_1(t)$ with the function | + | *We will consider the convolution of a function $x_1(t)$ with the function |
:$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | :$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | ||
| − | For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows: | + | *For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows: |
:$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | :$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | ||
| − | The complex exponential function leads to a shift by $T$ ⇒ [[Signal_Representation/ | + | *The complex exponential function leads to a shift by $T$ ⇒ [[Signal_Representation/Fourier_Transform_Theorems#Shifting_Theorem|»Shifting Theorem«]], the factor $\alpha$ to an attenuation $(\alpha < 1)$ or amplification $(\alpha > 1)$. From this follows: |
| − | |||
| − | From this follows: | ||
:$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | :$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{In Words: }$ The convolution of any function with a Dirac function at $t = T$ results in the function shifted to the right by $T$ while the weighting of the Dirac function by the factor $\alpha$ has to be taken into account.}} | + | $\text{In Words: }$ |
| + | *The convolution of any function with a Dirac delta function at $t = T$ results in the function shifted to the right by $T$, | ||
| + | |||
| + | *while the weighting of the Dirac delta function by the factor $\alpha$ has to be taken into account.}} | ||
| + | |||
| − | {{GraueBox|TEXT= | + | {{GraueBox|TEXT= |
| − | $\text{Example 3:}$ A | + | $\text{Example 3:}$ A rectangle pulse $x(t)$ is delayed by an LTI system by the delay time $\tau = 3\,\text{ ms}$ and attenuated by the factor $\alpha = 0.5$. |
| + | [[File:P_ID522__Sig_T_3_4_S3_neu.png|right|frame|Convolution of a rectangle pulse with a Dirac delta function]] | ||
| − | |||
| − | |||
| + | Shift and attenuation can be recognised both | ||
| + | *by the output signal $y(t)$, | ||
| + | |||
| + | *by the impulse response $h(t)$. | ||
| + | }} | ||
| − | ==Graphical | + | |
| + | ==Graphical convolution== | ||
<br> | <br> | ||
| − | + | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame|Screenshot of an older $($German$)$ version $\rm LNTwww$ applet »Convolution«:<br> $x_1(t)$ is denoted as $x(t)$ and $x_2(t)$ as $h(t)$]] | |
| − | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame|Screenshot of an older version | + | For the descriptions in this section the following convolution operation is assumed: |
| + | |||
:$$y(t) = x_1 (t) * x_2 (t) $$ | :$$y(t) = x_1 (t) * x_2 (t) $$ | ||
:$$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals. | + | The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals. |
Then the following steps are required: | Then the following steps are required: | ||
| − | # | + | # »'''Change time variables'''« of the functions: $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. |
| − | # '''Mirroring the second function''': $x_2(\tau) \to x_2(-\tau)$. | + | # »'''Mirroring the second function'''«: $x_2(\tau) \to x_2(-\tau)$. |
| − | # '''Shifting | + | # »'''Shifting the mirrorred function'''« by $t$: $x_2(-\tau) \to x_2(t-\tau)$. |
| − | # '''Multiplication''' of both functions $x_1(\tau)$ and $x_2(t-\tau)$. | + | # »'''Multiplication'''« of both functions $x_1(\tau)$ and $x_2(t-\tau)$. |
| − | # '''Integration''' over the product | + | # »'''Integration'''« over the product resp. $\tau$ between the limits $-\infty$ to $+\infty$. |
| + | |||
| + | |||
| + | <u>Note:</u> | ||
| + | *Since convolution is commutative, $x_1(\tau)$ can also be mirrored instead of $x_2(\tau)$. | ||
| − | + | *The topic is also illustrated by the HTML5 applet [[Applets:Graphical_Convolution|»Graphical Convolution«]]. | |
<br clear=all> | <br clear=all> | ||
| − | + | {{GraueBox|TEXT= | |
| + | [[File:P_ID582__Sig_T_3_4_S4_neu.png|right|frame|Jump function convoluted with the exponential function]] | ||
| + | $\text{Example 4:}$ | ||
| + | |||
| + | The procedure for the graphical convolution is now explained with a detailed example: | ||
| + | #At the input of a filter there is a jump function $x(t) = \gamma(t)$. | ||
| + | #The impulse response of the first order low-pass filter is $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$ | ||
| + | #The time axis is already renamed to $\tau$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The graphic shows | ||
| + | #the $($red colored$)$ input signal $x(\tau)$, | ||
| + | #the $($blue colored$)$ impulse response $h(\tau)$, | ||
| + | #the $($grey colored$)$ output signal $y(\tau)$. | ||
| − | |||
| − | |||
| − | The output signal can be calculated using the following equation | + | The output signal can be calculated for example using the following equation: |
:$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | Some more remarks | + | Some more remarks: |
| − | *The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$ | + | *The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$. This mirrored signal $x(-\tau)$ is multiplied by the impulse response $h(\tau)$ and integrated over it. |
| − | *As there is no time interval | + | |
| − | *For any other time $t$ the input signal must | + | *As there is no time interval, where both the blue curve $h(\tau)$ and at the same time also the red dashed mirrored curve $x(-\tau)$ is not equal to zero, the result is $y(t=0)=0$. |
| − | *As in this example | + | |
| + | *For any other time $t$ the input signal must be shifted ⇒ $x(t-\tau)$, for example according to the green dotted curve for $t=T$. | ||
| + | |||
| + | *As in this example $x(t-\tau)$ is only $0$ or $1$ the integration $($general from $\tau_1$ to $\tau_2)$ is very simple and you get here with $\tau_1 = 0$ and $\tau_2 = t$ : | ||
:$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | :$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | ||
| + | *This sketch is valid for $t=T$ and results in the output value $y(t=T) = 1 - 1/\text{e} \approx 0.632$.}} | ||
| − | |||
| + | ==Descriptive interpretation of convolution== | ||
| + | <br> | ||
| + | We assume an impulse response $h(t)$ which is first constant for one millisecond and then decreases linearly to zero until $t = 3 \,\text{ms}$. | ||
| + | [[File:P_ID524__Sig_T_3_4_S5_rah.png|right|frame|An interpretation of "Convolution"]] | ||
| + | *If $K_0 \cdot \delta(t)$ is applied to the input of this low-pass filter, the output signal $y(t)$ has the same shape as the impulse response $h(t)$. The situation is shown in red in the figure. | ||
| − | + | *The $($blue$)$ $T= 1 \,\text{ms}$ shifted Dirac delta with weight $K_1 > K_0$ results in the output signal $y_1(t)$ which is delayed with respect to the red signal and increased in amplitude. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Now we consider the input signal consisting of seven differently weighted Dirac deltas: | |
| − | |||
:$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$ | :$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$ | ||
| − | which can be understood as a time discrete approximation of a time continuous signal. | + | which can be understood as a time–discrete approximation of a time–continuous signal. |
| − | *The signal | + | *The output signal of the linear system is the sum of the seven partial signals marked with different colors in the figure: |
:$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ | :$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ | ||
| − | *We now look at the signal value at time $t = 4.5T$ (see dotted | + | *We now look at the signal value at time $t = 4.5T$ $($see dotted line$)$: |
:$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ | :$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ | ||
| − | + | *$y( {t = 4.5T} )$ is thus only determined by the input signal values $K_2$, $K_3$ and $K_4$. <u>Note:</u> | |
| − | + | ||
| − | + | #The influence of $K_4$ is the greatest due to $h(0.5T) = 1$. | |
| − | + | #The influence of $K_3$ is less strong due to $h(1.5T) = 0.75$. | |
| + | #The influence of $K_2$ is the lowest due to $h(2.5T) = 0.25$. | ||
| − | ==Proof of | + | ==Proof of the Convolution Theorem== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition: }$ | $\text{Definition: }$ | ||
| − | The following relation of time functions | + | The following relation of time functions $x_1(t)$ and $x_2(t)$ is called the »'''convolution'''« and represents this functional relation with a star: |
:$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | This results in the following Fourier correspondence: | + | *This results in the following »'''Fourier correspondence'''«: |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$}} | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$}} | ||
| Line 188: | Line 218: | ||
:$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$ | :$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$ | ||
| − | :$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$ | + | :$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t\hspace{0.05cm}'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$ |
*If you form the product of the spectral functions, you get | *If you form the product of the spectral functions, you get | ||
| Line 198: | Line 228: | ||
:$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$ | :$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$ | ||
| − | :This equation already takes into account that the exponential function is independent of the inner integration variable $τ$ | + | :This equation already takes into account that the exponential function is independent of the inner integration variable ⇒ $τ$ acts only as factor of the inner integral. |
*If we now denote the product of the two spectra with $P(f)$ and the corresponding time function with $p(t)$, the corresponding Fourier integral is | *If we now denote the product of the two spectra with $P(f)$ and the corresponding time function with $p(t)$, the corresponding Fourier integral is | ||
| Line 204: | Line 234: | ||
:$$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$ | :$$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$ | ||
| − | *A coefficient comparison of the two integrals shows that the following relationship | + | *A coefficient comparison of the last two integrals shows that the following relationship apply: |
:$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$ | :$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$ | ||
| Line 211: | Line 241: | ||
| − | ==Exercises for the | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben:Exercise_3.7: | + | [[Aufgaben:Exercise_3.7:_Synchronous_Demodulator|Exercise 3.7: Synchronous Demodulator]] |
| − | [[Aufgaben:Exercise_3.7Z: | + | [[Aufgaben:Exercise_3.7Z:_Rectangular_Signal_with_Echo|Exercise 3.7Z: Rectangular Signal with Echo]] |
| − | [[Aufgaben:Exercise_3.8:_Triple_Convolution|Exercise 3.8: Triple Convolution]] | + | [[Aufgaben:Exercise_3.8:_Triple_Convolution|Exercise 3.8: Triple Convolution?]] |
| − | [[Aufgaben:Exercise_3.8Z:Convolution_of_Two_Rectangles|Exercise 3.8Z:Convolution of Two Rectangles]] | + | [[Aufgaben:Exercise_3.8Z:Convolution_of_Two_Rectangles|Exercise 3.8Z: Convolution of Two Rectangles]] |
[[Aufgaben:Exercise_3.9:_Convolution_of_Rectangle_and_Gaussian_Pulse|Exercise 3.9: Convolution of Rectangle and Gaussian Pulse]] | [[Aufgaben:Exercise_3.9:_Convolution_of_Rectangle_and_Gaussian_Pulse|Exercise 3.9: Convolution of Rectangle and Gaussian Pulse]] | ||
Latest revision as of 16:50, 15 June 2023
Contents
Convolution in the time domain
The »Convolution Theorem« is one of the most important laws of the Fourier transform, to which an own subchapter is dedicated in this tutorial. We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known:
- $$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
$\tau$ is a formal integration variable with the dimension of a time.
$\text{Definition:}$
The above connection of the time function $x_1(t)$ and $x_2(t)$ is called »convolution«. One represents this functional connection with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$
- Thus the above Fourier correspondence can be written as follows:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
- The convolution is »commutative« ⇒ The order of the operands can be changed:
- $$x_1(t) * x_2(t) =x_2(t) * x_1(t).$$
- The »Proof« will be shown at the end of this chapter.
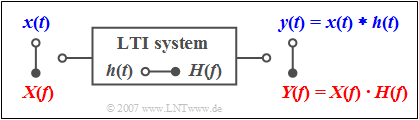
$\text{Example 1:}$ Every linear time-invariant $\rm (LTI)$ system can be described both,
- by the frequency response $H(f)$,
- by the impulse response $h(t)$.
The relation between these two system quantities is also given by the Fourier transform.
- If the signal $x(t)$ with spectrum $X(f)$ is applied to the input, then the spectrum of the output signal is:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
- It is possible to calculate the output signal in the time domain with the convolution theorem:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
- This equation shows again the »commutativity« of the »convolution operation«.
Convolution in the frequency domain
The duality between time and frequency domain also allows statements regarding the spectrum of the product signal:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
This result can be proved similarly to the »convolution in the time domain«. However, the integration variable $\nu$ now has the dimension of a frequency.
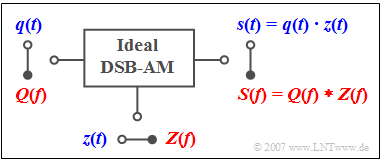
$\text{Example 2:}$ The »Double-Sideband Amplitude Modulation» $\text{(DSB-AM)}$ with carrier suppression is described by the drawn model.
- The time domain representation $\rm (blue)$ shows the modulated signal $s(t)$ as the product of the source signal $q(t)$ and the $($normalized$)$ carrier signal $z(t)$.
- According to the convolution theorem it follows for the frequency domain $\rm (red)$ that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ q(t)$ and $Z(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ z(t)$.
Convolution of a function with a Dirac delta function
The convolution operation becomes very simple, if one of the operands is a »Dirac delta function«. This applies both to the convolution in time and frequency domain.
- We will consider the convolution of a function $x_1(t)$ with the function
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
- For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
- The complex exponential function leads to a shift by $T$ ⇒ »Shifting Theorem«, the factor $\alpha$ to an attenuation $(\alpha < 1)$ or amplification $(\alpha > 1)$. From this follows:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In Words: }$
- The convolution of any function with a Dirac delta function at $t = T$ results in the function shifted to the right by $T$,
- while the weighting of the Dirac delta function by the factor $\alpha$ has to be taken into account.
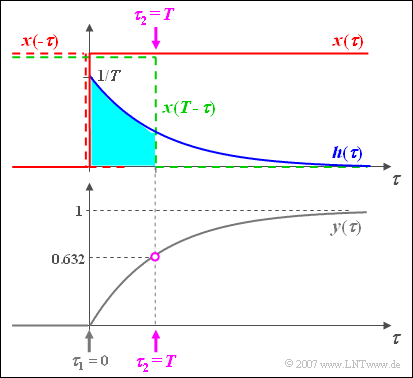
$\text{Example 3:}$ A rectangle pulse $x(t)$ is delayed by an LTI system by the delay time $\tau = 3\,\text{ ms}$ and attenuated by the factor $\alpha = 0.5$.
Shift and attenuation can be recognised both
- by the output signal $y(t)$,
- by the impulse response $h(t)$.
Graphical convolution
For the descriptions in this section the following convolution operation is assumed:
- $$y(t) = x_1 (t) * x_2 (t) $$
- $$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals.
Then the following steps are required:
- »Change time variables« of the functions: $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$.
- »Mirroring the second function«: $x_2(\tau) \to x_2(-\tau)$.
- »Shifting the mirrorred function« by $t$: $x_2(-\tau) \to x_2(t-\tau)$.
- »Multiplication« of both functions $x_1(\tau)$ and $x_2(t-\tau)$.
- »Integration« over the product resp. $\tau$ between the limits $-\infty$ to $+\infty$.
Note:
- Since convolution is commutative, $x_1(\tau)$ can also be mirrored instead of $x_2(\tau)$.
- The topic is also illustrated by the HTML5 applet »Graphical Convolution«.
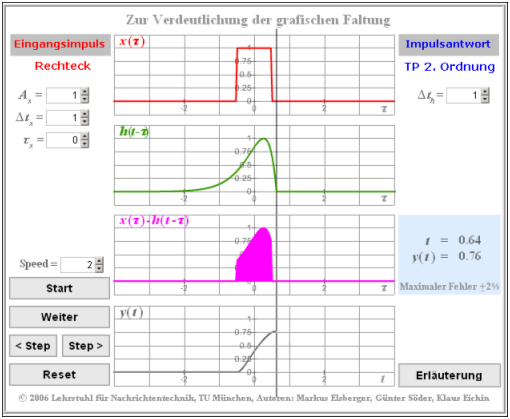
$\text{Example 4:}$
The procedure for the graphical convolution is now explained with a detailed example:
- At the input of a filter there is a jump function $x(t) = \gamma(t)$.
- The impulse response of the first order low-pass filter is $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$
- The time axis is already renamed to $\tau$.
The graphic shows
- the $($red colored$)$ input signal $x(\tau)$,
- the $($blue colored$)$ impulse response $h(\tau)$,
- the $($grey colored$)$ output signal $y(\tau)$.
The output signal can be calculated for example using the following equation:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Some more remarks:
- The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$. This mirrored signal $x(-\tau)$ is multiplied by the impulse response $h(\tau)$ and integrated over it.
- As there is no time interval, where both the blue curve $h(\tau)$ and at the same time also the red dashed mirrored curve $x(-\tau)$ is not equal to zero, the result is $y(t=0)=0$.
- For any other time $t$ the input signal must be shifted ⇒ $x(t-\tau)$, for example according to the green dotted curve for $t=T$.
- As in this example $x(t-\tau)$ is only $0$ or $1$ the integration $($general from $\tau_1$ to $\tau_2)$ is very simple and you get here with $\tau_1 = 0$ and $\tau_2 = t$ :
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
- This sketch is valid for $t=T$ and results in the output value $y(t=T) = 1 - 1/\text{e} \approx 0.632$.
Descriptive interpretation of convolution
We assume an impulse response $h(t)$ which is first constant for one millisecond and then decreases linearly to zero until $t = 3 \,\text{ms}$.
- If $K_0 \cdot \delta(t)$ is applied to the input of this low-pass filter, the output signal $y(t)$ has the same shape as the impulse response $h(t)$. The situation is shown in red in the figure.
- The $($blue$)$ $T= 1 \,\text{ms}$ shifted Dirac delta with weight $K_1 > K_0$ results in the output signal $y_1(t)$ which is delayed with respect to the red signal and increased in amplitude.
Now we consider the input signal consisting of seven differently weighted Dirac deltas:
- $$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$
which can be understood as a time–discrete approximation of a time–continuous signal.
- The output signal of the linear system is the sum of the seven partial signals marked with different colors in the figure:
- $$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$
- We now look at the signal value at time $t = 4.5T$ $($see dotted line$)$:
- $$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$
- $y( {t = 4.5T} )$ is thus only determined by the input signal values $K_2$, $K_3$ and $K_4$. Note:
- The influence of $K_4$ is the greatest due to $h(0.5T) = 1$.
- The influence of $K_3$ is less strong due to $h(1.5T) = 0.75$.
- The influence of $K_2$ is the lowest due to $h(2.5T) = 0.25$.
Proof of the Convolution Theorem
$\text{Definition: }$ The following relation of time functions $x_1(t)$ and $x_2(t)$ is called the »convolution« and represents this functional relation with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- This results in the following »Fourier correspondence«:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
$\text{Proof: }$ The Fourier integrals of functions $x_1(t)$ and $x_2(t)$ are with modified integration variables:
- $$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$
- $$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t\hspace{0.05cm}'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$
- If you form the product of the spectral functions, you get
- $$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$
- With the substitution $t = \tau + t\hspace{0.05cm}'$ results:
- $$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$
- This equation already takes into account that the exponential function is independent of the inner integration variable ⇒ $τ$ acts only as factor of the inner integral.
- If we now denote the product of the two spectra with $P(f)$ and the corresponding time function with $p(t)$, the corresponding Fourier integral is
- $$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$
- A coefficient comparison of the last two integrals shows that the following relationship apply:
- $$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$
Exercises for the chapter
Exercise 3.7: Synchronous Demodulator
Exercise 3.7Z: Rectangular Signal with Echo
Exercise 3.8: Triple Convolution?
Exercise 3.8Z: Convolution of Two Rectangles
Exercise 3.9: Convolution of Rectangle and Gaussian Pulse
Exercise 3.9Z: Convolution of Gaussian Pulses