Difference between revisions of "Aufgaben:Exercise 2.11Z: Arithmetic Coding once again"
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Further_Source_Coding_Methods |
}} | }} | ||
[[File:EN_Inf_Z_2_11_v2.png|right|frame|Preset interval ranges]] | [[File:EN_Inf_Z_2_11_v2.png|right|frame|Preset interval ranges]] | ||
| − | Here we consider arithmetic coding $(\rm AC)$. All necessary information about this type of entropy coding can be found in [[Aufgaben: | + | Here we consider arithmetic coding $(\rm AC)$. All necessary information about this type of entropy coding can be found in [[Aufgaben:Exercise_2.11:_Arithmetic_Coding|Exercise 2.11]]. |
The graph is also the result of Exercise 2.11. The numerical values for coding steps 3 and 7 that are important for the current task are highlighted in colour: | The graph is also the result of Exercise 2.11. The numerical values for coding steps 3 and 7 that are important for the current task are highlighted in colour: | ||
| Line 13: | Line 13: | ||
This task is only about assigning binary sequences to the selected intervals. Procedure: | This task is only about assigning binary sequences to the selected intervals. Procedure: | ||
| − | * The interval $I$ is determined by the beginning $B$, the end $E$, the interval width ${\it \Delta} = E-B$ | + | * The interval $I$ is determined by the beginning $B$, the end $E$, the interval width ${\it \Delta} = E-B$ as well as the interval centre $M = (B+E)/2$. |
| − | * The interval $I$ is characterised by the binary representation (with limited resolution) of any real number value $r \in I$. For example, one chooses $r \approx M$. | + | * The interval $I$ is characterised by the binary representation (with limited resolution) of any real number value $r \in I$. For example, one chooses $r \approx M$. |
| − | * The required number of bits results from the interval width according to the following equation (the open square brackets mean "round up"): | + | * The required number of bits results from the interval width according to the following equation (the open square brackets mean "round up"): |
| − | :$$N_{\rm | + | :$$N_{\rm bits} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$ |
| − | For example, for $N_{\rm | + | For example, for $N_{\rm bits} = 5$ the binary code <b>01001</b> stands for the following real-valued number $r$: |
:$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 | :$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| Line 28: | Line 28: | ||
| − | Hints: | + | <u>Hints:</u> |
| − | *The | + | *The exercise belongs to the chapter [[Information_Theory/Further_Source_Coding_Methods|Further source coding methods]]. |
| − | *In particular, reference is made to the page [[Information_Theory/ | + | *In particular, reference is made to the page [[Information_Theory/Further_Source_Coding_Methods#Arithmetic_coding|Arithmetic Coding]]. |
*Further information on the topic can also be found in this [https://en.wikipedia.org/wiki/Arithmetic_coding Wikipedia article]. | *Further information on the topic can also be found in this [https://en.wikipedia.org/wiki/Arithmetic_coding Wikipedia article]. | ||
| Line 40: | Line 40: | ||
{How many bits are used to represent the source symbol sequence $\rm XXY$ ⇒ $N = 3$ ? | {How many bits are used to represent the source symbol sequence $\rm XXY$ ⇒ $N = 3$ ? | ||
|type="{}"} | |type="{}"} | ||
| − | $N_\text{ | + | $N_\text{bits} \ = \ $ { 6 } |
| Line 52: | Line 52: | ||
{How many bits are used to represent the source symbol sequence $\rm XXYXXXZ$ ⇒ $N = 7$ ? | {How many bits are used to represent the source symbol sequence $\rm XXYXXXZ$ ⇒ $N = 7$ ? | ||
|type="{}"} | |type="{}"} | ||
| − | $N_\text{ | + | $N_\text{bits} \ = \ $ { 11 } |
| Line 64: | Line 64: | ||
|type="[]"} | |type="[]"} | ||
+ It is a common coding of entire sequences. | + It is a common coding of entire sequences. | ||
| − | + A 32 | + | + A computer with 32-bit architecture limits the sequence length $N$. |
+ This problem can be circumvented by integer realisation. | + This problem can be circumvented by integer realisation. | ||
+ Integer realisation increases the coding speed. | + Integer realisation increases the coding speed. | ||
| Line 74: | Line 74: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The selected interval begins at $B_3 = 0.343$ and ends at $E_3 = 0.392$. |
| − | * | + | *The interval width is therefore ${\it \Delta}_3 = 0.049$ and thus the following applies with the logarithm to base 2: |
| − | :$$N_{\rm | + | :$$N_{\rm bits} = {\rm log_2} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The selected interval results in $I = \big[0.343, \ 0.392\big)$. |
| − | * | + | *The middle lies at $M_3 = 0.3675$. |
| − | * | + | *To determine the arithmetic code, we try to reach the centre of the interval as well as possible by using a binary representation. |
| − | * | + | *Since we do not have a corresponding tool for solving this task at the moment, we assume the following secondary calculations: |
| − | |||
| − | : $ | + | : $H_4 = 2^{-2} + 2^{-4} = 0.3125$ ⇒ does not belong to interval $I$. |
| − | : $ | + | : $H_5 = H_4 +2^{-5} = 0.34375 \in I$ ⇒ binary representation: '''0.01011''' ⇒ Code: <b>01011</b>. |
| − | : $ | + | : $H_6 = H_5 +2^{-6} = 0.359375 \in I$ ⇒ binary representation: '''0.010111''' ⇒ Code: <b>010111</b>. |
| − | : $ | + | : $H_7 = H_6 +2^{-7} = 0.3671875 \in I$ ⇒ binary representation: '''0.0101111''' ⇒ Code: <b>0101111</b>. |
| − | + | : $H_{12} = H_7 +2^{-12} = 0.3674316406 \in I$ ⇒ binary representation: '''0.010111100001''' ⇒ Code: <b>010111100001</b>. | |
| + | The corresponding 6–bit code is therefore $\rm AC =$ <b>010111</b> ⇒ Correct is <u>solution suggestion 2</u>. | ||
| − | '''(3)''' | + | |
| − | :$$N_{\rm | + | '''(3)''' Here, with the beginning $B_7 = 0.3564456$ and the end $E_7 = 0.359807$ the interval width is ${\it \Delta}_7 = 0.0033614$ and thus |
| + | :$$N_{\rm bits} = \left\lceil {\rm log_2} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = | ||
\left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} | \left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 107: | Line 108: | ||
| − | '''(4)''' | + | '''(4)''' The binary representation of the code <b>01011100001</b> results in |
:$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 | :$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The correct answer is therefore <u>NO</u>. The valid arithmetic code is $\rm AC =$ <b>01011011101</b>, because of |
:$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} | :$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$ | \Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$ | ||
| − | '''(5)''' <u> | + | '''(5)''' <u>All statements</u> are correct. See also [https://en.wikipedia.org/wiki/Arithmetic_coding '''this Wikipedia article''']. |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:26, 12 August 2021
Here we consider arithmetic coding $(\rm AC)$. All necessary information about this type of entropy coding can be found in Exercise 2.11.
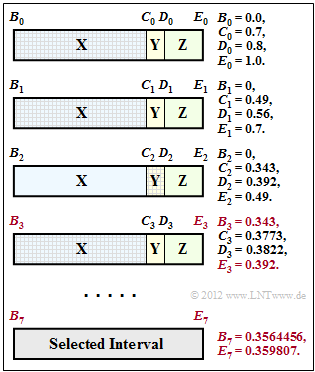
The graph is also the result of Exercise 2.11. The numerical values for coding steps 3 and 7 that are important for the current task are highlighted in colour:
- The interval for $N= 3$ $($symbol sequence $\rm XXY)$ starts at $B_3 = 0.343$ and goes up to $E_3 = 0.392$.
- The interval limits for $N= 7$ $($symbol sequence $\rm XXYXXXZ)$ are $B_7 = 0.3564456$ and $E_7 =0.359807$.
This task is only about assigning binary sequences to the selected intervals. Procedure:
- The interval $I$ is determined by the beginning $B$, the end $E$, the interval width ${\it \Delta} = E-B$ as well as the interval centre $M = (B+E)/2$.
- The interval $I$ is characterised by the binary representation (with limited resolution) of any real number value $r \in I$. For example, one chooses $r \approx M$.
- The required number of bits results from the interval width according to the following equation (the open square brackets mean "round up"):
- $$N_{\rm bits} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$
For example, for $N_{\rm bits} = 5$ the binary code 01001 stands for the following real-valued number $r$:
- $$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 \hspace{0.05cm}. $$
Hints:
- The exercise belongs to the chapter Further source coding methods.
- In particular, reference is made to the page Arithmetic Coding.
- Further information on the topic can also be found in this Wikipedia article.
Questions
Solution
- The interval width is therefore ${\it \Delta}_3 = 0.049$ and thus the following applies with the logarithm to base 2:
- $$N_{\rm bits} = {\rm log_2} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} \hspace{0.05cm}.$$
(2) The selected interval results in $I = \big[0.343, \ 0.392\big)$.
- The middle lies at $M_3 = 0.3675$.
- To determine the arithmetic code, we try to reach the centre of the interval as well as possible by using a binary representation.
- Since we do not have a corresponding tool for solving this task at the moment, we assume the following secondary calculations:
- $H_4 = 2^{-2} + 2^{-4} = 0.3125$ ⇒ does not belong to interval $I$.
- $H_5 = H_4 +2^{-5} = 0.34375 \in I$ ⇒ binary representation: 0.01011 ⇒ Code: 01011.
- $H_6 = H_5 +2^{-6} = 0.359375 \in I$ ⇒ binary representation: 0.010111 ⇒ Code: 010111.
- $H_7 = H_6 +2^{-7} = 0.3671875 \in I$ ⇒ binary representation: 0.0101111 ⇒ Code: 0101111.
- $H_{12} = H_7 +2^{-12} = 0.3674316406 \in I$ ⇒ binary representation: 0.010111100001 ⇒ Code: 010111100001.
The corresponding 6–bit code is therefore $\rm AC =$ 010111 ⇒ Correct is solution suggestion 2.
(3) Here, with the beginning $B_7 = 0.3564456$ and the end $E_7 = 0.359807$ the interval width is ${\it \Delta}_7 = 0.0033614$ and thus
- $$N_{\rm bits} = \left\lceil {\rm log_2} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} \hspace{0.05cm}.$$
(4) The binary representation of the code 01011100001 results in
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 \hspace{0.05cm}.$$
- The correct answer is therefore NO. The valid arithmetic code is $\rm AC =$ 01011011101, because of
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$
(5) All statements are correct. See also this Wikipedia article.