Difference between revisions of "Aufgaben:Exercise 2.2Z: Average Code Word Length"
| (2 intermediate revisions by one other user not shown) | |||
| Line 6: | Line 6: | ||
The aim of data compression is to represent the message of a source with as few binary characters as possible. | The aim of data compression is to represent the message of a source with as few binary characters as possible. | ||
| − | We consider here a discrete | + | We consider here a discrete message source with the symbol set $\rm \{ A, \ B, \ C, \ D\}$ ⇒ symbol set size $M = 4$ and the symbol probabilities |
:*$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ $($subtask $1)$, | :*$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ $($subtask $1)$, | ||
:* $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ $($subtask $2$ to $5)$. | :* $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ $($subtask $2$ to $5)$. | ||
| Line 18: | Line 18: | ||
| − | A measure for the quality of a compression method is the average | + | A measure for the quality of a compression method is the average code word length $L_{\rm M}$ with the additional unit "bit/source symbol". |
| Line 37: | Line 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Determine the average | + | {Determine the average code word length $L_{\rm M}$ for $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$. |
|type="{}"} | |type="{}"} | ||
$\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/source\hspace{0.15cm} symbol$ | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/source\hspace{0.15cm} symbol$ | ||
| Line 53: | Line 53: | ||
{How can you recognise prefix-free codes? | {How can you recognise prefix-free codes? | ||
|type="[]"} | |type="[]"} | ||
| − | + No | + | + No code word is the beginning of another code word. |
| − | - All | + | - All code words have the same length. |
| − | {For the special source symbol sequence $\rm ADBDCBCBADCA$ , the | + | {For the special source symbol sequence $\rm ADBDCBCBADCA$ , the encoded sequence $\rm 001101111001100100111000$ results. |
<br>Which code was used? | <br>Which code was used? | ||
|type="()"} | |type="()"} | ||
| Line 75: | Line 75: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The average | + | '''(1)''' The average code word length is generally given by |
:$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | :$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 87: | Line 87: | ||
| − | '''(2)''' With the code table $\text{C1}$ , the average | + | '''(2)''' With the code table $\text{C1}$ , the average code word length $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \rm bit/source\hspace{0.15cm} symbol$ is always obtained, independent of the symbol probabilities. |
For the other two codes one obtains: | For the other two codes one obtains: | ||
| Line 96: | Line 96: | ||
From the example you can see the principle: | From the example you can see the principle: | ||
*Probable symbols are represented by a few binary symbols, improbable ones by more. | *Probable symbols are represented by a few binary symbols, improbable ones by more. | ||
| − | *In the case of equally probable symbols, it is best to choose the same | + | *In the case of equally probable symbols, it is best to choose the same code word lengths. |
| Line 102: | Line 102: | ||
'''(3)''' <u>Solution suggestion 1</u> is correct: | '''(3)''' <u>Solution suggestion 1</u> is correct: | ||
| − | *The code $\text{C1}$ with uniform length of all | + | *The code $\text{C1}$ with uniform length of all code words is prefix-free, |
*but other codes can also be prefix-free, for example the codes $\text{C2}$ and $\text{C3}$. | *but other codes can also be prefix-free, for example the codes $\text{C2}$ and $\text{C3}$. | ||
| Line 115: | Line 115: | ||
'''(5)''' <u>Solution suggestion 2</u> is correct. | '''(5)''' <u>Solution suggestion 2</u> is correct. | ||
| − | The first suggested solution gives the source symbol sequence for code $\text{C2}$ if the | + | The first suggested solution gives the source symbol sequence for code $\text{C2}$ if the encoded sequence would be "$\rm 001101111001100100111000$". |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:53, 1 November 2022
The aim of data compression is to represent the message of a source with as few binary characters as possible.
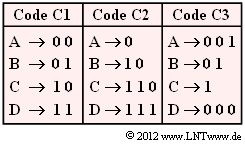
We consider here a discrete message source with the symbol set $\rm \{ A, \ B, \ C, \ D\}$ ⇒ symbol set size $M = 4$ and the symbol probabilities
- $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ $($subtask $1)$,
- $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ $($subtask $2$ to $5)$.
It is assumed that there are no statistical Dependencies between the individual source symbols.
Three assignments are given. To be noted:
- Each of these binary codes $\rm C1$, $\rm C2$ and $\rm C3$ is designed for a specific source statistic.
- All codes are prefix-free and thus immediately decodable without further specification.
A measure for the quality of a compression method is the average code word length $L_{\rm M}$ with the additional unit "bit/source symbol".
Hint:
- The exercise belongs to the chapter General Description of Source Coding.
Questions
Solution
- $$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$
If the four source symbols are equally probable $($all probabilities exactly $1/4)$, then for this we can also write:
- $$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) \hspace{0.05cm}.$$
- $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/source\hspace{0.15cm} symbol$,
- $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source\hspace{0.15cm} symbol$
- $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/source\hspace{0.15cm} symbol$.
(2) With the code table $\text{C1}$ , the average code word length $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \rm bit/source\hspace{0.15cm} symbol$ is always obtained, independent of the symbol probabilities.
For the other two codes one obtains:
- $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/source\hspace{0.15cm} symbol$,
- $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/source\hspace{0.15cm} symbol$.
From the example you can see the principle:
- Probable symbols are represented by a few binary symbols, improbable ones by more.
- In the case of equally probable symbols, it is best to choose the same code word lengths.
(3) Solution suggestion 1 is correct:
- The code $\text{C1}$ with uniform length of all code words is prefix-free,
- but other codes can also be prefix-free, for example the codes $\text{C2}$ and $\text{C3}$.
(4) Solution suggestion 1 is correct:
- Already from "00" at the beginning one can see that the code $\text{C2}$ is out of the question here,
because otherwise the source symbol sequence would have to begin with "AA". - In fact, the code $\text{C1}$ was used.
(5) Solution suggestion 2 is correct.
The first suggested solution gives the source symbol sequence for code $\text{C2}$ if the encoded sequence would be "$\rm 001101111001100100111000$".