Difference between revisions of "Aufgaben:Exercise 3.2Z: Two-dimensional Probability Mass Function"
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables |
}} | }} | ||
| Line 22: | Line 22: | ||
| − | Hints: | + | <u>Hints:</u> |
*The exercise belongs to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Some preliminary remarks on two-dimensional random variables]]. | *The exercise belongs to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Some preliminary remarks on two-dimensional random variables]]. | ||
*The same constellation is assumed here as in [[Aufgaben:Aufgabe_3.2:_Erwartungswertberechnungen|Exercise 3.2]]. | *The same constellation is assumed here as in [[Aufgaben:Aufgabe_3.2:_Erwartungswertberechnungen|Exercise 3.2]]. | ||
| Line 72: | Line 72: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' You get from $P_{XY}(X,\ Y)$ to the | + | '''(1)''' You get from $P_{XY}(X,\ Y)$ to the one-dimensional probability mass function $P_X(X)$ by summing up all $Y$ probabilities: |
:$$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$ | :$$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$ | ||
*One thus obtains the following numerical values: | *One thus obtains the following numerical values: | ||
| Line 91: | Line 91: | ||
'''(3)''' With statistical independence, $P_{XY}(X,Y)= P_X(X) \cdot P_Y(Y)$ should be. | '''(3)''' With statistical independence, $P_{XY}(X,Y)= P_X(X) \cdot P_Y(Y)$ should be. | ||
| − | *This does not apply here: answer <u>''' | + | *This does not apply here: answer <u>'''NO'''</u>. |
| − | '''(4)''' Starting from the left-hand table ⇒ $P_{XY}(X,Y)$ | + | '''(4)''' Starting from the left-hand table ⇒ $P_{XY}(X,Y)$, we arrive at the middle table ⇒ $P_{UY}(U,Y)$, <br>by combining certain probabilities according to $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$. |
| + | If one also takes into account $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$, one obtains the probabilities sought according to the right-hand table: | ||
[[File:P_ID2753__Inf_Z_3_2d_neu.png|right|frame|Different probability functions]] | [[File:P_ID2753__Inf_Z_3_2d_neu.png|right|frame|Different probability functions]] | ||
| − | |||
:$$P_{UV}( U = 0, V = 0) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | :$$P_{UV}( U = 0, V = 0) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | ||
:$$P_{UV}( U = 0, V = 1) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | :$$P_{UV}( U = 0, V = 1) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$ | ||
| Line 107: | Line 107: | ||
| − | '''(5)''' The correct answer is <u>''' | + | '''(5)''' The correct answer is <u>'''YES'''</u>: |
| − | *The corresponding | + | *The corresponding one-dimensional probability mass functions are: |
:$$P_U(U) = \big [1/2 , \ 1/2 \big ],$$ | :$$P_U(U) = \big [1/2 , \ 1/2 \big ],$$ | ||
:$$P_V(V)=\big [3/4, \ 1/4 \big ].$$ | :$$P_V(V)=\big [3/4, \ 1/4 \big ].$$ | ||
Latest revision as of 09:12, 24 September 2021
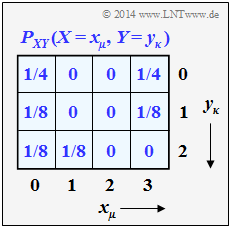
We consider the random variables $X = \{ 0,\ 1,\ 2,\ 3 \}$ and $Y = \{ 0,\ 1,\ 2 \}$, whose joint probability mass function $P_{XY}(X,\ Y)$ is given.
- From this two-dimensional probability mass function $\rm (PMF)$, the one-dimensional probability mass functions $P_X(X)$ and $P_Y(Y)$ are to be determined.
- Such a one-dimensional probability mass function is sometimes also called "marginal probability".
If $P_{XY}(X,\ Y) = P_X(X) \cdot P_Y(Y)$, the two random variables $X$ and $Y$ are statistically independent. Otherwise, there are statistical dependencies between them.
In the second part of the task we consider the random variables $U= \big \{ 0,\ 1 \big \}$ and $V= \big \{ 0,\ 1 \big \}$, which result from $X$ and $Y$ by modulo-2 operations:
- $$U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2, \hspace{0.3cm} V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2.$$
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- The same constellation is assumed here as in Exercise 3.2.
- There the random variables $Y = \{ 0,\ 1,\ 2,\ 3 \}$ were considered, but with the addition ${\rm Pr}(Y = 3) = 0$.
- The property $|X| = |Y|$ forced in this way was advantageous in the previous task for the formal calculation of the expected value.
Questions
Solution
- $$P_X(X = x_{\mu}) = \sum_{y \hspace{0.05cm} \in \hspace{0.05cm} Y} \hspace{0.1cm} P_{XY}(x_{\mu}, y).$$
- One thus obtains the following numerical values:
- $$P_X(X = 0) = 1/4+1/8+1/8 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$
- $$P_X(X = 1)= 0+0+1/8 = 1/8 \hspace{0.15cm}\underline{= 0.125},$$
- $$P_X(X = 2) = 0+0+0 \hspace{0.15cm}\underline{= 0}$$
- $$P_X(X = 3) = 1/4+1/8+0=3/8 \hspace{0.15cm}\underline{= 0.375}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} P_X(X) = \big [ 1/2, \ 1/8 , \ 0 , \ 3/8 \big ].$$
(2) Analogous to sub-task (1) , the following now holds:
- $$P_Y(Y = y_{\kappa}) = \sum_{x \hspace{0.05cm} \in \hspace{0.05cm} X} \hspace{0.1cm} P_{XY}(x, y_{\kappa})$$
- $$P_Y(Y= 0) = 1/4+0+0+1/4 = 1/2 \hspace{0.15cm}\underline{= 0.500},$$
- $$P_Y(Y = 1) = 1/8+0+0+1/8 = 1/4 \hspace{0.15cm}\underline{= 0.250},$$
- $$P_Y(Y = 2) = 1/8+1/8+0+0 = 1/4 \hspace{0.15cm}\underline{= 0.250} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} P_Y(Y= 0) = \big [ 1/2, \ 1/4 , \ 1/4 ].$$
(3) With statistical independence, $P_{XY}(X,Y)= P_X(X) \cdot P_Y(Y)$ should be.
- This does not apply here: answer NO.
(4) Starting from the left-hand table ⇒ $P_{XY}(X,Y)$, we arrive at the middle table ⇒ $P_{UY}(U,Y)$,
by combining certain probabilities according to $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$.
If one also takes into account $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$, one obtains the probabilities sought according to the right-hand table:
- $$P_{UV}( U = 0, V = 0) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$
- $$P_{UV}( U = 0, V = 1) = 3/8 \hspace{0.15cm}\underline{= 0.375},$$
- $$P_{UV}( U = 1, V = 0) = 1/8 \hspace{0.15cm}\underline{= 0.125},$$
- $$P_{UV}( U = 1, V = 1) = 1/8 \hspace{0.15cm}\underline{= 0.125}.$$
(5) The correct answer is YES:
- The corresponding one-dimensional probability mass functions are:
- $$P_U(U) = \big [1/2 , \ 1/2 \big ],$$
- $$P_V(V)=\big [3/4, \ 1/4 \big ].$$
- Thus: $P_{UV}(U,V) = P_U(U) \cdot P_V(V)$ ⇒ $U$ and $V$ are statistically independent.