Difference between revisions of "Aufgaben:Exercise 3.7: Some Entropy Calculations"
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables |
}} | }} | ||
| Line 8: | Line 8: | ||
:$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$ | :$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$ | ||
| − | For the random variable $XY$ the following are to be calculated in this | + | For the random variable $XY$ the following are to be calculated in this exercise: |
* the joint entropy: | * the joint entropy: | ||
:$$H(XY) = -{\rm E}\big [\log_2 P_{ XY }( X,Y) \big ],$$ | :$$H(XY) = -{\rm E}\big [\log_2 P_{ XY }( X,Y) \big ],$$ | ||
| Line 31: | Line 31: | ||
Hints: | Hints: | ||
| − | *The exercise belongs to the chapter [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables|Different | + | *The exercise belongs to the chapter [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables|Different entropy measures of two-dimensional random variables]]. |
*In particular, reference is made to the pages <br> [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables#Conditional_probability_and_conditional_entropy|Conditional probability and conditional entropy]] as well as <br> [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables#Mutual_information_between_two_random_variables|Mutual information between two random variables]]. | *In particular, reference is made to the pages <br> [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables#Conditional_probability_and_conditional_entropy|Conditional probability and conditional entropy]] as well as <br> [[Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables#Mutual_information_between_two_random_variables|Mutual information between two random variables]]. | ||
| Line 43: | Line 43: | ||
$H(XY) \ = \ $ { 1.393 3% } $\ \rm bit$ | $H(XY) \ = \ $ { 1.393 3% } $\ \rm bit$ | ||
| − | {What are the entropies of the | + | {What are the entropies of the one-dimensional random variables $X$ and $Y$ ? |
|type="{}"} | |type="{}"} | ||
$H(X) \ = \ $ { 0.722 3% } $\ \rm bit$ | $H(X) \ = \ $ { 0.722 3% } $\ \rm bit$ | ||
$H(Y) \ = \ $ { 0.925 3% } $\ \rm bit$ | $H(Y) \ = \ $ { 0.925 3% } $\ \rm bit$ | ||
| − | {How large is the | + | {How large is the mutual information between the random variables $X$ and $Y$? |
|type="{}"} | |type="{}"} | ||
$I(X; Y) \ = \ $ { 0.254 3% } $\ \rm bit$ | $I(X; Y) \ = \ $ { 0.254 3% } $\ \rm bit$ | ||
| Line 58: | Line 58: | ||
| − | {Which of the following statements are true for the | + | {Which of the following statements are true for the two-dimensional random variable $UV$? |
|type="[]"} | |type="[]"} | ||
| − | + The | + | + The one-dimensional random variables $U$ and $V$ are statistically independent. |
+ The mutual information of $U$ and $V$ is $I(U; V) = 0$. | + The mutual information of $U$ and $V$ is $I(U; V) = 0$. | ||
- For the compound entropy $H(UV) = H(XY)$ holds. | - For the compound entropy $H(UV) = H(XY)$ holds. | ||
| Line 81: | Line 81: | ||
| − | '''(2)''' The | + | '''(2)''' The one-dimensional probability functions are $P_X(X) = \big [0.2, \ 0.8 \big ]$ and $P_Y(Y) = \big [0.34, \ 0.66 \big ]$. From this follows: |
:$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.8\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.8}\hspace{0.15cm} \underline {= 0.722\,{\rm (bit)}} \hspace{0.05cm},$$ | :$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.8\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.8}\hspace{0.15cm} \underline {= 0.722\,{\rm (bit)}} \hspace{0.05cm},$$ | ||
:$$H(Y) =0.34 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.34} + 0.66\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.66}\hspace{0.15cm} \underline {= 0.925\,{\rm (bit)}} \hspace{0.05cm}.$$ | :$$H(Y) =0.34 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.34} + 0.66\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.66}\hspace{0.15cm} \underline {= 0.925\,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| Line 98: | Line 98: | ||
[[File:P_ID2767__Inf_A_3_6d.png|right|frame|Entropy values for the random variables $XY$ and $UV$]] | [[File:P_ID2767__Inf_A_3_6d.png|right|frame|Entropy values for the random variables $XY$ and $UV$]] | ||
| − | *The | + | *The left diagram summarises the results of subtasks '''(1)''', ... , '''(4)''' true to scale. |
*The joint entropy is highlighted in grey and the mutual information in yellow. | *The joint entropy is highlighted in grey and the mutual information in yellow. | ||
| − | *A red background refers to the random variable $X$, a green one to $Y$. Hatched fields indicate conditional entropy. | + | *A red background refers to the random variable $X$, and a green one to $Y$. Hatched fields indicate a conditional entropy. |
| Line 106: | Line 106: | ||
| − | '''(5)''' According to the diagram, statements 1, 2 and 4 are correct: | + | '''(5)''' According to the diagram on the right, <br>statements 1, 2 and 4 are correct: |
*One recognises the validity of $P_{ UV } = P_U · P_V$ ⇒ mutual information $I(U; V) = 0$ by the fact that the second row of the $P_{ UV }$ matrix differs from the first row only by a constant factor $(4)$ . | *One recognises the validity of $P_{ UV } = P_U · P_V$ ⇒ mutual information $I(U; V) = 0$ by the fact that the second row of the $P_{ UV }$ matrix differs from the first row only by a constant factor $(4)$ . | ||
| − | *This results in the same | + | *This results in the same one-dimensional probability mass functions as for the random variable $XY$ ⇒ $P_U(U) = \big [0.2, \ 0.8 \big ]$ and $P_V(V) = \big [0.34, \ 0.66 \big ]$. |
| − | *Therefore $H(U) = H(X) = 0.722\ \rm bit$ | + | *Therefore $H(U) = H(X) = 0.722\ \rm bit$ and $H(V) = H(Y) = 0.925 \ \rm bit$. |
*Here, however, the following now applies for the joint entropy: $H(UV) = H(U) + H(V) ≠ H(XY)$. | *Here, however, the following now applies for the joint entropy: $H(UV) = H(U) + H(V) ≠ H(XY)$. | ||
Latest revision as of 09:15, 24 September 2021
We consider the two random variables $XY$ and $UV$ with the following two-dimensional probability mass functions:
- $$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$
- $$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$
For the random variable $XY$ the following are to be calculated in this exercise:
- the joint entropy:
- $$H(XY) = -{\rm E}\big [\log_2 P_{ XY }( X,Y) \big ],$$
- the two individual entropies:
- $$H(X) = -{\rm E}\big [\log_2 P_X( X)\big ],$$
- $$H(Y) = -{\rm E}\big [\log_2 P_Y( Y)\big ].$$
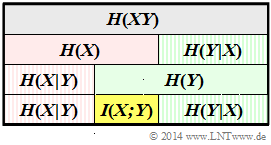
From this, the following descriptive variables can also be determined very easily according to the above scheme – shown for the random variable $XY$:
- the conditional entropies:
- $$H(X \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}\big [\log_2 P_{ X \hspace{0.05cm}|\hspace{0.05cm}Y }( X \hspace{0.05cm}|\hspace{0.05cm} Y)\big ],$$
- $$H(Y \hspace{0.05cm}|\hspace{0.05cm} X) = -{\rm E}\big [\log_2 P_{ Y \hspace{0.05cm}|\hspace{0.05cm} X }( Y \hspace{0.05cm}|\hspace{0.05cm} X)\big ],$$
- the mutual information between $X$ and $Y$:
- $$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm}.$$
Finally, verify qualitative statements regarding the second random variable $UV$ .
Hints:
- The exercise belongs to the chapter Different entropy measures of two-dimensional random variables.
- In particular, reference is made to the pages
Conditional probability and conditional entropy as well as
Mutual information between two random variables.
Questions
Solution
(1) From the given composite probability we obtain
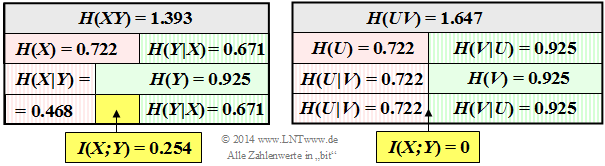
- $$H(XY) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.18} + 0.16\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.16}+ 0.02\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.02}+ 0.64\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.64} \hspace{0.15cm} \underline {= 1.393\,{\rm (bit)}} \hspace{0.05cm}.$$
(2) The one-dimensional probability functions are $P_X(X) = \big [0.2, \ 0.8 \big ]$ and $P_Y(Y) = \big [0.34, \ 0.66 \big ]$. From this follows:
- $$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.8\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.8}\hspace{0.15cm} \underline {= 0.722\,{\rm (bit)}} \hspace{0.05cm},$$
- $$H(Y) =0.34 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.34} + 0.66\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.66}\hspace{0.15cm} \underline {= 0.925\,{\rm (bit)}} \hspace{0.05cm}.$$
(3) From the graph on the information page you can see the relationship:
- $$I(X;Y) = H(X) + H(Y) - H(XY) = 0.722\,{\rm (bit)} + 0.925\,{\rm (bit)}- 1.393\,{\rm (bit)}\hspace{0.15cm} \underline {= 0.254\,{\rm (bit)}} \hspace{0.05cm}.$$
(4) Similarly, according to the graph on the information page:
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.08cm} Y) = H(XY) - H(Y) = 1.393- 0.925\hspace{0.15cm} \underline {= 0.468\,{\rm (bit)}} \hspace{0.05cm},$$
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.08cm} X) = H(XY) - H(X) = 1.393- 0.722\hspace{0.15cm} \underline {= 0.671\,{\rm (bit)}} \hspace{0.05cm}$$
- The left diagram summarises the results of subtasks (1), ... , (4) true to scale.
- The joint entropy is highlighted in grey and the mutual information in yellow.
- A red background refers to the random variable $X$, and a green one to $Y$. Hatched fields indicate a conditional entropy.
The right graph describes the same situation for the random variable $UV$ ⇒ subtask (5).
(5) According to the diagram on the right,
statements 1, 2 and 4 are correct:
- One recognises the validity of $P_{ UV } = P_U · P_V$ ⇒ mutual information $I(U; V) = 0$ by the fact that the second row of the $P_{ UV }$ matrix differs from the first row only by a constant factor $(4)$ .
- This results in the same one-dimensional probability mass functions as for the random variable $XY$ ⇒ $P_U(U) = \big [0.2, \ 0.8 \big ]$ and $P_V(V) = \big [0.34, \ 0.66 \big ]$.
- Therefore $H(U) = H(X) = 0.722\ \rm bit$ and $H(V) = H(Y) = 0.925 \ \rm bit$.
- Here, however, the following now applies for the joint entropy: $H(UV) = H(U) + H(V) ≠ H(XY)$.