Difference between revisions of "Aufgaben:Exercise 3.1: Causality Considerations"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 8: | Line 8: | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | where $f_{\rm G}$ represents the 3dB cut-off frequency: | + | where $f_{\rm G}$ represents the $\rm 3dB$ cut-off frequency: |
:$$f_{\rm G} = \frac{R}{2 \pi \cdot L} | :$$f_{\rm G} = \frac{R}{2 \pi \cdot L} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | By cascading $n$ two-port networks $H_1(f)$ built the same way, the transfer function | + | By cascading $n$ two-port networks $H_1(f)$ built in the same way, the following transfer function is obtained: |
:$$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} | :$$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} | ||
| − | \hspace{0.05cm}$$ | + | \hspace{0.05cm}.$$ |
| − | *Here, a suitable resistor decoupling is presumed, but this is not important for solving this exercise. | + | *Here, a suitable resistor decoupling is presumed, but this is not important for solving this exercise. |
*The lower graph shows for example the realization of the transfer function $H_2(f)$. | *The lower graph shows for example the realization of the transfer function $H_2(f)$. | ||
| − | In this exercise, such a two-port network is considered with respect to its causality properties. | + | In this exercise, such a two-port network is considered with respect to its causality properties. |
| − | For any causal system, the real and imaginary parts of the spectral function $H(f)$ satisfy the [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Hilbert transformation|Hilbert transformation]], which is expressed by the following abbreviation: | + | For any causal system, the real and imaginary parts of the spectral function $H(f)$ satisfy the [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Hilbert transformation|Hilbert transformation]], which is expressed by the following abbreviation: |
:$${\rm Im} \left\{ H(f) \right \} \quad | :$${\rm Im} \left\{ H(f) \right \} \quad | ||
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
{\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | ||
| − | Since the Hilbert transformation provides important information not only for transfer functions but also for time signals, the correspondence is often expressed by the general variable $x$ | + | Since the Hilbert transformation provides important information not only for transfer functions but also for time signals, the correspondence is often expressed by the general variable $x$, which is to be interpreted - depending on the application - as normalized frequency or as normalized time. |
| Line 33: | Line 33: | ||
| − | + | Please note: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem|Conclusions from the Allocation Theorem]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem|Conclusions from the Allocation Theorem]]. | ||
| − | *Reference is also made to the theory pages [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem# | + | *Reference is also made to the theory pages [[Linear_and_Time_Invariant_Systems/Conclusions_from_the_Allocation_Theorem#Hilbert_transform|Hilbert transformation]] and [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Partial fraction decomposition|Partial fraction decomposition]]. |
| Line 57: | Line 54: | ||
| − | {Compute the transfer function $H_2(f)$. What is the complex value for $f = f_{\rm G}$? | + | {Compute the transfer function $H_2(f)$. What is the complex value for $f = f_{\rm G}$? |
|type="{}"} | |type="{}"} | ||
${\rm Re}\big[H_2(f = f_{\rm G})\big] \ = \ $ { 0. } | ${\rm Re}\big[H_2(f = f_{\rm G})\big] \ = \ $ { 0. } | ||
| Line 75: | Line 72: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Proposed solution 2</u> is | + | '''(1)''' <u>Proposed solution 2</u> is correct: |
*The given transfer function can be computed according to the voltage divider principle. The following holds: | *The given transfer function can be computed according to the voltage divider principle. The following holds: | ||
:$$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$ | :$$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$ | ||
| Line 83: | Line 80: | ||
| − | '''(2)''' <u>Yes</u> is | + | '''(2)''' <u>Yes</u> is correct: |
| − | *Every real network is causal. The impulse response $h(t)$ is equal to the output signal $y(t)$ if at time $t= 0$ an extremely short impulse – a so-called Dirac impulse – is applied to the input. | + | *Every real network is causal. The impulse response $h(t)$ is equal to the output signal $y(t)$ if at time $t= 0$ an extremely short impulse – a so-called Dirac delta impulse – is applied to the input. |
| − | *Then, a signal | + | *Then, a signal cannot occur at the output already for times $t< 0$ for causality reasons: |
:$$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | :$$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | ||
t<0 \hspace{0.05cm}.$$ | t<0 \hspace{0.05cm}.$$ | ||
| − | *Formally, this can be shown as follows: The high-pass | + | *Formally, this can be shown as follows: The high-pass transfer function $H_1(f)$ can be rearranged as follows: |
:$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} | :$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} | ||
= 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} | = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
*The second transfer function describes the low-pass function equivalent to $H_1(f)$, which results in the exponential function in the time domain. | *The second transfer function describes the low-pass function equivalent to $H_1(f)$, which results in the exponential function in the time domain. | ||
| − | *The "$1$" becomes a Dirac function. Considering $T = 2\pi \cdot f_{\rm G}$ the following thus holds for $t \ge 0$: | + | *The "$1$" becomes a Dirac delta function. Considering $T = 2\pi \cdot f_{\rm G}$ the following thus holds for $t \ge 0$: |
:$$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$ | :$$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$ | ||
| − | *In contrast, $h_1(t)= 0$ holds for $t< 0$ | + | *In contrast, $h_1(t)= 0$ holds for $t< 0$, which would prove causality. |
| − | '''(3)''' | + | '''(3)''' The series connection of two high-pass filters results in the following transfer function: |
:$$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} | :$$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} | ||
=\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} | =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} | ||
| Line 106: | Line 103: | ||
{\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$ | {\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$ | ||
| − | * | + | *With $f = f_{\rm G}$ from this it follows that: |
:$$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} | :$$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} | ||
{4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} | {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} | ||
| Line 113: | Line 110: | ||
| − | '''(4)''' | + | '''(4)''' <u>The first two proposed solutions</u> are correct: |
| − | * | + | *Since the impulse response is $h_1(t) = 0$ for $t < 0$, the convolution operation $h_2(t) = h_1(t) \star h_1(t)$ also satisfies the causality condition. |
| + | *Similarly, the $n$–fold convolution yields a causal impulse response: $h_n(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} | ||
t<0 \hspace{0.05cm}.$ | t<0 \hspace{0.05cm}.$ | ||
| − | * | + | *However, the real and imaginary parts of the spectral function $H_2(f)$ are related via the Hilbert transformation for a causal impulse response $h_2(t)$ . |
| + | *Thus, considering the shortcut $x = f/f_{\rm G}$ and the result of the subtask '''(3)''' the following holds: | ||
:$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad | :$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad | ||
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
Latest revision as of 16:10, 9 October 2021
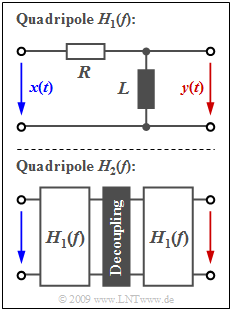
The graph shows above the two-port network with the transfer function
- $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm},$$
where $f_{\rm G}$ represents the $\rm 3dB$ cut-off frequency:
- $$f_{\rm G} = \frac{R}{2 \pi \cdot L} \hspace{0.05cm}.$$
By cascading $n$ two-port networks $H_1(f)$ built in the same way, the following transfer function is obtained:
- $$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} \hspace{0.05cm}.$$
- Here, a suitable resistor decoupling is presumed, but this is not important for solving this exercise.
- The lower graph shows for example the realization of the transfer function $H_2(f)$.
In this exercise, such a two-port network is considered with respect to its causality properties.
For any causal system, the real and imaginary parts of the spectral function $H(f)$ satisfy the Hilbert transformation, which is expressed by the following abbreviation:
- $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$
Since the Hilbert transformation provides important information not only for transfer functions but also for time signals, the correspondence is often expressed by the general variable $x$, which is to be interpreted - depending on the application - as normalized frequency or as normalized time.
Please note:
- The exercise belongs to the chapter Conclusions from the Allocation Theorem.
- Reference is also made to the theory pages Hilbert transformation and Partial fraction decomposition.
Questions
Solution
- The given transfer function can be computed according to the voltage divider principle. The following holds:
- $$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$
- This is a high-pass filter.
- For very low frequencies, the inductivity $L$ constitutes a short circuit.
(2) Yes is correct:
- Every real network is causal. The impulse response $h(t)$ is equal to the output signal $y(t)$ if at time $t= 0$ an extremely short impulse – a so-called Dirac delta impulse – is applied to the input.
- Then, a signal cannot occur at the output already for times $t< 0$ for causality reasons:
- $$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$
- Formally, this can be shown as follows: The high-pass transfer function $H_1(f)$ can be rearranged as follows:
- $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm}.$$
- The second transfer function describes the low-pass function equivalent to $H_1(f)$, which results in the exponential function in the time domain.
- The "$1$" becomes a Dirac delta function. Considering $T = 2\pi \cdot f_{\rm G}$ the following thus holds for $t \ge 0$:
- $$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$
- In contrast, $h_1(t)= 0$ holds for $t< 0$, which would prove causality.
(3) The series connection of two high-pass filters results in the following transfer function:
- $$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} {\big [(1+{\rm j}\cdot f/f_{\rm G}) \cdot (1-{\rm j}\cdot f/f_{\rm G})\big ]^2}= \frac{(f/f_{\rm G})^4 - (f/f_{\rm G})^2 +{\rm j}\cdot 2 \cdot (f/f_{\rm G})^3)} {\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$
- With $f = f_{\rm G}$ from this it follows that:
- $$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} {\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$
(4) The first two proposed solutions are correct:
- Since the impulse response is $h_1(t) = 0$ for $t < 0$, the convolution operation $h_2(t) = h_1(t) \star h_1(t)$ also satisfies the causality condition.
- Similarly, the $n$–fold convolution yields a causal impulse response: $h_n(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$
- However, the real and imaginary parts of the spectral function $H_2(f)$ are related via the Hilbert transformation for a causal impulse response $h_2(t)$ .
- Thus, considering the shortcut $x = f/f_{\rm G}$ and the result of the subtask (3) the following holds:
- $$\frac{x^4- x^2}{x^4+2 x^2+1} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{2x^3}{x^4+2 x^2+1}\hspace{0.05cm}.$$