Difference between revisions of "Aufgaben:Exercise 3.3: p-Transfer Function"
| (14 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1765__LZI_A_3_3.png|right|frame| | + | [[File:P_ID1765__LZI_A_3_3.png|right|frame|Considered two-port network]] |
| − | + | Any linear time-invariant system that can be realized by a circuit of discrete time-constant components (resistances $R$, capacitances $C$, inductances $L$, amplifier elements, etc.) is causal and has a fractional–rational $p$–transfer function of the form | |
:$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} | :$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} | ||
{B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} | {B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *All coefficients $A_Z$, ... , $A_0$, $B_N$, ... , $B_0$ are real. |
| − | *$Z$ | + | *$Z$ denotes the degree of the numerator polynomial $Z(p)$. |
| − | *$N$ | + | *$N$ denotes the degree of the denominator polynomial $N(p)$ . |
| − | + | An equivalent representation form of the above equation is: | |
:$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} | :$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} | ||
{\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{ ...} \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} | {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{ ...} \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} | ||
| Line 20: | Line 20: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | The $Z + N + 1$ parameters mean: | |
| − | * $K = A_Z/B_n$ | + | * $K = A_Z/B_n$ is a constant factor. If $Z = N$ applies, then this is dimensionless. |
| − | * | + | * The solutions of the equation $Z(p) = 0$ yield the $Z$ zeros $p_{{\rm o}1}$, ... , $p_{{\rm o}Z}$ of $H_{\rm L}(p)$. |
| − | * | + | * The zeros of the denominator polynomial $N(p)$ yield the $N$ poles $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ of the transfer function. |
| − | + | These characteristics are to be determined for the circuit shown in the diagram with the following components: | |
:$$R = 50\,\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,\,{\rm µ H}\hspace{0.05cm},\hspace{0.2cm}C = 25\,\,{\rm nF}$$ | :$$R = 50\,\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,\,{\rm µ H}\hspace{0.05cm},\hspace{0.2cm}C = 25\,\,{\rm nF}$$ | ||
| − | + | Additionally, the Fourier frequency response $H(f)$ is to be determined which arises as a result from $H_{\rm L}(p)$ by the substitution $p= {\rm j } \cdot 2\pi f$ . | |
| Line 37: | Line 37: | ||
| − | + | Please note: | |
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | ||
| − | * | + | *The following are the auxiliary quantities used in this exercise: |
:$$A = \frac{R}{2L}\hspace{0.05cm},\hspace{0.2cm} B = \frac{1}{\sqrt{LC}}\hspace{0.05cm} .$$ | :$$A = \frac{R}{2L}\hspace{0.05cm},\hspace{0.2cm} B = \frac{1}{\sqrt{LC}}\hspace{0.05cm} .$$ | ||
| Line 47: | Line 47: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the $p$–transfer function. What asymptotic values are obtained for $p → 0$ and $p → \infty$? |
|type="{}"} | |type="{}"} | ||
$H_L(p → 0) \ = \ $ { 1 3% } | $H_L(p → 0) \ = \ $ { 1 3% } | ||
| Line 53: | Line 53: | ||
| − | { | + | {Find the frequency response $H(f)$ from $H_{\rm L}(p)$ by setting $p= {\rm j } \cdot 2\pi f$ . Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It is a band-pass filter. |
| − | + | + | + It is a band-stop filter. |
| − | - | + | - Without exact knowledge of $R$, $L$ and $C$ it is not possible to make a statement. |
| − | { | + | {Compute the auxiliary quantities $A$ and $B$ for $R = 50 \ \rm \Omega$, $L = 10 \ µ\rm H$, $C = 25 \ \rm nF$. |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 2.5 3% } $\ \cdot \ 10^6 \ \rm 1/s$ | $A \ = \ $ { 2.5 3% } $\ \cdot \ 10^6 \ \rm 1/s$ | ||
| Line 66: | Line 66: | ||
| − | { | + | {Express $H_{\rm L}(p)$ in pole–zero form. How many zeros $(Z)$ and poles $(N)$ are there? What is the constant factor $K$? |
|type="{}"} | |type="{}"} | ||
$Z \ = \ $ { 2 3% } | $Z \ = \ $ { 2 3% } | ||
| Line 73: | Line 73: | ||
| − | { | + | {Compute the zeros $p_\text{o1}$ (in the upper half-plane) and $p_\text{o2}$ (in the lower half-plane). Consider the unit $\rm 1/ µs$. |
|type="{}"} | |type="{}"} | ||
${\rm Re}\{p_\text{o1}\} \ =\ $ { 0. } $\ \rm 1/ µ s$ | ${\rm Re}\{p_\text{o1}\} \ =\ $ { 0. } $\ \rm 1/ µ s$ | ||
| Line 81: | Line 81: | ||
| − | { | + | {Compute the poles $p_\text{x1}$ and $p_\text{x2}$. Let $|p_\text{x2}| > |p_\text{x1}|$ hold. |
|type="{}"} | |type="{}"} | ||
${\rm Re}\{p_\text{x1}\} \ =\ $ { -1.03--0.97 } $\ \rm 1/ µ s$ | ${\rm Re}\{p_\text{x1}\} \ =\ $ { -1.03--0.97 } $\ \rm 1/ µ s$ | ||
| Line 89: | Line 89: | ||
| − | { | + | {How can you change the position of the poles without changing the zeros? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Change of $R$; $L$ and $C$ unchanged. |
| − | - | + | - Change of $L$; $R$ and $C$ unchanged. |
| − | - | + | - Change of $C$; $L$ and $R$ unchanged. |
| − | { | + | {How must the auxiliary quantity $A$ be changed $(B$ unchanged$)$ so that a double pole occurs (critically-damped case)? |
|type="{}"} | |type="{}"} | ||
$A \ =\ $ { 2 3% } $\ \rm \cdot 10^6\ 1/s$ | $A \ =\ $ { 2 3% } $\ \rm \cdot 10^6\ 1/s$ | ||
| Line 106: | Line 106: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
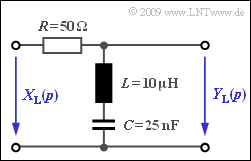
| − | '''(1)''' | + | '''(1)''' According to the voltage divider principle, the following can be written for the $p$–transfer function: |
:$$H_{\rm L}(p)= \frac {pL +{1}/{(pC)}} | :$$H_{\rm L}(p)= \frac {pL +{1}/{(pC)}} | ||
{R + pL + {1}/{(pC)}}= \frac { p^2 \cdot{LC}+1} | {R + pL + {1}/{(pC)}}= \frac { p^2 \cdot{LC}+1} | ||
| Line 112: | Line 112: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The two desired limit processes yield: |
:$$\underline {H_{\rm L}(p \rightarrow 0)= 1, \hspace{0.2cm}H_{\rm L}(p \rightarrow \infty)= 1} | :$$\underline {H_{\rm L}(p \rightarrow 0)= 1, \hspace{0.2cm}H_{\rm L}(p \rightarrow \infty)= 1} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | :# | + | :#From this it follows that it can be neither a low-pass filter nor a high-pass filter. |
| − | :# | + | :#Both at very low and very high frequencies, $y(t)=x(t)$ holds. |
| − | '''(2)''' | + | '''(2)''' <u>Suggested solution 2</u> is correct: |
| − | * | + | *Replacing $p$ by ${\rm j } \cdot 2\pi f$ the following is obtained: |
:$$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} | :$$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} | ||
{1 - (2\pi f)^2 \cdot LC + {\rm j} \cdot 2\pi f \cdot RC} | {1 - (2\pi f)^2 \cdot LC + {\rm j} \cdot 2\pi f \cdot RC} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *So, there is always a frequency at which the numerator is zero, namely the resonance frequency of $L$ and $C$. |
| − | * | + | *For this frequency $f_0 = 1 \ \rm MHz/2\pi$ the series connection of $L$ and $C$ acts like a short circuit. |
| − | * | + | *From this it follows: Regardless of the values of $R$, $L$ and $C$ it is a $\rm band–stop \:filter$. |
| − | '''(3)''' | + | '''(3)''' The following holds according to the information sheet: |
:$$A = \frac{R}{2L}= \frac{50\,{\rm \Omega}}{2 \cdot 10\,{\rm \mu H}} = \frac{50\,{\rm \Omega}}{2 \cdot 10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm} \underline {= | :$$A = \frac{R}{2L}= \frac{50\,{\rm \Omega}}{2 \cdot 10\,{\rm \mu H}} = \frac{50\,{\rm \Omega}}{2 \cdot 10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm} \underline {= | ||
2.5} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm},$$ | 2.5} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm},$$ | ||
| Line 141: | Line 141: | ||
| − | '''(4)''' | + | '''(4)''' Using $A=R/(2L)$ and $B^2 = 1/(LC)$ the following is obtained from the $p$–transfer function determined in subtask '''(1)''' : |
:$$H_{\rm L}(p)= \frac { p^2 + {1}/(LC)} | :$$H_{\rm L}(p)= \frac { p^2 + {1}/(LC)} | ||
{p^2 + p \cdot{R}/{L} +{1}/(LC)} = \frac { p^2 + B^2} | {p^2 + p \cdot{R}/{L} +{1}/(LC)} = \frac { p^2 + B^2} | ||
| Line 147: | Line 147: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The numerator polynomial $Z(p)$ and the denominator polynomial $N(p)$ are each quadratic ⇒ $\underline {Z = N = 2}$. |
| − | * | + | *The constant factor is $\underline {K = 1}$. |
| − | '''(5)''' | + | '''(5)''' Solving the equation $p^2 + B^2 = 0$ leads to the result $p = \pm {\rm j} \cdot B$ and thus to the zeros |
:$${\rm Re}\{ p_{\rm o1}\} \underline {= 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o1}\} \underline {=+2.5} \cdot 10^6 \, {1}/{{\rm | :$${\rm Re}\{ p_{\rm o1}\} \underline {= 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o1}\} \underline {=+2.5} \cdot 10^6 \, {1}/{{\rm | ||
s}} \hspace{0.05cm},$$ | s}} \hspace{0.05cm},$$ | ||
| Line 158: | Line 158: | ||
s}} \hspace{0.05cm}.$$ | s}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The normalization of the variable $p$ and all poles and zeros to the unit $( \rm 1/µ s)$ simplifies the numerical evaluation, especially in the time domain. |
| − | * | + | *If the unit is dispensed with altogether, all $t$–values are obtained in microseconds. |
| − | '''(6)''' | + | '''(6)''' If the denominator polynomial is set $N(p) = 0$, the following conditional equation arises as a result: |
:$$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} | p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} | ||
| Line 179: | Line 179: | ||
\mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm}.$$ | \mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm}.$$ | ||
| − | + | This result is only unique considering the specification $|p_\text{x2}| > |p_\text{x1}|$. | |
| − | '''(7)''' | + | '''(7)''' <u>Suggested solution 1</u> is correct: |
| − | * | + | *Since only one of the components is to be changed, $L$ and $C$ must remain the same because otherwise the zeros would also be shifted. |
| − | * | + | * The resistance value $R$ must be changed. |
| − | '''(8)''' | + | '''(8)''' According to the result in subtask '''(7)''' there is a double pole for $\underline {A = B = 2 \cdot 10^{-6} \cdot \rm 1/s}$. |
| − | * | + | *To do this, the ohmic resistance must be reduced from $50 \ \rm \Omega$ to $40 \ \rm \Omega$ . |
| − | * | + | *Then, the double pole is at ${-2 \cdot 10^{6} \cdot \rm 1/s}$. |
| − | * | + | *Or with another normalization at ${-2 \cdot \rm (1/µ s)}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 14:16, 13 October 2021
Any linear time-invariant system that can be realized by a circuit of discrete time-constant components (resistances $R$, capacitances $C$, inductances $L$, amplifier elements, etc.) is causal and has a fractional–rational $p$–transfer function of the form
- $$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} {B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$
- All coefficients $A_Z$, ... , $A_0$, $B_N$, ... , $B_0$ are real.
- $Z$ denotes the degree of the numerator polynomial $Z(p)$.
- $N$ denotes the degree of the denominator polynomial $N(p)$ .
An equivalent representation form of the above equation is:
- $$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{ ...} \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{ ...} \cdot (p - p_{{\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$
The $Z + N + 1$ parameters mean:
- $K = A_Z/B_n$ is a constant factor. If $Z = N$ applies, then this is dimensionless.
- The solutions of the equation $Z(p) = 0$ yield the $Z$ zeros $p_{{\rm o}1}$, ... , $p_{{\rm o}Z}$ of $H_{\rm L}(p)$.
- The zeros of the denominator polynomial $N(p)$ yield the $N$ poles $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ of the transfer function.
These characteristics are to be determined for the circuit shown in the diagram with the following components:
- $$R = 50\,\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,\,{\rm µ H}\hspace{0.05cm},\hspace{0.2cm}C = 25\,\,{\rm nF}$$
Additionally, the Fourier frequency response $H(f)$ is to be determined which arises as a result from $H_{\rm L}(p)$ by the substitution $p= {\rm j } \cdot 2\pi f$ .
Please note:
- The exercise belongs to the chapter Laplace Transform and p-Transfer Function.
- The following are the auxiliary quantities used in this exercise:
- $$A = \frac{R}{2L}\hspace{0.05cm},\hspace{0.2cm} B = \frac{1}{\sqrt{LC}}\hspace{0.05cm} .$$
Questions
Solution
- $$H_{\rm L}(p)= \frac {pL +{1}/{(pC)}} {R + pL + {1}/{(pC)}}= \frac { p^2 \cdot{LC}+1} {p^2 \cdot{LC} + p \cdot{RC}+ 1} \hspace{0.05cm} .$$
- The two desired limit processes yield:
- $$\underline {H_{\rm L}(p \rightarrow 0)= 1, \hspace{0.2cm}H_{\rm L}(p \rightarrow \infty)= 1} \hspace{0.05cm} .$$
- From this it follows that it can be neither a low-pass filter nor a high-pass filter.
- Both at very low and very high frequencies, $y(t)=x(t)$ holds.
(2) Suggested solution 2 is correct:
- Replacing $p$ by ${\rm j } \cdot 2\pi f$ the following is obtained:
- $$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} {1 - (2\pi f)^2 \cdot LC + {\rm j} \cdot 2\pi f \cdot RC} \hspace{0.05cm} .$$
- So, there is always a frequency at which the numerator is zero, namely the resonance frequency of $L$ and $C$.
- For this frequency $f_0 = 1 \ \rm MHz/2\pi$ the series connection of $L$ and $C$ acts like a short circuit.
- From this it follows: Regardless of the values of $R$, $L$ and $C$ it is a $\rm band–stop \:filter$.
(3) The following holds according to the information sheet:
- $$A = \frac{R}{2L}= \frac{50\,{\rm \Omega}}{2 \cdot 10\,{\rm \mu H}} = \frac{50\,{\rm \Omega}}{2 \cdot 10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm} \underline {= 2.5} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm},$$
- $$ B = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{10^{-5 }\,{\rm \Omega s} \cdot 25 \cdot 10^{-9 }\,{\rm s/\Omega }}}\hspace{0.15cm} \underline {= 2.0} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm} .$$
(4) Using $A=R/(2L)$ and $B^2 = 1/(LC)$ the following is obtained from the $p$–transfer function determined in subtask (1) :
- $$H_{\rm L}(p)= \frac { p^2 + {1}/(LC)} {p^2 + p \cdot{R}/{L} +{1}/(LC)} = \frac { p^2 + B^2} {p^2 + 2A \cdot p + B^2} \hspace{0.05cm} .$$
- The numerator polynomial $Z(p)$ and the denominator polynomial $N(p)$ are each quadratic ⇒ $\underline {Z = N = 2}$.
- The constant factor is $\underline {K = 1}$.
(5) Solving the equation $p^2 + B^2 = 0$ leads to the result $p = \pm {\rm j} \cdot B$ and thus to the zeros
- $${\rm Re}\{ p_{\rm o1}\} \underline {= 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o1}\} \underline {=+2.5} \cdot 10^6 \, {1}/{{\rm s}} \hspace{0.05cm},$$
- $$ {\rm Re}\{ p_{\rm o2}\}\hspace{0.15cm} \underline { = 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o2}\} \underline {=-2.5} \cdot 10^6 \, {1}/{{\rm s}} \hspace{0.05cm}.$$
- The normalization of the variable $p$ and all poles and zeros to the unit $( \rm 1/µ s)$ simplifies the numerical evaluation, especially in the time domain.
- If the unit is dispensed with altogether, all $t$–values are obtained in microseconds.
(6) If the denominator polynomial is set $N(p) = 0$, the following conditional equation arises as a result:
- $$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} \hspace{0.05cm},$$
- $${\rm Mit}\hspace{0.2cm}A = 2.5 \cdot 10^6 \cdot {1}/{\rm s}\hspace{0.05cm},\hspace{0.2cm} \sqrt{A^2 - B^2}= 1.5 \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.05cm}:$$
- $${\rm Re}\{ p_{\rm x1}\}\hspace{0.15cm} \underline {= -1} \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.15cm} \underline {= -1} \cdot {1}/{{\rm \mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm},$$
- $${\rm Re}\{ p_{\rm x2}\}\hspace{0.15cm} \underline {= -4} \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.15cm} \underline {= -4} \cdot {1}/{{\rm \mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm}.$$
This result is only unique considering the specification $|p_\text{x2}| > |p_\text{x1}|$.
(7) Suggested solution 1 is correct:
- Since only one of the components is to be changed, $L$ and $C$ must remain the same because otherwise the zeros would also be shifted.
- The resistance value $R$ must be changed.
(8) According to the result in subtask (7) there is a double pole for $\underline {A = B = 2 \cdot 10^{-6} \cdot \rm 1/s}$.
- To do this, the ohmic resistance must be reduced from $50 \ \rm \Omega$ to $40 \ \rm \Omega$ .
- Then, the double pole is at ${-2 \cdot 10^{6} \cdot \rm 1/s}$.
- Or with another normalization at ${-2 \cdot \rm (1/µ s)}$.