Difference between revisions of "Aufgaben:Exercise 3.3: p-Transfer Function"
| (One intermediate revision by the same user not shown) | |||
| Line 4: | Line 4: | ||
[[File:P_ID1765__LZI_A_3_3.png|right|frame|Considered two-port network]] | [[File:P_ID1765__LZI_A_3_3.png|right|frame|Considered two-port network]] | ||
| − | Any linear time-invariant system that can be realized by a circuit of discrete time-constant components (resistances $R$, capacitances $C$, inductances $L$, amplifier elements, etc.) is causal and | + | Any linear time-invariant system that can be realized by a circuit of discrete time-constant components (resistances $R$, capacitances $C$, inductances $L$, amplifier elements, etc.) is causal and has a fractional–rational $p$–transfer function of the form |
:$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} | :$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} | ||
{B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} | {B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} | ||
| Line 21: | Line 21: | ||
The $Z + N + 1$ parameters mean: | The $Z + N + 1$ parameters mean: | ||
| − | * $K = A_Z/B_n$ is a constant factor. If $Z = N$ applies, then this is dimensionless. | + | * $K = A_Z/B_n$ is a constant factor. If $Z = N$ applies, then this is dimensionless. |
| − | * The solutions of the equation $Z(p) = 0$ yield the $Z$ zeros $p_{{\rm o}1}$, ... , $p_{{\rm o} | + | * The solutions of the equation $Z(p) = 0$ yield the $Z$ zeros $p_{{\rm o}1}$, ... , $p_{{\rm o}Z}$ of $H_{\rm L}(p)$. |
* The zeros of the denominator polynomial $N(p)$ yield the $N$ poles $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ of the transfer function. | * The zeros of the denominator polynomial $N(p)$ yield the $N$ poles $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ of the transfer function. | ||
| Line 37: | Line 37: | ||
| − | + | Please note: | |
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function|Laplace Transform and p-Transfer Function]]. | ||
| Line 121: | Line 121: | ||
| − | '''(2)''' <u>Suggested solution 2</u> is correct: | + | '''(2)''' <u>Suggested solution 2</u> is correct: |
*Replacing $p$ by ${\rm j } \cdot 2\pi f$ the following is obtained: | *Replacing $p$ by ${\rm j } \cdot 2\pi f$ the following is obtained: | ||
:$$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} | :$$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} | ||
| Line 127: | Line 127: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | *So, there is always a frequency at which the numerator is zero, namely the resonance frequency of $L$ and $C$. | + | *So, there is always a frequency at which the numerator is zero, namely the resonance frequency of $L$ and $C$. |
*For this frequency $f_0 = 1 \ \rm MHz/2\pi$ the series connection of $L$ and $C$ acts like a short circuit. | *For this frequency $f_0 = 1 \ \rm MHz/2\pi$ the series connection of $L$ and $C$ acts like a short circuit. | ||
| − | *From this it follows: Regardless of the values of $R$, $L$ and $C$ it is a $\rm band–stop \:filter$. | + | *From this it follows: Regardless of the values of $R$, $L$ and $C$ it is a $\rm band–stop \:filter$. |
| Line 158: | Line 158: | ||
s}} \hspace{0.05cm}.$$ | s}} \hspace{0.05cm}.$$ | ||
| − | *The normalization of the variable $p$ and all poles and zeros to the unit $( \rm 1/µ s)$ simplifies the numerical evaluation, especially in the time domain. | + | *The normalization of the variable $p$ and all poles and zeros to the unit $( \rm 1/µ s)$ simplifies the numerical evaluation, especially in the time domain. |
| − | *If the unit is dispensed with altogether, all $t$–values are obtained in microseconds. | + | *If the unit is dispensed with altogether, all $t$–values are obtained in microseconds. |
| − | '''(6)''' If the denominator polynomial is set $N(p) = 0$, the following conditional equation arises as a result: | + | '''(6)''' If the denominator polynomial is set $N(p) = 0$, the following conditional equation arises as a result: |
:$$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} | p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} | ||
| Line 183: | Line 183: | ||
| − | '''(7)''' <u>Suggested solution 1</u> is correct: | + | '''(7)''' <u>Suggested solution 1</u> is correct: |
*Since only one of the components is to be changed, $L$ and $C$ must remain the same because otherwise the zeros would also be shifted. | *Since only one of the components is to be changed, $L$ and $C$ must remain the same because otherwise the zeros would also be shifted. | ||
* The resistance value $R$ must be changed. | * The resistance value $R$ must be changed. | ||
| Line 190: | Line 190: | ||
'''(8)''' According to the result in subtask '''(7)''' there is a double pole for $\underline {A = B = 2 \cdot 10^{-6} \cdot \rm 1/s}$. | '''(8)''' According to the result in subtask '''(7)''' there is a double pole for $\underline {A = B = 2 \cdot 10^{-6} \cdot \rm 1/s}$. | ||
| − | *To do this, the ohmic resistance must be reduced from $50 \ \rm \Omega$ to $40 \ \rm \Omega$ . | + | *To do this, the ohmic resistance must be reduced from $50 \ \rm \Omega$ to $40 \ \rm \Omega$ . |
| − | *Then, the double pole is at ${-2 \cdot 10^{6} \cdot \rm 1/s}$. | + | *Then, the double pole is at ${-2 \cdot 10^{6} \cdot \rm 1/s}$. |
*Or with another normalization at ${-2 \cdot \rm (1/µ s)}$. | *Or with another normalization at ${-2 \cdot \rm (1/µ s)}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 14:16, 13 October 2021
Any linear time-invariant system that can be realized by a circuit of discrete time-constant components (resistances $R$, capacitances $C$, inductances $L$, amplifier elements, etc.) is causal and has a fractional–rational $p$–transfer function of the form
- $$H_{\rm L}(p)= \frac {A_Z \cdot p^Z +\text{ ...} + A_1 \cdot p + A_0} {B_N \cdot p^N + \text{ ...} + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$
- All coefficients $A_Z$, ... , $A_0$, $B_N$, ... , $B_0$ are real.
- $Z$ denotes the degree of the numerator polynomial $Z(p)$.
- $N$ denotes the degree of the denominator polynomial $N(p)$ .
An equivalent representation form of the above equation is:
- $$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot \text{ ...} \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot \text{ ...} \cdot (p - p_{{\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$
The $Z + N + 1$ parameters mean:
- $K = A_Z/B_n$ is a constant factor. If $Z = N$ applies, then this is dimensionless.
- The solutions of the equation $Z(p) = 0$ yield the $Z$ zeros $p_{{\rm o}1}$, ... , $p_{{\rm o}Z}$ of $H_{\rm L}(p)$.
- The zeros of the denominator polynomial $N(p)$ yield the $N$ poles $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ of the transfer function.
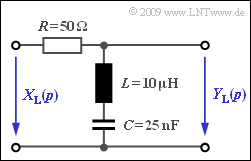
These characteristics are to be determined for the circuit shown in the diagram with the following components:
- $$R = 50\,\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,\,{\rm µ H}\hspace{0.05cm},\hspace{0.2cm}C = 25\,\,{\rm nF}$$
Additionally, the Fourier frequency response $H(f)$ is to be determined which arises as a result from $H_{\rm L}(p)$ by the substitution $p= {\rm j } \cdot 2\pi f$ .
Please note:
- The exercise belongs to the chapter Laplace Transform and p-Transfer Function.
- The following are the auxiliary quantities used in this exercise:
- $$A = \frac{R}{2L}\hspace{0.05cm},\hspace{0.2cm} B = \frac{1}{\sqrt{LC}}\hspace{0.05cm} .$$
Questions
Solution
- $$H_{\rm L}(p)= \frac {pL +{1}/{(pC)}} {R + pL + {1}/{(pC)}}= \frac { p^2 \cdot{LC}+1} {p^2 \cdot{LC} + p \cdot{RC}+ 1} \hspace{0.05cm} .$$
- The two desired limit processes yield:
- $$\underline {H_{\rm L}(p \rightarrow 0)= 1, \hspace{0.2cm}H_{\rm L}(p \rightarrow \infty)= 1} \hspace{0.05cm} .$$
- From this it follows that it can be neither a low-pass filter nor a high-pass filter.
- Both at very low and very high frequencies, $y(t)=x(t)$ holds.
(2) Suggested solution 2 is correct:
- Replacing $p$ by ${\rm j } \cdot 2\pi f$ the following is obtained:
- $$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} {1 - (2\pi f)^2 \cdot LC + {\rm j} \cdot 2\pi f \cdot RC} \hspace{0.05cm} .$$
- So, there is always a frequency at which the numerator is zero, namely the resonance frequency of $L$ and $C$.
- For this frequency $f_0 = 1 \ \rm MHz/2\pi$ the series connection of $L$ and $C$ acts like a short circuit.
- From this it follows: Regardless of the values of $R$, $L$ and $C$ it is a $\rm band–stop \:filter$.
(3) The following holds according to the information sheet:
- $$A = \frac{R}{2L}= \frac{50\,{\rm \Omega}}{2 \cdot 10\,{\rm \mu H}} = \frac{50\,{\rm \Omega}}{2 \cdot 10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm} \underline {= 2.5} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm},$$
- $$ B = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{10^{-5 }\,{\rm \Omega s} \cdot 25 \cdot 10^{-9 }\,{\rm s/\Omega }}}\hspace{0.15cm} \underline {= 2.0} \cdot 10^6 \, \,{1}/{\rm s}\hspace{0.05cm} .$$
(4) Using $A=R/(2L)$ and $B^2 = 1/(LC)$ the following is obtained from the $p$–transfer function determined in subtask (1) :
- $$H_{\rm L}(p)= \frac { p^2 + {1}/(LC)} {p^2 + p \cdot{R}/{L} +{1}/(LC)} = \frac { p^2 + B^2} {p^2 + 2A \cdot p + B^2} \hspace{0.05cm} .$$
- The numerator polynomial $Z(p)$ and the denominator polynomial $N(p)$ are each quadratic ⇒ $\underline {Z = N = 2}$.
- The constant factor is $\underline {K = 1}$.
(5) Solving the equation $p^2 + B^2 = 0$ leads to the result $p = \pm {\rm j} \cdot B$ and thus to the zeros
- $${\rm Re}\{ p_{\rm o1}\} \underline {= 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o1}\} \underline {=+2.5} \cdot 10^6 \, {1}/{{\rm s}} \hspace{0.05cm},$$
- $$ {\rm Re}\{ p_{\rm o2}\}\hspace{0.15cm} \underline { = 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o2}\} \underline {=-2.5} \cdot 10^6 \, {1}/{{\rm s}} \hspace{0.05cm}.$$
- The normalization of the variable $p$ and all poles and zeros to the unit $( \rm 1/µ s)$ simplifies the numerical evaluation, especially in the time domain.
- If the unit is dispensed with altogether, all $t$–values are obtained in microseconds.
(6) If the denominator polynomial is set $N(p) = 0$, the following conditional equation arises as a result:
- $$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} \hspace{0.05cm},$$
- $${\rm Mit}\hspace{0.2cm}A = 2.5 \cdot 10^6 \cdot {1}/{\rm s}\hspace{0.05cm},\hspace{0.2cm} \sqrt{A^2 - B^2}= 1.5 \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.05cm}:$$
- $${\rm Re}\{ p_{\rm x1}\}\hspace{0.15cm} \underline {= -1} \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.15cm} \underline {= -1} \cdot {1}/{{\rm \mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm},$$
- $${\rm Re}\{ p_{\rm x2}\}\hspace{0.15cm} \underline {= -4} \cdot 10^6 \cdot {1}/{{\rm s}}\hspace{0.15cm} \underline {= -4} \cdot {1}/{{\rm \mu s}}, \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm}.$$
This result is only unique considering the specification $|p_\text{x2}| > |p_\text{x1}|$.
(7) Suggested solution 1 is correct:
- Since only one of the components is to be changed, $L$ and $C$ must remain the same because otherwise the zeros would also be shifted.
- The resistance value $R$ must be changed.
(8) According to the result in subtask (7) there is a double pole for $\underline {A = B = 2 \cdot 10^{-6} \cdot \rm 1/s}$.
- To do this, the ohmic resistance must be reduced from $50 \ \rm \Omega$ to $40 \ \rm \Omega$ .
- Then, the double pole is at ${-2 \cdot 10^{6} \cdot \rm 1/s}$.
- Or with another normalization at ${-2 \cdot \rm (1/µ s)}$.